Welcome to an exciting journey into the world of exponents! In this comprehensive guide, we will explore the concept of adding exponents. Whether you’re a student looking to excel in math, a parent seeking to support your child’s learning, or a teacher searching for effective teaching strategies, this article will provide you with the knowledge and tools you need to understand and master adding exponents.
An Introduction to Adding Exponents
Exponents, also known as powers or indices, are a fundamental concept in mathematics. They represent the number of times a base number is multiplied by itself. Adding exponents involves combining exponential expressions to find their sum. By understanding the rules and methods of adding exponents, you can simplify complex calculations and solve equations more efficiently.
What is Adding Exponents?
Adding exponents does not mean adding the exponents themselves. Instead, it is the process of adding the results of base numbers raised to their respective exponents. When the bases and exponents are identical, the process involves multiplying the base numbers. For example, when adding 2³ + 2⁴, the exponents 3 and 4 are not added. Instead, the results of 2³ and 2⁴ are added.
For those delving into the nuances of adding exponents, our exponent rules page serves as an indispensable guide. It provides comprehensive insights into fundamental rules governing exponents, offering valuable knowledge that enriches the understanding of exponentiation and its applications.
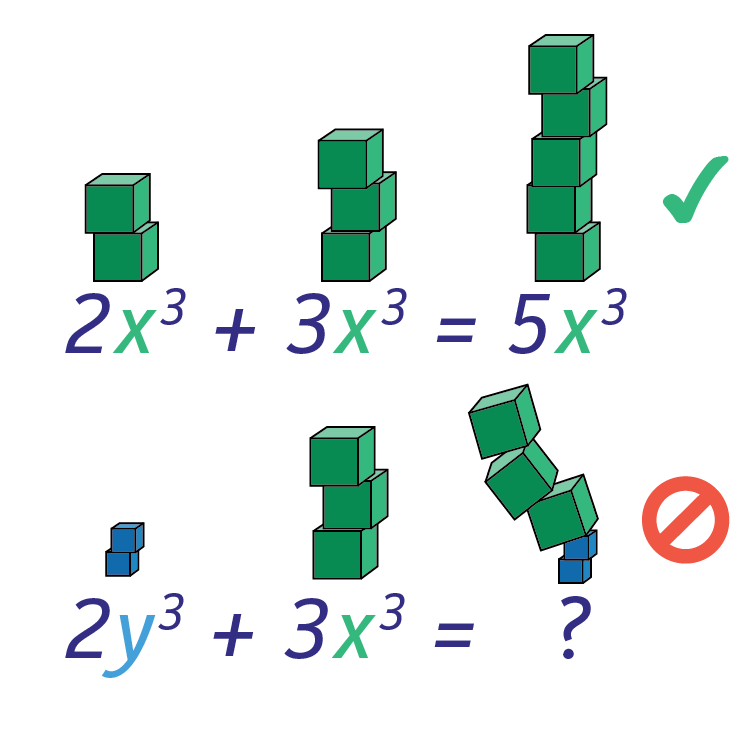
Adding Exponents Step by Step
To add exponents, there are certain steps that need to be followed. These steps vary depending on whether the base numbers and exponents are the same or different.
Step 1: Check for Same Base and Exponents
The first step in adding exponents is to check if the base numbers and exponents are the same. If they are, you can directly add the coefficients of the exponential expressions while keeping the base and exponent unchanged. For example, in the expression 2³ + 2³, both the base number (2) and the exponent (3) are the same.
Step 2: Calculate Individual Terms for Different Base and Exponents
If the base numbers and exponents are different, you need to calculate the individual terms separately before adding them together. Each base is raised to its respective exponent, and the results are added. For example, in the expression 3² + 4³, the base number (3 and 4) and exponent (2 and 3) are different.
Step 3: Add the Results
Finally, add the results obtained from Step 1 or Step 2 together to find the sum of the exponential expressions. This will give you the final answer. For example, in the expression 2³ + 2³, the sum of the two terms is 2(2³), which simplifies to 2⁴ or 16.
Adding Exponents Methods
Adding exponents can be performed using different methods, depending on the nature of the expressions being added. Here are some common methods used in adding exponents:
Adding Exponents With Same Base and Exponents
When the bases and exponents are the same, the addition is quite straightforward. The base remains the same, but the exponents are added. This process is represented as bn + bn = 2bn.
For instance, consider 4² + 4². Here, since the base (4) and the exponent (2) are the same for both terms, the result would be 2(4²) = 2 * 4 * 4 = 32.
Adding Exponents With Different Base and Exponents
When the bases and exponents are different, each term needs to be calculated separately. The general form for such expressions is an + bm.
Consider the example 4² + 2⁵. Here, each term is calculated first: 4² = 16, and 2⁵ = 32. The results are then added together to give 16 + 32 = 48.
Adding Negative Exponents With Different Bases
The process of adding negative exponents involves calculating each term separately, then adding the results. The general form for this process is a^-n + b^-m = 1/an + 1/bm.
For instance, consider 4^-2 + 2^-5. The result would be 1/4² + 1/2⁵ = 1/16 + 1/32 = 0.09375.
Adding Fractional Exponents With Same Base and Exponents
Fractional exponents can also be added when the bases and exponents are the same. The general form for this process is bn/m + bn/m = 2bn/m.
Consider the example 4²/3 + 4²/3. Here, the result would be 2(4²/3) = 2 * (³√(4²)) = 5.04.
Adding Fractional Exponents With Different Base and Exponents
When fractional exponents have different bases and exponents, each term is calculated first, then the results are added together. The general form for this process is an/m + bk/j.
Consider the example 3³/2 + 2⁵/2. Here, the result would be √(3³) + √(2⁵) = √(27) + √(32) = 5.196 + 5.657 = 10.853.
Adding Variable With Same Exponents
The process of adding variables with the same exponents is similar to adding exponents with the same base and exponents. The general form for this process is xn + xn = 2xn.
For instance, consider x² + x². Here, the result would be 2x².
Adding Variable With Different Exponents
When variables have different exponents, each term needs to be calculated separately. The general form for this process is xn + xm.
Solved Examples of Adding Exponents
To further illustrate the process of adding exponents, let’s look at some solved examples:
- Consider the expression 3³ + 3². Here, since the bases are the same (3), calculate each term separately: 3³ = 27, 3² = 9. Then add the results: 27 + 9 = 36.
- Consider the expression 2³ + 3². Here the bases are different (2 and 3). So, calculate each part separately: 2³ = 8, 3² = 9. Then add the results: 8 + 9 = 17.
How Kunduz Can Help You Learn Adding Exponents?
At Kunduz, we are committed to providing a comprehensive and engaging learning experience for students of all ages. Our expert tutors are skilled in teaching math concepts, including adding exponents, and can assist you in mastering this topic. Whether you need one-on-one tutoring, practice problems, or step-by-step explanations, Kunduz is here to support your academic journey. With our affordable and accessible services, you can enhance your math skills and achieve your academic goals.
