In mathematics, the concept of additive inverse plays a crucial role. It refers to the value that, when added to a given number, results in a sum of zero. The additive inverse is also known as the opposite or negation of a number. It is the value that nullifies the original number.
The concept of additive inverse can be easily understood by considering the number line. For any given number, its additive inverse will be located on the opposite side of the number line, equidistant from zero. When the original number and its additive inverse are added together, the result is always zero.
Opposite or Additive Inverse of a Number
The opposite or additive inverse of a number is obtained by changing the sign of the original number. If the original number is positive, its opposite will be negative, and vice versa. For example, the opposite of 5 is -5, and the opposite of -7 is 7. The sum of a number and its opposite is always zero.
What is Additive Inverse?
Additive inverse is the value that, when added to a number, yields a sum of zero. It is the opposite or negation of the original number. The additive inverse of a number is denoted by a negative sign (-) followed by the number. For example, the additive inverse of 10 is -10, and the additive inverse of -3 is 3. The concept of additive inverse is applicable to all types of numbers, including natural numbers, whole numbers, integers, fractions, decimals, and complex numbers.

How to Find the Additive inverse?
Finding the additive inverse of a number is simple. To find the additive inverse of a positive number, change the sign of the number to negative. For example, the additive inverse of 6 is -6. To find the additive inverse of a negative number, change the sign of the number to positive. For example, the additive inverse of -8 is 8. In both cases, the absolute value of the original number remains the same.
Additive Inverse Formula
The formula for finding the additive inverse of a number is straightforward. The additive inverse of a number can be obtained by multiplying the number by -1. Mathematically, the formula for finding the additive inverse of a number ‘a’ is:
Additive Inverse of a = -1 * a
For example, the additive inverse of 7 can be found by multiplying -1 with 7, resulting in -7.
Properties of Additive inverse
The additive inverse possesses several properties that make it an essential concept in mathematics. These properties include:
- Negation Property: The additive inverse of the additive inverse of a number is equal to the original number. In other words, if ‘a’ is a number, then the additive inverse of -a is a.
- Zero Property: The additive inverse of zero is zero itself. When zero is added to its additive inverse, the sum is zero.
- Commutative Property: The order of addition does not affect the result. For any two numbers ‘a’ and ‘b’, the sum of their additive inverses is equal to the additive inverse of their sum. Mathematically, (-a) + (-b) = -(a + b).
- Associative Property: The grouping of numbers does not affect the result. For any three numbers ‘a’, ‘b’, and ‘c’, the sum of their additive inverses is equal to the additive inverse of their sum. Mathematically, (-a) + [(-b) + (-c)] = -[(a + b) + c].
- Distributive Property: The additive inverse distributes over addition. For any three numbers ‘a’, ‘b’, and ‘c’, the sum of the additive inverse of ‘a’ with the product of ‘b’ and ‘c’ is equal to the product of the additive inverse of ‘a’ with ‘b’ and the additive inverse of ‘a’ with ‘c’. Mathematically, (-a) * (b + c) = (-a) * b + (-a) * c.
Additive Inverse of Real Numbers
The concept of additive inverse is applicable to real numbers, including natural numbers, whole numbers, integers, fractions, decimals, and irrational numbers. The additive inverse of real numbers is simply the negative of the given number. Let’s explore the additive inverse of different types of real numbers.
Additive inverse of Natural or Whole Numbers
Natural numbers are positive integers, starting from 1. Whole numbers include zero along with natural numbers. The additive inverse of positive natural or whole numbers will be negative, while the additive inverse of zero is zero itself.
| Whole numbers/Natural numbers | Additive Inverse | Result |
|---|---|---|
| 0 | 0 | 0 + 0 = 0 |
| 1 | -1 | 1 + (-1) = 0 |
| 2 | -2 | 2 + (-2) = 0 |
| 3 | -3 | 3 + (-3) = 0 |
| 4 | -4 | 4 + (-4) = 0 |
| 5 | -5 | 5 + (-5) = 0 |
| 10 | -10 | 10 + (-10) = 0 |
| 20 | -20 | 20 + (-20) = 0 |
| 50 | -50 | 50 + (-50) = 0 |
| 100 | -100 | 100 + (-100) = 0 |
Additive Inverse of Rational Numbers
Rational numbers are numbers that can be expressed as a fraction, where the numerator and denominator are integers. The additive inverse of a rational number is obtained by changing the sign of the numerator. For example, the additive inverse of 2/3 is -2/3.
Additive Inverse of Integers
Integers include both positive and negative whole numbers, along with zero. The additive inverse of positive integers is obtained by changing the sign of the number. For example, the additive inverse of 5 is -5. The additive inverse of negative integers is obtained by changing the sign to positive. For example, the additive inverse of -8 is 8.
Additive Inverse of a Decimal
Decimals are numbers that include a whole part and a fractional part separated by a decimal point. The additive inverse of a decimal is obtained by changing the sign of the whole part. For example, the additive inverse of 2.75 is -2.75.
Additive Inverse of Irrational Numbers
Irrational numbers are numbers that cannot be expressed as a fraction or ratio of two integers. They include non-terminating and non-repeating decimals, along with square roots and cube roots of non-perfect squares and cubes. The additive inverse of an irrational number is obtained by changing the sign of the number. For example, the additive inverse of √2 is -√2.
Additive Inverse of Complex Numbers
Complex numbers are numbers that include a real part and an imaginary part. A complex number is represented as a + bi, where a is the real part and bi is the imaginary part. The additive inverse of a complex number is obtained by changing the sign of both the real and imaginary parts. For example, the additive inverse of 3 + 4i is -3 – 4i.
Difference Between Additive Inverse and Multiplicative Inverse
Additive inverse and multiplicative inverse are two different concepts in mathematics. The additive inverse refers to the value that, when added to a given number, results in zero. On the other hand, the multiplicative inverse refers to the value that, when multiplied by a given number, results in one.
| Property | Additive Inverse | Multiplicative Inverse |
|---|---|---|
| Operation | Addition | Multiplication |
| Result | Zero | One |
| Calculation Method | Change the sign of the number | Take the reciprocal of the number |
| Example | The additive inverse of 5 is -5 | The multiplicative inverse of 5 is 1/5 |
| Mathematical Symbol | (-a) | 1/a |
| Property | The additive inverse of the additive inverse of a number is equal to the original number | The multiplicative inverse of the multiplicative inverse of a number is equal to the original number |
| Example | The additive inverse of the additive inverse of 7 is 7 | The multiplicative inverse of the multiplicative inverse of 7 is 7 |
| Application | Used to nullify the effect of addition, making the sum zero | Used to nullify the effect of multiplication, making the product one |
Additive Inverse in Algebraic Expressions
The concept of additive inverse can be extended to algebraic expressions as well. In algebra, variables and constants are combined using addition and subtraction operations. The additive inverse of an algebraic expression is obtained by changing the sign of the expression.
For example, consider the algebraic expression 2x + 3y. The additive inverse of this expression will be -(2x + 3y), which can be simplified as -2x – 3y. The sum of the original expression and its additive inverse is equal to zero.
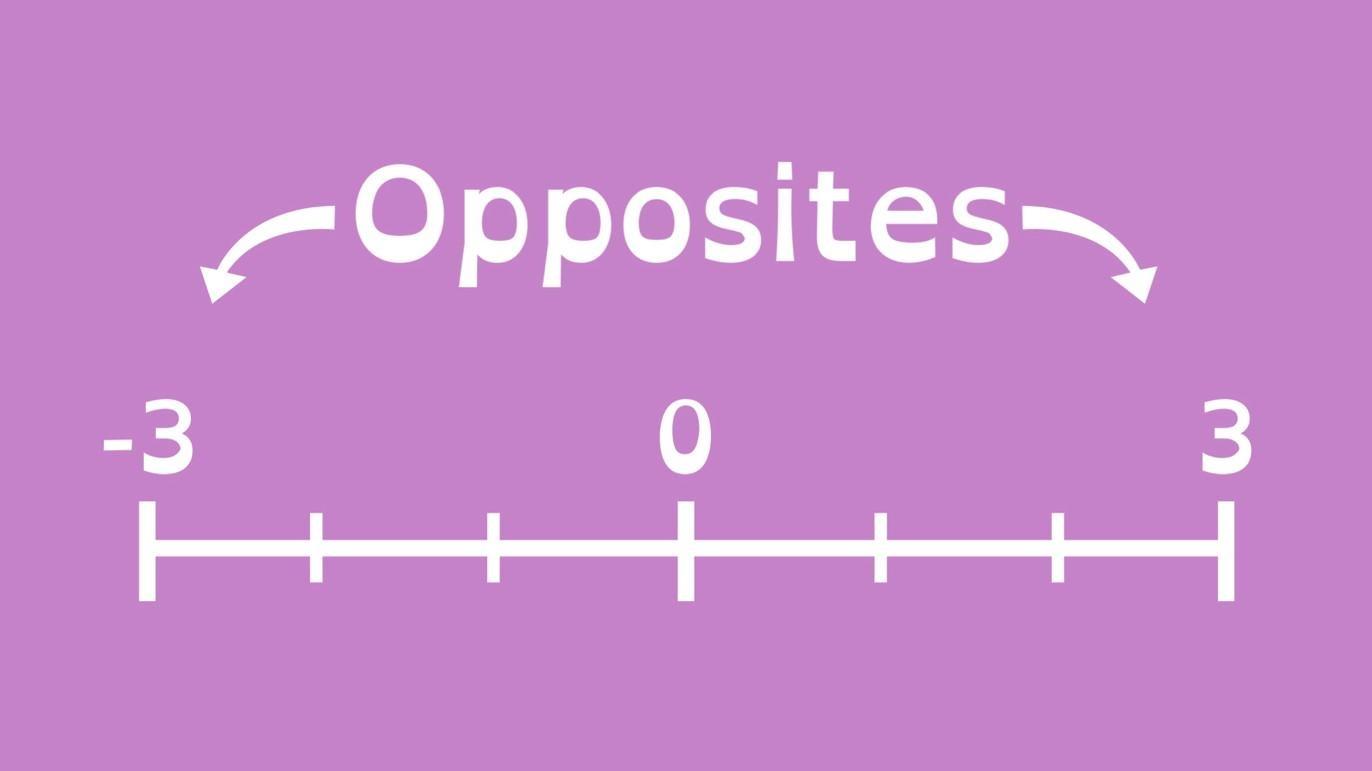
Additive Inverse on a Number Line
The concept of additive inverse can be visualized on a number line. A number line represents the set of real numbers, with positive numbers to the right of zero and negative numbers to the left of zero. The additive inverse of a number is located on the opposite side of the number line, equidistant from zero.
For example, consider the number line with zero at the center. The number 5 is represented to the right of zero, and its additive inverse, -5, is located to the left of zero, at the same distance. When 5 and -5 are added together, their sum is zero.
Solved Examples on Additive Inverse
Let’s solve some examples to better understand the concept of additive inverse.
Example 1: Find the additive inverse of 8.
Solution: The additive inverse of 8 is -8, as 8 + (-8) = 0.
Example 2: What is the additive inverse of -15?
Solution: The additive inverse of -15 is 15, as -15 + 15 = 0.
Example 3: Find the additive inverse of 3/4.
Solution: The additive inverse of 3/4 is -3/4, as 3/4 + (-3/4) = 0.
Example 4: What is the additive inverse of -2.5?
Solution: The additive inverse of -2.5 is 2.5, as -2.5 + 2.5 = 0.
How Kunduz Can Help You Learn Additive Inverse?
At Kunduz, we understand the importance of a solid foundation in mathematics. Our mission is to provide comprehensive and effective learning resources to help students excel in their mathematical journey. Whether you’re struggling with the concept of additive inverse or seeking additional practice, Kunduz can assist you.
Our online platform offers a wide range of educational materials, including interactive lessons, practice exercises, and expert guidance. With Kunduz, you can learn at your own pace and receive personalized support to enhance your understanding of additive inverse and other mathematical concepts.
Join Kunduz today and embark on a successful mathematical journey!
