Algebraic expressions play a fundamental role in mathematics, serving as a bridge between numbers and variables. These expressions allow us to represent mathematical relationships and solve complex problems. Whether you’re a student or a math enthusiast, understanding algebraic expressions is essential for mastering higher-level math concepts.
In this article, we will explore the basics of algebraic expressions, including their definition, components, operations, and various types. We will also delve into the process of evaluating algebraic expressions and provide examples to illustrate these concepts. So, let’s dive into the world of algebraic expressions and unlock the power of mathematical reasoning!
What are Algebraic Expressions?
An algebraic expression is a mathematical phrase that consists of variables, constants, coefficients, and algebraic operations. It represents a mathematical relationship or a rule that can be applied to different values of the variables. Algebraic expressions are commonly used in mathematics to model real-world problems, solve equations, and simplify complex calculations.
Let’s take a look at a simple example of an algebraic expression:
3x + 4y - 7
In this expression, x and y are variables, while 3, 4, and 7 are constants. The coefficients are the numbers multiplied by the variables (3 and 4 in this case), and the algebraic operations are addition and subtraction.
Algebraic expressions can be as simple as a single term or as complex as a combination of multiple terms. They serve as building blocks for more advanced mathematical concepts such as equations, inequalities, and polynomials.
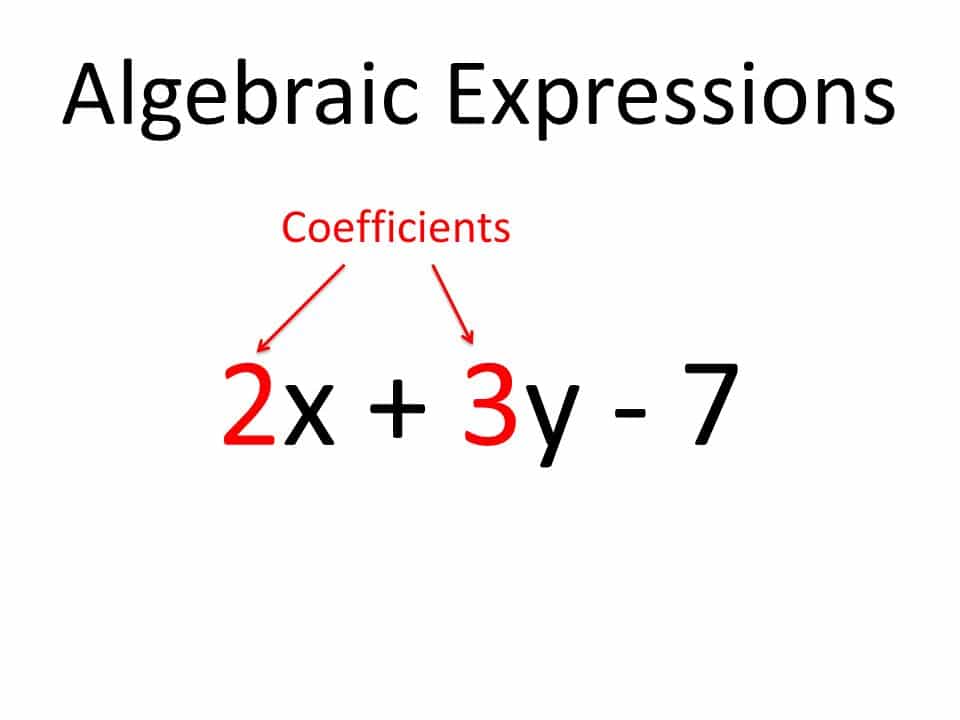
Parts of Algebraic Expressions
To understand algebraic expressions fully, let’s break them down into their components. The main parts of an algebraic expression are:
- Variables: Variables are symbols or letters that represent unknown quantities. They can take on different values in mathematical equations or expressions. Common examples of variables include
x,y, andz. - Constants: Constants are fixed values that do not change. They can be whole numbers, fractions, or even irrational numbers such as
πore. In the expression3x + 4y - 7,3,4, and7are constants. - Coefficients: Coefficients are the numbers multiplied by variables in an expression. They indicate the scale or magnitude of the variable. In the expression
3x + 4y - 7,3and4are coefficients. - Terms: Terms are the building blocks of an algebraic expression. A term can be a variable alone, a constant alone, or a combination of variables and constants multiplied or divided by each other. In the expression
3x + 4y - 7,3x,4y, and-7are the terms. - Operations: Operations such as addition (+), subtraction (-), multiplication (×), and division (÷) are used to combine terms and perform mathematical calculations within an algebraic expression.
Understanding these components is crucial for simplifying algebraic expressions, solving equations, and manipulating mathematical formulas.
Variables, Coefficients & Constants in Algebraic Expressions
In algebraic expressions, variables, coefficients, and constants play distinct roles. Let’s take a closer look at each of these components:
- Variables: Variables are symbols or letters that represent unknown quantities or values that can change. They are used to generalize mathematical relationships and solve equations. Variables can take on various values, and their purpose is to provide a flexible representation of mathematical concepts. Common variables include
x,y,z,a,b, andc. - Coefficients: Coefficients are the numbers multiplied by variables in an algebraic expression. They indicate the scale or magnitude of the variable. For example, in the expression
3x,3is the coefficient ofx. Coefficients can be positive, negative, or even fractions or decimals. - Constants: Constants are fixed values that do not change. They can be whole numbers, fractions, or even irrational numbers such as
πore. In the expression4y - 7,4and-7are constants. Constants provide a fixed reference point in mathematical calculations.
Understanding the distinction between variables, coefficients, and constants is essential for solving equations, simplifying expressions, and generalizing mathematical relationships.
Operations on Algebraic Expressions
Algebraic expressions involve various operations to combine terms and perform mathematical calculations. The main operations used in algebraic expressions are addition, subtraction, multiplication, and division. Let’s explore each operation in detail:
- Addition: Addition is the operation used to combine like terms or terms with the same variable parts. When adding algebraic expressions, you can add the coefficients of like terms while keeping the variable parts unchanged. For example, to simplify
3x + 4x, you can add the coefficients3and4to get7x. - Subtraction: Subtraction is the operation used to subtract one algebraic expression from another. To subtract algebraic expressions, you can apply the distributive property and combine like terms. For example, to simplify
5x - (2x + 3), you can distribute the negative sign and combine like terms to get5x - 2x - 3. - Multiplication: Multiplication is the operation used to multiply terms within an algebraic expression. When multiplying algebraic expressions, you can apply the distributive property and combine like terms. For example, to simplify
(2x + 3)(4x - 5), you can use the distributive property to expand the expression and then combine like terms. - Division: Division is the operation used to divide one algebraic expression by another. To divide algebraic expressions, you can factor and cancel out common terms. For example, to simplify
(6x² - 12x) / 3x, you can factor out3xfrom the numerator and denominator and then cancel out the common term to get2x - 4.
These operations allow us to manipulate algebraic expressions, simplify complex equations, and solve mathematical problems. By understanding how these operations work, you can effectively perform calculations and derive meaningful conclusions from algebraic expressions.
What is an Algebraic Equation?
An algebraic equation is a mathematical statement that involves an equality between two algebraic expressions. It represents a relationship or a rule that holds true for specific values of the variables. Algebraic equations are commonly used to solve problems and find the unknown values or variables.
In an algebraic equation, the left-hand side (LHS) is equal to the right-hand side (RHS). The equality sign (=) indicates that the expressions on both sides of the equation are equivalent. For example, the equation 2x + 3 = 7 states that the sum of 2x and 3 is equal to 7.
Solving algebraic equations involves finding the values of the variables that satisfy the equation. This can be done by applying various algebraic techniques such as simplification, factoring, expanding, and isolating the variable. The solution to an equation is the set of values that make the equation true.
Algebraic equations are essential in many fields, including physics, engineering, economics, and computer science. They provide a powerful tool for solving complex problems and modeling real-world scenarios.

Algebraic Expressions Formulas
Algebraic expressions can be simplified and manipulated using various formulas and identities. These formulas help us perform calculations, factorize expressions, and solve equations. Let’s explore some commonly used algebraic expression formulas:
- Distributive Property: The distributive property states that for any three numbers
a,b, andc, the product ofaand the sum ofbandcis equal to the sum of the products ofaandbandaandc. Mathematically, it can be represented as:a(b + c) = ab + acThe distributive property is extremely useful when expanding and simplifying algebraic expressions. - Binomial Formula: The binomial formula allows us to expand a binomial raised to a power
n. It can be stated as:(a + b)^n = C(n, 0)a^n b^0 + C(n, 1)a^(n-1) b^1 + C(n, 2)a^(n-2) b² + ... + C(n, n-1)a^1 b^(n-1) + C(n, n)a^0 b^nHere,C(n, k)represents the binomial coefficient, which can be calculated using the combination formula. - Quadratic Formula: The quadratic formula is used to find the roots or solutions of a quadratic equation of the form
ax² + bx + c = 0. It can be stated as:x = (-b ± √(b² - 4ac)) / (2a)The quadratic formula is derived using the method of completing the square and is widely used in solving quadratic equations.
These are just a few examples of algebraic expression formulas. There are many more formulas and identities that can be used to simplify, expand, and solve algebraic expressions. Understanding and applying these formulas can greatly enhance your ability to work with algebraic expressions.
How to Solve Algebraic Equations?
Solving algebraic equations involves finding the values of variables that satisfy the equation. This can be done by manipulating the equation using algebraic operations and techniques. Here’s a step-by-step guide on how to solve algebraic equations:
- Clear Parentheses: If the equation contains parentheses, start by removing them using the distributive property. Distribute the terms inside the parentheses to all terms outside the parentheses.
- Combine Like Terms: Combine like terms on both sides of the equation. Like terms have the same variables and exponents. Add or subtract the coefficients of like terms to simplify the equation.
- Isolate the Variable: Move all terms containing the variable to one side of the equation and constants to the other side. Use addition or subtraction to isolate the variable on one side.
- Simplify: Simplify both sides of the equation by performing any necessary operations such as addition, subtraction, multiplication, and division. Apply the order of operations to simplify the equation further.
- Solve for the Variable: Solve for the variable by applying inverse operations to both sides of the equation. Undo the operations that were done to isolate the variable.
- Check your Solution: Substitute the value of the variable found in step 5 back into the original equation to verify that it satisfies the equation. If the equation is true, the value is a valid solution.
By following these steps, you can systematically solve algebraic equations and find the values of variables that make the equation true. Practice is key to becoming proficient in solving algebraic equations, so don’t hesitate to tackle a variety of problems to enhance your skills.
Types of Algebraic Expressions
Algebraic expressions can be classified into various types based on their structure and properties. Let’s explore some of the major types of algebraic expressions:
Monomial Expression
A monomial expression is an algebraic expression with only one term. It consists of a single variable or constant, or a product of variables and/or constants. Monomial expressions are often used to represent linear relationships and simple mathematical concepts. Examples of monomial expressions include 3x, 2y², and -5.
Binomial Expression
A binomial expression is an algebraic expression composed of two terms connected by an operation symbol. The terms can be monomials or combinations of monomials. Binomial expressions are commonly used to represent quadratic relationships and polynomial expressions of degree two. Examples of binomial expressions include 2x + 3, x² - 4, and 3xy + 2y².
Polynomial Expression
A polynomial expression is an algebraic expression with one or more terms, each of which is a monomial or a combination of monomials. Polynomial expressions can have any number of terms greater than one and are often used to represent higher-degree relationships and complex mathematical concepts. Examples of polynomial expressions include 4x³ + 2x² - 7x + 5, x⁴ - 3x² + 2, and 3xy² + 4x²y - 2y.
Numeric Expression
A numeric expression is an algebraic expression that consists of numbers and mathematical operations but does not contain any variables. Numeric expressions involve only constants and arithmetic operations such as addition, subtraction, multiplication, and division. Examples of numeric expressions include 3 + 5, 4 * (2 - 1), and sqrt(9) - 2.
Variable Expression
A variable expression is an algebraic expression that contains variables along with numbers and mathematical operations. Variable expressions are used to represent mathematical relationships in terms of unknown quantities. Examples of variable expressions include 2x + 3y, ax² + bx + c, and sin(x) + cos(y).
Understanding the different types of algebraic expressions allows us to classify mathematical relationships and solve a wide range of problems. By analyzing the structure and properties of an expression, we can apply appropriate techniques and strategies to manipulate and simplify the expression effectively.
Methods to Verify Algebraic Identities
Algebraic identities are mathematical statements that are always true for all values of the variables involved. They are derived from algebraic expressions and provide useful properties and relationships between variables, constants, and operations. Verifying algebraic identities is an essential skill in algebra and involves confirming their validity for all possible values of the variables.
There are several methods to verify algebraic identities. Let’s explore two commonly used methods:
Substitution Method
The substitution method involves substituting specific values for the variables in an algebraic identity and checking if the equation holds true. By substituting different values and evaluating both sides of the equation, we can determine if the identity is valid.
For example, let’s verify the algebraic identity (a + b)² = a² + 2ab + b² using the substitution method. We can substitute specific values for a and b and compare the values on both sides of the equation.
Let’s choose a = 3 and b = 5:
(3 + 5)² = 3² + 2(3)(5) + 5²
8² = 9 + 30 + 25
64 = 64
Since both sides of the equation evaluate to the same value, the identity (a + b)² = a² + 2ab + b² holds true for a = 3 and b = 5. We can repeat this process for different values of a and b to verify the identity for all possible values.
Activity Method
The activity method involves using geometric or visual representations to verify algebraic identities. This method is particularly useful for verifying identities involving squares, rectangles, or other geometric shapes.
For example, let’s verify the algebraic identity (a + b)(a - b) = a² - b² using the activity method. We can represent the left side of the equation as a rectangle with side lengths a + b and a - b, and the right side as the difference of squares a² - b². By comparing the areas of the rectangle and the difference of squares, we can verify the identity geometrically.
By using the substitution and activity methods, we can confidently verify algebraic identities and establish their validity for all values of the variables. These methods provide a systematic approach to confirm the mathematical relationships expressed by the identities.
Frequently Asked Questions About Algebraic Expressions
What are Algebraic Identities for Class 8?
Algebraic identities for Class 8 refer to specific formulas and equations that are taught at the 8th-grade level. These identities are derived from algebraic expressions and are used to simplify expressions, solve equations, and perform calculations. Examples of algebraic identities for Class 8 include the distributive property, binomial formulas, and quadratic formulas.
What are Algebraic Identities for Class 7?
Algebraic identities for Class 7 are foundational concepts that introduce students to the world of algebra and help them understand the relationships between variables and expressions. These identities include the commutative property, associative property, and distributive property, among others. They provide the building blocks for more complex algebraic concepts taught in higher grades.
How to derive algebraic expressions?
To derive algebraic expressions, you need to understand the problem or situation and translate it into a mathematical representation. Identify the variables involved and determine how they are related to each other. Use appropriate mathematical operations and symbols to express these relationships. Deriving algebraic expressions requires critical thinking and problem-solving skills.
Are algebraic expressions polynomials?
Not all algebraic expressions are polynomials, but all polynomials are algebraic expressions. A polynomial is an algebraic expression with one or more terms, each consisting of a variable raised to a non-negative integer exponent, multiplied by a coefficient. Algebraic expressions can be more general, including irrational numbers, fractions, and other types of terms.
How do you evaluate algebraic expressions?
To evaluate algebraic expressions, substitute the given values for the variables in the expression and perform the necessary calculations. Substitute each variable’s value into the expression, following the order of operations (PEMDAS: Parentheses, Exponents, Multiplication and Division from left to right, and Addition and Subtraction from left to right). Simplify the expression step by step until you obtain a numerical value.
How do you write an algebraic expression?
To write an algebraic expression, use variables, constants, coefficients, and algebraic operations to represent a mathematical relationship or rule. Identify the unknown quantities and assign variables to them. Use appropriate symbols and operations to express the relationship between the variables and constants. Write the expression in a clear and concise manner, following the conventions of algebraic notation.
What are Terms in Algebraic Expressions?
Terms are the building blocks of algebraic expressions. A term can be a variable alone, a constant alone, or a combination of variables and constants multiplied or divided by each other. Terms are separated by addition or subtraction symbols. Each term can have its own coefficient and variable part. Understanding terms is crucial for simplifying and manipulating algebraic expressions.
What is an algebraic form?
An algebraic form refers to the way an equation or expression is written using variables, constants, coefficients, and algebraic operations. It represents a mathematical relationship or rule that can be applied to different values of the variables. Algebraic forms allow us to generalize mathematical concepts and solve complex problems by providing a flexible representation of mathematical relationships.
Is 5 an algebraic expression?
No, 5 is not an algebraic expression because it does not involve any variables. An algebraic expression must have at least one variable along with constants, coefficients, and algebraic operations. However, 5 can be considered a constant term in an algebraic expression.
Is 4 an algebraic expression?
No, 4 is not an algebraic expression because it does not involve any variables. An algebraic expression must have at least one variable along with constants, coefficients, and algebraic operations. However, 4 can be considered a constant term in an algebraic expression.
Understanding the basics of algebraic expressions is essential for tackling more complex mathematical concepts and problem-solving. By mastering algebraic expressions, you will gain a solid foundation in algebra and open doors to a wide range of mathematical applications. Practice and explore different examples to enhance your understanding and proficiency in working with algebraic expressions.
Solved Examples on How to Use the Algebraic Expressions
Let’s look at some solved examples to understand how to use algebraic expressions:
Example 1: Simplify the expression 3x + 2y - x + y.
Solution: Combine the like terms: (3x - x) + (2y + y) => 2x + 3y.
Example 2: Evaluate the expression 4x - 3y for x = 2 and y = 1.
Solution: Substitute 2 for x and 1 for y: 4(2) - 3(1) => 8 - 3 => 5.
How Kunduz Can Help You Learn Algebraic Expressions?
Kunduz is an innovative learning platform that offers personalized assistance to students. It uses advanced technology and a team of expert educators to provide detailed solutions to a wide range of academic questions, including those on algebraic expressions. Whether you’re struggling with understanding the concept of algebraic expressions, need help with homework problems, or want to practice ahead of a test, Kunduz can be a valuable learning companion.
