In the world of geometry, angles play a crucial role in understanding the relationships between lines and shapes. One important concept to grasp is that of alternate interior angles. These angles are formed when a transversal line intersects two or more parallel lines. By studying alternate interior angles, we can gain insight into the properties of parallel lines, solve geometric problems, and prove theorems.
What are the Alternate Interior Angles?
Alternate interior angles are a pair of angles that are formed on the inner side of the parallel lines but on the opposite sides of the transversal. In simpler terms, they are angles that lie between two lines and are on the alternate opposite sides of the transversal.
Alternate Interior Angles Theorem
The alternate interior angles theorem states that when a transversal crosses two parallel lines, the alternate interior angles formed are congruent. In other words, if the lines are parallel, then the alternate interior angles will have the same measure.
Let’s consider an example to understand the theorem better. Suppose we have two parallel lines, line p and line q, intersected by a transversal line t. We label the alternate interior angles as ∠2 and ∠7, as well as ∠3 and ∠6. The theorem states that if line p is parallel to line q, then ∠2 will be congruent to ∠7, and ∠3 will be congruent to ∠6.
The alternate interior angles theorem is a fundamental property of parallel lines and is widely used in geometry proofs and calculations.
Antithesis of The Theorem
The converse of the alternate interior angles theorem states that if two lines are intersected by a transversal, and the alternate interior angles formed are congruent, then the lines are parallel. In other words, if the alternate interior angles are equal, then the lines must be parallel.
The converse of the theorem allows us to determine whether lines are parallel based on the congruence of their alternate interior angles.
Alternate Interior Angles Theorem Proof
To prove the alternate interior angles theorem, we need to show that when two parallel lines are intersected by a transversal, the alternate interior angles formed are congruent.
Given: Lines p and q are parallel, and line t is the transversal intersecting p and q.
To Prove: ∠2 = ∠7 and ∠3 = ∠6
Proof:
- Step 1: By the definition of parallel lines, we know that if two lines are parallel, then the corresponding angles formed by the transversal and the lines are congruent. Therefore, ∠1 = ∠6 and ∠2 = ∠7.
- Step 2: By the definition of alternate interior angles, we know that ∠1 and ∠2 are alternate interior angles, as well as ∠6 and ∠7.
- Step 3: Combining Step 1 and Step 2, we can conclude that ∠1 = ∠6 and ∠2 = ∠7, which means that the alternate interior angles are congruent.
- Step 4: Similarly, by the properties of parallel lines and alternate interior angles, we can show that ∠3 = ∠6 and ∠2 = ∠7, which further proves the congruence of the alternate interior angles.
Therefore, the alternate interior angles theorem is proven.
Antithesis of The Theorem
To prove the converse of the alternate interior angles theorem, we need to show that if two lines are intersected by a transversal, and the alternate interior angles formed are congruent, then the lines are parallel.
Given: Lines p and q are intersected by a transversal line t, and ∠2 = ∠7 and ∠3 = ∠6.
To Prove: p is parallel to q.
Proof:
- Step 1: Assume that lines p and q are not parallel.
- Step 2: If lines p and q are not parallel, then the alternate interior angles formed by the transversal t should not be congruent.
- Step 3: However, we are given that ∠2 = ∠7 and ∠3 = ∠6, which contradicts our assumption in Step 1.
- Step 4: Therefore, our assumption that lines p and q are not parallel is incorrect, and we can conclude that p is parallel to q.
Hence, the converse of the alternate interior angles theorem is proven.
Properties of Alternate Interior Angles
Alternate interior angles possess several properties that are useful in geometric analysis and problem-solving:
- Congruence: Alternate interior angles formed by a transversal intersecting two parallel lines are congruent. This means that they have the same measure.
- Opposite Sides: Alternate interior angles are located on the opposite sides of the transversal line.
- Interior Angles: Alternate interior angles are located inside the parallel lines.
- Corresponding Angles: Corresponding angles are another pair of angles formed by a transversal intersecting two parallel lines. Corresponding angles are equal when the lines are parallel.
- Consecutive Interior Angles: Consecutive interior angles are a pair of interior angles that are on the same side of the transversal. Consecutive interior angles are supplementary, meaning that their measures add up to 180 degrees.
These properties of alternate interior angles help us understand the relationships between lines and angles and allow us to solve various geometric problems.
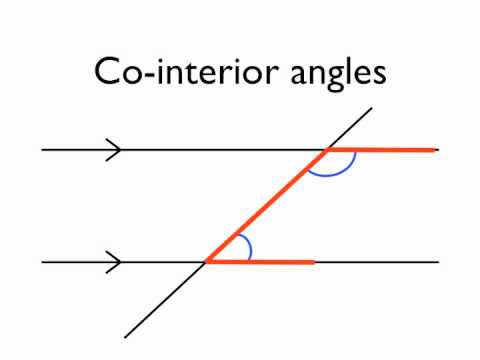
Co-interior Angles
Co-interior angles, also known as consecutive interior angles, are a pair of angles that are on the same side of the transversal line. Co-interior angles are supplementary, which means that their measures add up to 180 degrees. This is true for both parallel and non-parallel lines.
Alternate Interior Angles are Equal
The alternate interior angles theorem states that when a transversal intersects two parallel lines, the alternate interior angles are congruent. In other words, if the lines are parallel, then the alternate interior angles will have the same measure.
For example, if angles A and B are alternate interior angles, then they are congruent. This property of alternate interior angles is crucial in geometry and is utilized in many proofs and computations involving parallel lines.
Alternate Interior Angles Supplementary
While alternate interior angles are congruent for parallel lines, they are supplementary for non-parallel lines. Supplementary angles are angles that add up to 180 degrees.
In the case of non-parallel lines intersected by a transversal, the alternate interior angles are supplementary. This means that their measures add up to 180 degrees.
Alternate Interior Angles in a Triangle
In a triangle, the alternate interior angles are the angles formed between a side of the triangle and a transversal line that intersects the other two sides. These angles are not necessarily congruent unless the triangle is isosceles or equilateral.
The concept of alternate interior angles in a triangle is useful when solving for unknown angles or proving geometric properties.
How Do You Spot Alternate Interior Angles?
To spot alternate interior angles, you need to identify the transversal line that intersects two or more parallel lines. The alternate interior angles are the angles that lie on the inner side of the parallel lines but on the opposite sides of the transversal. They are located between the parallel lines and are on the alternate opposite sides of the transversal. By visually observing the angles formed, you can determine which angles are alternate interior angles.
Alternate Interior Angles Are Congruent
One of the fundamental properties of alternate interior angles is that they are congruent when formed by a transversal intersecting two parallel lines. This means that their measures are equal. If the lines are parallel, then the alternate interior angles will have the same measure.
The congruence of alternate interior angles is a crucial concept in geometry and is used to solve problems involving parallel lines and transversals.
How Kunduz Can Help You Learn Alternate Interior Angles?
At Kunduz, we understand the importance of mastering geometry concepts such as alternate interior angles. Our platform offers a comprehensive range of educational resources, including video lessons, interactive quizzes, and step-by-step explanations. With Kunduz, you can learn at your own pace, reinforce your understanding through practice, and gain the confidence to excel in geometry and mathematics.
Visit Kunduz today and start your journey towards mastering alternate interior angles and other key concepts in geometry.
