Angles are fundamental concepts in geometry that help us understand the relationships between lines and shapes. They play a crucial role in various fields, including mathematics, architecture, engineering, and physics. By understanding angles, we can analyze and design structures, solve problems involving measurements, and even appreciate the beauty of the world around us.
In this article, we will explore the definition of angles, their different types, how to measure and construct them, and their applications in real life. We will delve into concepts such as corresponding angles, interior and exterior angles, complementary and supplementary angles, and much more. So let’s dive into the fascinating world of angles!
What is an Angle?
An angle is formed when two lines or rays meet at a common endpoint, known as the vertex. The lines or rays that form the angle are called the arms of the angle. It is the measure of the “opening” between the arms, indicating the amount of rotation or turn between them. Angles are typically represented using the symbol ∠.
Angles can be classified based on their measurements. They can be acute, right, obtuse, straight, reflex, or complete angles. Each type has specific characteristics that contribute to its unique properties and applications. Understanding these types of angles is essential for solving geometry problems and analyzing various geometric shapes.
Symbol of Angle
Angles are commonly represented using the symbol ∠, which resembles a curved “L” shape. This symbol is used to denote the presence of an angle in mathematical equations, diagrams, and geometric proofs. It helps us differentiate angles from other geometric elements and indicates their significance in the given context.
Parts of an Angle
To fully understand angles, it’s important to familiarize ourselves with their different parts. An angle consists of three main components: the vertex, the arms, and the reference line.
Vertex of the Angle
The vertex is the common endpoint where the two arms of the angle meet. It is represented by a single point and serves as the starting point for measuring and analyzing the angle. The vertex is crucial in determining the position and orientation of the angle within a geometric figure.

Arms of the Angle
The arms of an angle are the two lines or rays that extend from the vertex. They form the sides of the angle and determine the “opening” or measure of the angle. The length and position of the arms play a crucial role in defining the type and properties of the angle.

Measure of an Angle
The measure of an angle determines the degree of rotation or turn between its arms. Angles are commonly measured in degrees (°) using a protractor. A full rotation around a point is equivalent to 360°, and angles can range from 0° (a zero angle) to 360° (a complete angle).
Initial Side
The initial side of an angle is the reference line or starting point from which the angle is measured. It provides a standard reference for determining the position and orientation of the angle. The initial side is an essential element when measuring and constructing angles accurately.
Terminal Side
The terminal side of an angle is the side that extends from the vertex to indicate the measure of the angle. It forms the “opening” or rotation between the arms and helps us visualize the angle’s magnitude. The terminal side is vital in understanding the concept of angles and their properties.
Understanding the parts of an angle is essential for accurately measuring, constructing, and analyzing angles in various geometric scenarios. By knowing these components, we can effectively communicate and work with angles in mathematical and real-world contexts.
Types of Angles
Angles can be classified into different types based on their measures and characteristics. Each type has distinct properties and applications in geometry. Let’s explore the various types of angles in detail.
| Type of angles | Description |
| Acute Angle | < 90° |
| Obtuse Angle | > 90° |
| Right Angle | = 90° |
| Straight Angle | =180° |
| Reflex Angle | >180° |
| Full rotation/complete angle | =360° |
Acute Angle
An acute angle is an angle that measures greater than 0° and less than 90°. It represents a small “opening” or rotation between the arms, indicating a sharp turn. In an acute angle, the arms are closer together, forming a narrow wedge-like shape.
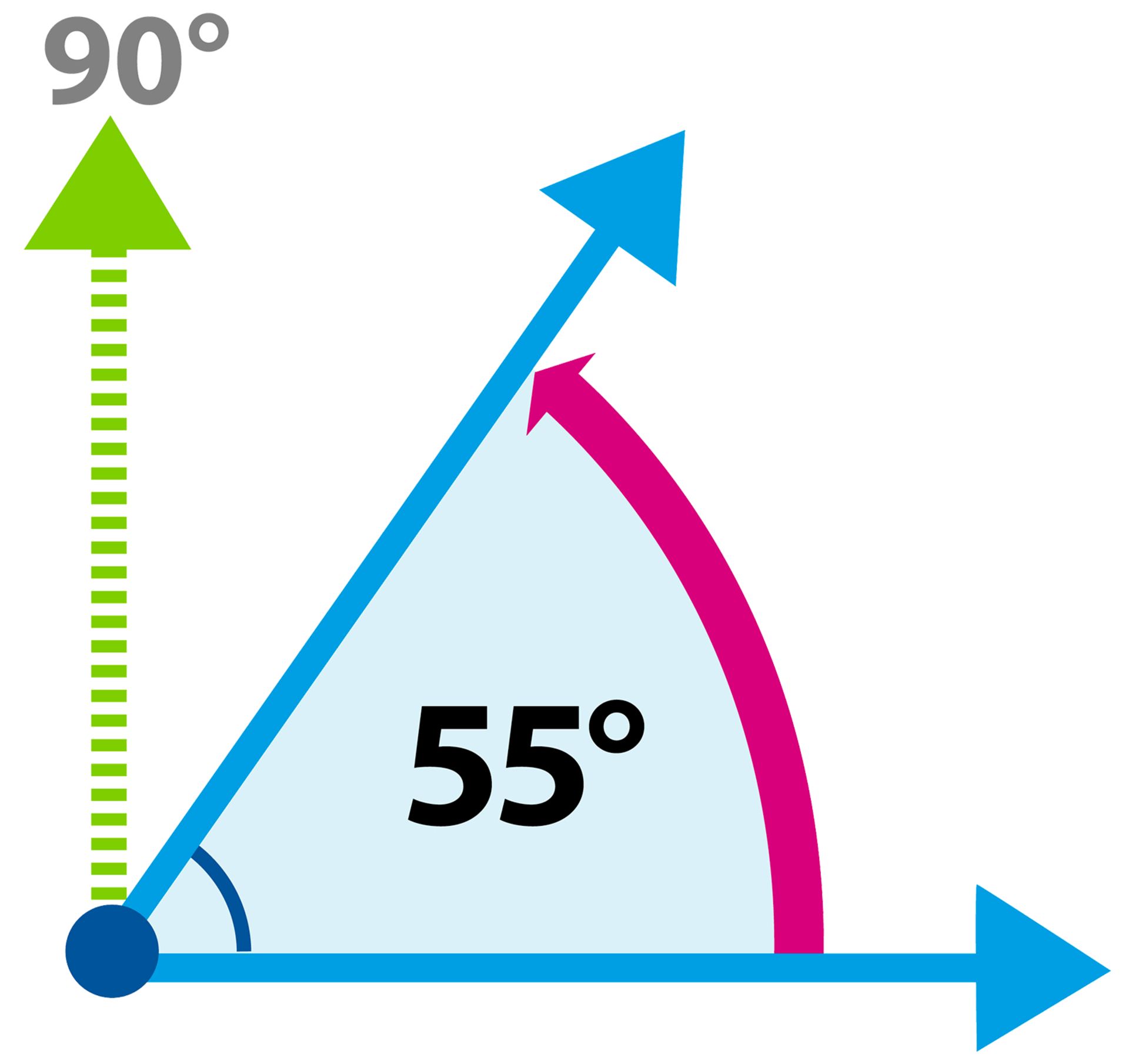
How to Measure an Acute Angle?
To measure an acute angle, we can use a protractor. Place the protractor with its center on the vertex of the angle and align one of the arms with the protractor’s baseline. Read the degree measurement where the other arm intersects the protractor’s scale. This measurement represents the size of the acute angle.
Right Angle
A right angle is an angle that measures exactly 90°. It forms a perfect “L” shape, resembling the corner of a square or rectangle. In a right angle, the arms are perpendicular to each other, creating a 90-degree turn.
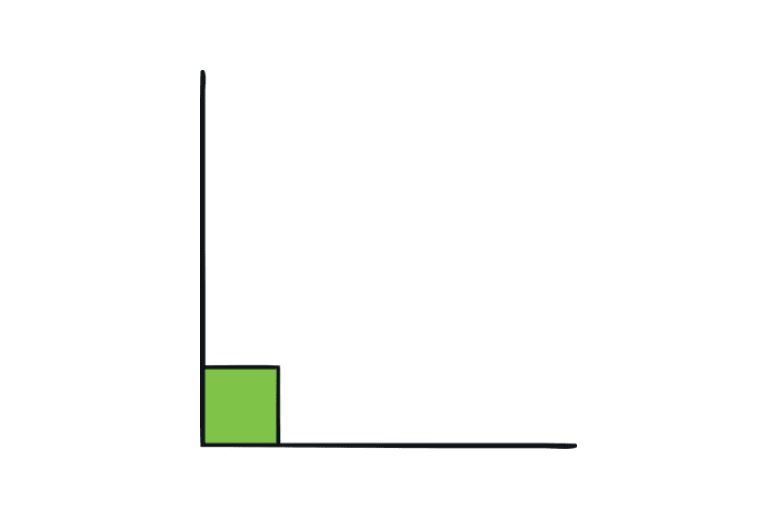
How to Measure a Right Angle?
Measuring a right angle is straightforward. Align the protractor’s baseline with one arm of the angle, ensuring that the center of the protractor is at the vertex. Read the degree measurement where the other arm intersects the protractor’s scale. The measurement should be exactly 90°, indicating a right angle.
Obtuse Angle
An obtuse angle is an angle that measures greater than 90° and less than 180°. It represents a wide “opening” or rotation between the arms, indicating a blunt turn. In an obtuse angle, the arms are further apart, forming an open wedge-like shape.
![What is Obtuse Angle? [Definition Facts & Example]](https://cdn-skill.splashmath.com/panel-uploads/GlossaryTerm/90faef6aaa3949d9b94e4ecc4e326d5d/1560256314_obtuse-angle.png)
How to Measure an Obtuse Angle?
To measure an obtuse angle, follow the same procedure as measuring an acute angle using a protractor. Align the protractor’s baseline with one arm of the angle, ensuring that the center of the protractor is at the vertex. Read the degree measurement where the other arm intersects the protractor’s scale. The measurement should be greater than 90° but less than 180°, indicating an obtuse angle.
Straight Angle
A straight angle is an angle that measures exactly 180°. It forms a straight line, resembling a perfectly extended arm. In a straight angle, the arms are collinear, creating a straight line.

How to Measure a Straight Angle?
Measuring a straight angle is similar to measuring a right angle. Align the protractor’s baseline with one arm of the angle, ensuring that the center of the protractor is at the vertex. Read the degree measurement where the other arm intersects the protractor’s scale. The measurement should be exactly 180°, indicating a straight angle.
Reflex Angle
A reflex angle is an angle that measures greater than 180° and less than 360°. It represents an “opening” or rotation between the arms that exceeds a straight angle. In a reflex angle, the arms extend beyond a straight line, creating a wide wedge-like shape.

How to Measure a Reflex Angle?
Measuring a reflex angle follows the same procedure as measuring an acute or obtuse angle using a protractor. Align the protractor’s baseline with one arm of the angle, ensuring that the center of the protractor is at the vertex. Read the degree measurement where the other arm intersects the protractor’s scale. The measurement should be greater than 180° but less than 360°, indicating a reflex angle.
Complete Angle
A complete angle is an angle that measures exactly 360°. It represents a full rotation or turn around a point. In a complete angle, the arms form a complete circle, returning to their starting position.

How to Measure a Complete Angle?
Measuring a complete angle is similar to measuring a straight angle or any other angle. Align the protractor’s baseline with one arm of the angle, ensuring that the center of the protractor is at the vertex. Read the degree measurement where the other arm intersects the protractor’s scale. The measurement should be exactly 360°, indicating a complete angle.
Understanding the different types of angles allows us to identify and analyze angles in various geometric scenarios. Each type has its unique properties and applications, contributing to a deeper understanding of geometry and its real-world implications.
Angle Based on Rotation
Angles can also be classified based on their direction of rotation. They can be positive or negative, depending on the direction in which they are measured. Let’s explore these types of angles in detail.

Positive Angles
Positive angles are angles measured in the counterclockwise or anti-clockwise direction from the baseline or initial side. They are represented by a positive measurement and are commonly used in mathematical calculations and geometric constructions. Positive angles are associated with a sense of forward motion or rotation.
Negative Angles
Negative angles are angles measured in the clockwise direction from the baseline or initial side. They are represented by a negative measurement and are the opposite of positive angles. Negative angles are less common in mathematical calculations but are still used in certain contexts, such as trigonometry and polar coordinates. Negative angles are associated with a sense of backward motion or rotation.
Understanding positive and negative angles allows us to work with angles in different mathematical contexts and analyze rotational motion in physical systems. These classifications help us interpret the direction and orientation of angles accurately.
How to Measure an Angle?
To measure angles accurately, we use a measuring tool called a protractor. A protractor is a semicircular instrument with degree markings along its curved edge. It provides a consistent and standardized way to measure angles in degrees.
Here’s a step-by-step guide on how to measure an angle using a protractor:
- Place the protractor on a flat surface, ensuring that it lies flat without any tilt or distortion.
- Position the protractor so that the center point lines up with the vertex of the angle you want to measure.
- Align the baseline of the protractor with one arm of the angle, making sure it is parallel to the arm.
- Read the degree measurement where the other arm intersects the protractor’s curved edge.
- Note the measurement and record it as the measure of the angle.
It’s important to handle the protractor carefully and align it accurately to obtain precise angle measurements. Practicing with different angles and using the protractor correctly will improve your skill in measuring angles with accuracy and confidence.
How to Construct Angles?
Constructing angles is an essential skill in geometry. It allows us to create angles with specific measurements and positions. By using a protractor, we can accurately construct angles based on their desired measurements. Here’s a step-by-step guide on how to construct angles using a protractor:
- Start by drawing a straight line to serve as the initial side or baseline of the angle. Label the endpoints of the line as points A and B.
- Place the center of the protractor on point B, aligning the baseline of the protractor with the line AB.
- Locate the degree measurement on the protractor that corresponds to the desired angle measurement. This will determine the position of the terminal side of the angle.
- Draw a line from point B to the degree measurement on the protractor, extending it beyond point B. This line forms the terminal side of the angle.
- Label the point where the terminal side intersects the baseline as point C. The angle ABC is now constructed.
By following these steps and using the protractor accurately, you can construct angles of specific measurements and explore the properties and relationships of angles in geometric figures.
Corresponding Angles
Corresponding angles are pairs of angles situated in the same relative position at the intersection of a transversal with two lines. If the two lines are parallel, then corresponding angles are congruent.
Interior and Exterior Angles
In addition to corresponding angles, it’s important to understand interior and exterior angles. These angles play a significant role in the study of polygons and provide insights into the properties of shapes with multiple sides.
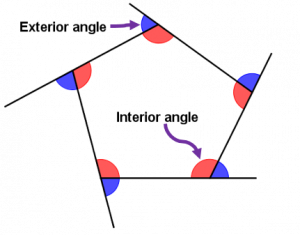
Interior Angles
Interior angles are the angles formed inside a polygon or a closed shape. In a polygon with n sides, the sum of all interior angles can be calculated using the formula (n-2) * 180°. For example, in a triangle (a polygon with 3 sides), the sum of interior angles is (3-2) * 180° = 180°.
Interior angles have several properties:
- The sum of all interior angles in a polygon is equal to (n-2) * 180°, where n is the number of sides.
- In a regular polygon (a polygon with all sides and interior angles congruent), each interior angle is equal to (n-2) * 180° / n.
Understanding interior angles helps in analyzing the properties of polygons, determining the sum of angles in a shape, and solving problems involving geometric figures.
Exterior Angles
Exterior angles are the angles formed outside a polygon or a closed shape. They are formed by extending one side of the polygon until it intersects the adjacent side. In a polygon with n sides, the sum of all exterior angles is always 360°.
Exterior angles have several properties:
- The sum of all exterior angles in a polygon is always equal to 360°.
- The measure of each exterior angle in a regular polygon is equal to 360° / n, where n is the number of sides.
Understanding exterior angles helps in analyzing the properties of polygons, determining the sum of exterior angles in a shape, and solving problems involving geometric figures.
Complementary and Supplementary Angles
Complementary and supplementary angles are two types of angle pairs that have specific relationships with each other. Understanding these relationships is essential for solving problems involving angle measurements and analyzing geometric figures.
(272).jpg)
Complementary Angles
Complementary angles are a pair of angles that add up to 90°. In other words, if the sum of two angles is 90°, they are complementary angles. Complementary angles are often seen in right triangles, where one angle is a right angle (90°).
For example:
- If angle A measures 30°, its complementary angle B would measure 60° because 30° + 60° = 90°.
- If angle C measures 45°, its complementary angle D would measure 45° because 45° + 45° = 90°.
Complementary angles have several properties:
- The sum of two complementary angles is always 90°.
- Complementary angles are often seen in right triangles, where one angle is a right angle.
- Complementary angles can be used to find the measure of one angle when the measure of the other angle is known.
Supplementary Angles
Supplementary angles are a pair of angles that add up to 180°. In other words, if the sum of two angles is 180°, they are supplementary angles. Supplementary angles are often seen in straight lines, where the sum of the angles is a straight angle.
For example:
- If angle X measures 120°, its supplementary angle Y would measure 60° because 120° + 60° = 180°.
- If angle P measures 150°, its supplementary angle Q would measure 30° because 150° + 30° = 180°.
Supplementary angles have several properties:
- The sum of two supplementary angles is always 180°.
- Supplementary angles are often seen in straight lines, where the sum of the angles is a straight angle.
- Supplementary angles can be used to find the measure of one angle when the measure of the other angle is known.
Understanding complementary and supplementary angles helps in solving problems involving angle measurements, classifying angles, and analyzing geometric figures. These angle relationships contribute to a deeper understanding of geometry and its real-world applications.
Solved Examples On Angles
To understand the concept of angles better, let’s look at some solved examples:
Example 1: Find the reflex angle of ∠x, if the value of ∠x is 75 degrees.
To find the reflex angle, we subtract the given angle from 360°. Reflex ∠x = 360° – 75° = 285°
Example 2: Solve for x.
Given, 5x – 70 = 105 (alternate interior angles) Solving for x, we get x = 35°
Example 3: In a triangle ABC, ∠A = 90 and ∠B = 30. Find ∠C.
The sum of all angles in a triangle is 180°. Hence, ∠C = 180° – (∠A + ∠B) = 60°.
Angle Measurement
Angles can be measured in different units, depending on the context and application. The two most common units for measuring angles are degrees and radians. Let’s explore each unit in detail.
Degree of an Angle
Degrees are a common unit for measuring angles. A degree is defined as 1/360th of a full rotation around a point. A full rotation is equivalent to 360 degrees. Each degree can be further divided into minutes (‘) and seconds (“). One degree is equal to 60 minutes, and one minute is equal to 60 seconds.
To measure an angle in degrees, we use a protractor or other measuring tools. The size of the angle is determined by the amount of rotation or turn between its arms. For example, a right angle measures 90 degrees, while a straight angle measures 180 degrees.
Degree measurements are widely used in various fields, including mathematics, physics, engineering, and navigation. They provide a standardized and easily interpretable way to quantify and communicate angle measurements.
Radian of an Angle
Radians are another unit for measuring angles, primarily used in advanced mathematical and scientific calculations. A radian is defined as the angle subtended by an arc of a circle that is equal in length to the radius of the circle. In other words, a radian is the ratio of the length of an arc to the radius of the circle.
A complete circle has a circumference equal to 2πr, where r is the radius of the circle. Since the circumference is equal to 360 degrees, we can equate these two measurements:
360 degrees = 2π radians
From this equation, we can derive that 1 degree is equal to π/180 radians. Therefore, to convert an angle from degrees to radians, we multiply the degree measurement by π/180.
Radian measurements are commonly used in calculus, trigonometry, and other advanced mathematical and scientific disciplines. They provide a more natural and convenient way to express angle measurements in certain contexts.
Gradian of an Angle
Gradians, also known as grads, are a less common unit for measuring angles. Gradians divide a full rotation into 400 equal parts, with each gradian representing 1/400th of a full rotation. Gradians are often used in certain engineering and surveying applications, especially in Europe.
To convert between degrees and gradians, we use the following conversion factors: 1 degree = (400/360) gradians 1 gradian = (360/400) degrees
The use of gradians is less widespread compared to degrees and radians. However, they are still used in specific fields where they provide a more convenient and precise measurement for certain applications.
Understanding the different units of angle measurement allows us to work with angles in various mathematical and scientific contexts. Whether we use degrees, radians, or gradians, these units provide a standardized and consistent way to quantify and analyze angles.
What is a Zero Angle?
A zero angle is an angle that measures exactly 0°. It represents a complete absence of rotation or turn between its arms. In a zero angle, the arms coincide, forming a straight line or a flat surface.
Zero angles have several properties:
- The measure of a zero angle is exactly 0°.
- Zero angles are often seen in figures with collinear lines or flat surfaces.
- Zero angles can be used as a reference point to measure other angles or as a starting point for rotational motion.

Understanding zero angles helps us recognize and differentiate them from other types of angles. While they may not have significant practical applications, zero angles play a vital role in establishing a reference point and understanding the concept of rotation and orientation.
In conclusion, angles are essential elements in geometry that help us understand the relationships between lines and shapes. By understanding the different types of angles, their measurements, and their applications, we can solve problems, analyze geometric figures, and explore the intricate beauty of the world around us. From complementary and supplementary angles to corresponding angles and interior and exterior angles, each concept contributes to a deeper understanding of angles and their significance in mathematics and real-life scenarios. So embrace the world of angles and unlock the secrets of geometry!
