In calculus, antiderivative rules play a crucial role in finding the antiderivatives of various functions. Antiderivatives, also known as primitive functions or indefinite integrals, are the reverse process of differentiation. They help us evaluate definite integrals and find the original function when its derivative is known. Antiderivative rules make the process of finding antiderivatives easier by providing a set of formulas for different types of functions.
What is an Antiderivative?
An antiderivative of a function f(x) is a function F(x) whose derivative is equal to f(x). In other words, if F'(x) = f(x), then F(x) is an antiderivative of f(x). The process of finding antiderivatives is called antidifferentiation. Antiderivatives are essential in calculus as they allow us to evaluate definite integrals and solve various problems involving the accumulation of quantities over a given interval.

What are Antiderivative Rules?
Antiderivative rules are a set of formulas that help us find the antiderivatives of different types of functions. These rules provide a systematic approach to finding antiderivatives and simplify the process by providing a set of formulas for common functions. Some of the most commonly used antiderivative rules include the antiderivative power rule, antiderivative chain rule, antiderivative product rule, antiderivative quotient rule, antiderivative rule for scalar multiples of functions, and antiderivative rule for the sum and difference of functions.
List of Antiderivative Rules
The following is a list of commonly used antiderivative rules:

Antiderivative Power Rule
The antiderivative power rule states that the antiderivative of x^n is (1/(n+1)) * x^(n+1), where n is any real number except -1. This rule is commonly used to find the antiderivatives of functions involving powers of x.
Antiderivative Chain Rule
The antiderivative chain rule is the reverse of the chain rule in differentiation. It allows us to find the antiderivative of a composite function. If we have an integral of the form ∫f(g(x)) * g'(x) dx, the antiderivative chain rule states that the antiderivative is ∫f(u) du, where u = g(x).
Antiderivative Product Rule
The antiderivative product rule is used to find the antiderivative of a product of two functions. It states that the antiderivative of f(x) * g(x) dx is F(x) * g(x) – ∫F'(x) * g(x) dx, where F(x) is an antiderivative of f(x) and F'(x) is its derivative.
Antiderivative Quotient Rule
The antiderivative quotient rule allows us to find the antiderivative of a quotient of two functions. It states that the antiderivative of f(x) / g(x) dx is (F(x) * g(x) – ∫F'(x) * g(x) dx) / (g(x))^2, where F(x) is an antiderivative of f(x) and F'(x) is its derivative.
Antiderivative Rule for Scalar Multiple of Function
The antiderivative rule for a scalar multiple of a function states that the antiderivative of k * f(x) dx is k * F(x), where F(x) is an antiderivative of f(x) and k is a constant.
Antiderivative Rule for Sum and Difference of Functions
The antiderivative rule for the sum and difference of functions states that the antiderivative of f(x) + g(x) dx is F(x) + G(x), where F(x) is an antiderivative of f(x) and G(x) is an antiderivative of g(x).
Antiderivative Rules for Specific Functions
Different types of functions have specific antiderivative rules. Here are some of the most commonly used antiderivative rules for specific functions:
Antiderivative Rules for Trigonometric Functions
Trigonometric functions have their own set of antiderivative rules. The antiderivative rules for the six main trigonometric functions are as follows:
- The antiderivative of sin(x) is -cos(x) + C.
- The antiderivative of cos(x) is sin(x) + C.
- The antiderivative of tan(x) is -ln|cos(x)| + C.
- The antiderivative of cot(x) is ln|sin(x)| + C.
- The antiderivative of sec(x) is ln|sec(x) + tan(x)| + C.
- The antiderivative of csc(x) is ln|csc(x) – cot(x)| + C.
Antiderivative Rules for Inverse Trigonometric Functions
Inverse trigonometric functions also have their own set of antiderivative rules. The antiderivative rules for the six main inverse trigonometric functions are as follows:
- The antiderivative of arcsin(x) is x * arcsin(x) + √(1 – x^2) + C.
- The antiderivative of arccos(x) is x * arccos(x) – √(1 – x^2) + C.
- The antiderivative of arctan(x) is x * arctan(x) – (1/2) * ln(1 + x^2) + C.
- The antiderivative of arccot(x) is x * arccot(x) + (1/2) * ln(1 + x^2) + C.
- The antiderivative of arcsec(x) is x * arcsec(x) – ln|x + √(x^2 – 1)| + C.
- The antiderivative of arccsc(x) is x * arccsc(x) + ln|x + √(x^2 – 1)| + C.
Antiderivative Rules for Exponential Functions
Exponential functions have their own antiderivative rules. The antiderivative rules for the exponential function e^x and the general exponential function a^x (where a is a constant) are as follows:
- The antiderivative of e^x is e^x + C.
- The antiderivative of a^x is (a^x) / ln(a) + C.
Antiderivative Rules for Logarithmic Functions
Logarithmic functions also have specific antiderivative rules. The antiderivative rules for the natural logarithm ln(x) and the general logarithm log_a(x) (where a is a constant) are as follows:
- The antiderivative of ln(x) is x * ln(x) – x + C.
- The antiderivative of log_a(x) is x * log_a(x) – x * ln(a) + C.
Antiderivative Rules for Hyperbolic Functions
Hyperbolic functions, which are analogs of trigonometric functions, also have their own antiderivative rules. The antiderivative rules for the six main hyperbolic functions are as follows:
- The antiderivative of sinh(x) is cosh(x) + C.
- The antiderivative of cosh(x) is sinh(x) + C.
- The antiderivative of tanh(x) is ln(cosh(x)) + C.
- The antiderivative of coth(x) is ln(sinh(x)) + C.
- The antiderivative of sech(x) is arctan(sinh(x)) + C.
- The antiderivative of csch(x) is ln(tanh(x/2)) + C.
How to Find an Antiderivative?
To find an antiderivative, we can use the antiderivative rules mentioned above. The process involves identifying the type of function we are dealing with and applying the corresponding antiderivative rule. It is important to note that antiderivatives are not unique, and there can be multiple antiderivatives for a given function.
To find an antiderivative, follow these steps:
- Identify the type of function you are dealing with (algebraic, trigonometric, exponential, logarithmic, etc.).
- Use the corresponding antiderivative rule for that type of function to find the antiderivative.
- Add a constant of integration (C) to account for all possible antiderivatives of the function.
- Simplify the expression if necessary.
It is important to note that finding an antiderivative can sometimes be challenging, especially for more complex functions. In such cases, additional techniques like substitution or integration by parts may be required.
Derivatives and Antiderivatives
Derivatives and antiderivatives are closely related concepts in calculus. The derivative of a function measures its rate of change at any given point, while the antiderivative of a function represents the accumulation of quantities over a given interval.
The relationship between derivatives and antiderivatives is captured by the fundamental theorem of calculus. This theorem states that if F(x) is an antiderivative of f(x), then the definite integral of f(x) from a to b is equal to F(b) – F(a).
In other words, the process of finding an antiderivative allows us to evaluate definite integrals. This connection between derivatives and antiderivatives is a fundamental concept in calculus and is used extensively in various applications.
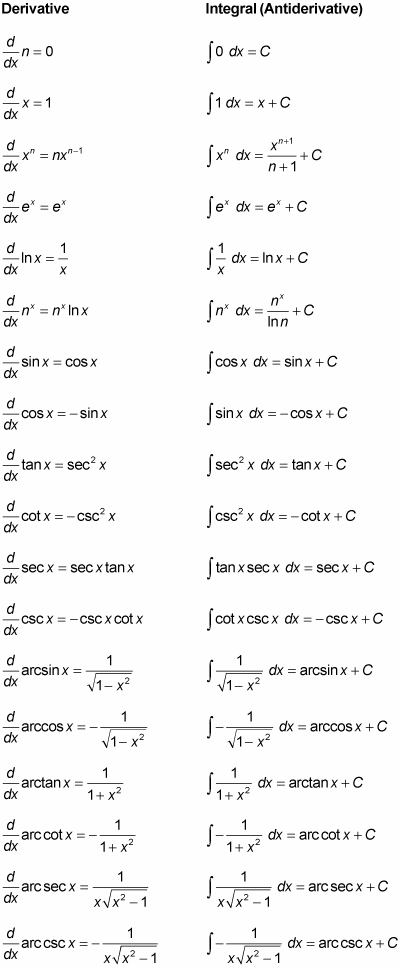
Fundamental Theorem of Calculus
The fundamental theorem of calculus is a fundamental result in calculus that establishes a connection between derivatives and antiderivatives. The theorem consists of two parts:
- The first part states that if f(x) is a continuous function on the interval [a, b], and F(x) is any antiderivative of f(x) on [a, b], then the definite integral of f(x) from a to b is equal to F(b) – F(a). Mathematically, this can be written as ∫[a, b] f(x) dx = F(b) – F(a).
- The second part of the fundamental theorem of calculus provides a method for finding antiderivatives. It states that if f(x) is a continuous function on an interval [a, b], and F(x) is any antiderivative of f(x) on [a, b], then the derivative of the definite integral of f(x) from a to x is equal to f(x). Mathematically, this can be written as d/dx ∫[a, x] f(t) dt = f(x).
The fundamental theorem of calculus is a powerful tool in calculus that allows us to evaluate definite integrals and find antiderivatives.
Solved Examples on Antiderivative Rules
Let’s look at some examples to illustrate how antiderivative rules are used to find antiderivatives:
Example 1: Find the antiderivative of the function f(x) = 3x^2 – 5x + 2.
Solution: To find the antiderivative, we can apply the antiderivative power rule. Using the power rule, we integrate each term separately:
∫ (3x^2 – 5x + 2) dx = x^3 – (5/2)x^2 + 2x + C,
where C is the constant of integration.
Example 2: Find the antiderivative of the function f(x) = sin(x) + e^x.
Solution: To find the antiderivative, we can apply the antiderivative rules for trigonometric and exponential functions:
∫ (sin(x) + e^x) dx = -cos(x) + e^x + C,
where C is the constant of integration.
Example 3: Find the antiderivative of the function f(x) = (3/x) + ln(x).
Solution: To find the antiderivative, we can apply the antiderivative rules for a quotient and logarithmic function:
∫ [(3/x) + ln(x)] dx = 3ln|x| + x ln(x) + C,
where C is the constant of integration.
These examples demonstrate how antiderivative rules can be used to find the antiderivatives of various functions.
How Kunduz Can Help You Learn Antiderivative Rules?
Kunduz is a comprehensive online learning platform that offers a wide range of resources to help you learn and understand antiderivative rules. Whether you are a student studying calculus or someone looking to refresh your knowledge, Kunduz provides a variety of tools and materials to support your learning journey.
Here’s how Kunduz can help you learn antiderivative rules:
- Interactive Lessons: Kunduz offers interactive lessons that break down complex concepts into manageable chunks. These lessons provide step-by-step explanations and examples to help you understand antiderivative rules.
- Practice Problems: Kunduz offers a wide range of practice problems to help you reinforce your understanding of antiderivative rules. These problems cover various types of functions and allow you to apply the antiderivative rules in different contexts.
- Video Tutorials: Kunduz provides video tutorials that explain antiderivative rules in a visual and engaging way. These tutorials walk you through the concepts and demonstrate how to apply the rules to solve problems.
- Personalized Learning: Kunduz offers personalized learning paths that adapt to your individual needs and pace. The platform tracks your progress and provides targeted recommendations to help you focus on areas that need improvement.
- Expert Support: Kunduz provides access to a community of expert instructors who are available to answer your questions and provide guidance. You can interact with instructors through forums, live chat, and virtual classrooms.
With Kunduz, you can learn antiderivative rules at your own pace, track your progress, and gain the confidence to tackle complex calculus problems.
Related Topics:
