Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. In trigonometry, the sine function (sin) is widely used to determine the ratio between the length of the side opposite an angle and the length of the hypotenuse in a right-angled triangle. The arcsine function (arcsin), also known as the inverse sine function, is the opposite of the sine function. It helps us find the angle corresponding to a given ratio of the side opposite to the hypotenuse. This article will explore the concept of arcsin, its formula, graph, domain and range, as well as provide examples to help you understand its applications better.
What is Arcsin?
Arcsin, denoted as arcsin(x) or sin^-1(x), is the inverse trigonometric function of the sine function. It gives us the angle (in radians or degrees) whose sine is equal to a given value x. In other words, if sin(y) = x, then arcsin(x) = y. It is important to note that arcsin(x) is not the same as 1/sin(x). Arcsin is one of the six main inverse trigonometric functions, which include arccos, arctan, arcsec, arccsc, and arccot.
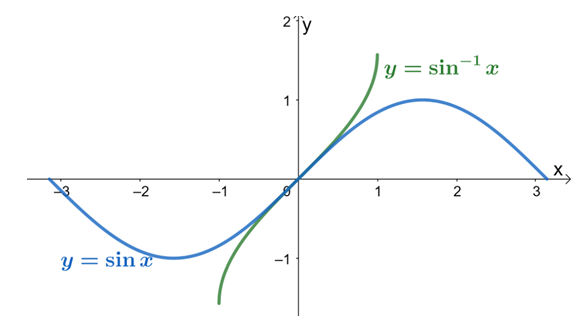
What is Sine?
Before delving into arcsin, it’s important to understand the sine function. In a right-angled triangle, the sine of an angle (θ) is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. Mathematically, it can be expressed as sin(θ) = opposite/hypotenuse. The sine function is periodic, meaning it repeats its values after a certain interval.
Inverse of Sine
The inverse of a function “undoes” the function’s operation. In the case of the sine function, the arcsin function undoes the sine function, allowing us to find the angle corresponding to a given ratio. The arcsin function takes a value x and returns the angle (in radians or degrees) whose sine is equal to x. It is important to note that the domain of arcsin is restricted to -1 ≤ x ≤ 1, as sine values are only within this range.
Arcsin(x) Formula
The formula for arcsin(x) can be derived from the definition of the sine function. In a right-angled triangle, if the ratio of the length of the side opposite to an angle (θ) to the length of the hypotenuse is x, then arcsin(x) gives us the measure of the angle θ. Mathematically, the formula for arcsin(x) is:
θ = arcsin(x)
Arcsin Graph
To visualize the arcsin function, we can plot its graph. The graph of arcsin(x) represents the values of the arcsin function for different values of x. The x-axis represents the input values (x), while the y-axis represents the corresponding angles (θ). The graph of arcsin(x) is a curve that starts at (-1, -π/2) and ends at (1, π/2). It is symmetric about the y-axis, meaning that arcsin(-x) = -arcsin(x). The range of arcsin(x) is [-π/2, π/2].
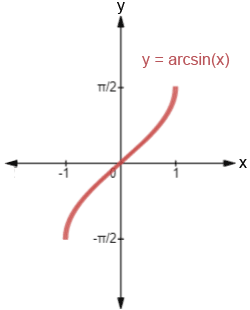
Domain and Range of Arcsin
The domain of arcsin(x) is the set of all possible input values (x) for the arcsin function. Since the sine function is defined for all real numbers, the domain of arcsin(x) is also all real numbers. However, the range of arcsin(x) is restricted to the interval [-π/2, π/2]. This means that the output (θ) of the arcsin function will always be an angle between -π/2 and π/2 (in radians) or -90° and 90° (in degrees).
Arcsin Identities
Like other trigonometric functions, arcsin has its own set of identities that can be used to simplify expressions involving arcsin. Some important arcsin identities include:
- sin(arcsin(x)) = x, if -1 ≤ x ≤ 1
- arcsin(sin(x)) = x + 2kπ, where k is an integer
- arcsin(-x) = -arcsin(x)
- arcsin(x) + arccos(x) = π/2
- arcsin(2x) = 2arcsin(x√(1 – x^2)), if -1/√2 ≤ x ≤ 1/√2
These identities can be useful in simplifying trigonometric equations and solving problems involving arcsin.
Derivative of Arcsin
The derivative of a function measures its rate of change at any given point. The derivative of arcsin(x), denoted as d/dx(arcsin(x)) or arcsin'(x), represents the rate of change of the arcsin function with respect to x. The derivative of arcsin(x) is given by:
d/dx(arcsin(x)) = 1/√(1 – x^2)
This derivative formula can be derived using the chain rule of differentiation and the fundamental trigonometric identity sin^2(x) + cos^2(x) = 1.
Integral of Arcsin
The integral of a function represents the area under the curve of that function. The integral of arcsin(x), denoted as ∫arcsin(x) dx, represents the antiderivative of the arcsin function. The integral of arcsin(x) can be calculated using integration techniques such as substitution or integration by parts. The general form of the integral of arcsin(x) is given by:
∫arcsin(x) dx = x*arcsin(x) + √(1 – x^2) + C
where C is the constant of integration.
How do you find the inverse of sine?
To find the inverse of the sine function, you can use the arcsin function. The arcsin function takes a value x and returns the angle (in radians or degrees) whose sine is equal to x. To find the inverse of sine, simply input the value of x into the arcsin function, and the angle will be returned.
What are Inverse Trigonometric Functions?
Inverse trigonometric functions are functions that “undo” the trigonometric functions. They help us find the angle corresponding to a given ratio of sides in a right-angled triangle. The six main inverse trigonometric functions are arcsin, arccos, arctan, arcsec, arccsc, and arccot. Each of these functions corresponds to a specific trigonometric ratio.
Arcsin Table
The arcsin table lists the values of arcsin(x) for different values of x. It provides a quick reference for finding the angle corresponding to a given ratio. Here is a table of some commonly used values of arcsin:
| x | arcsin(x) (in radians) | arcsin(x) (in degrees) |
|---|---|---|
| -1 | -π/2 | -90° |
| -√2/2 | -π/4 | -45° |
| 0 | 0 | 0° |
| √2/2 | π/4 | 45° |
| 1 | π/2 | 90° |
This table can be helpful in quickly determining the angle corresponding to a given sine value.
Difference Between Arcsin vs. Arccos vs. Arctan
Arcsin, arccos, and arctan are three of the six main inverse trigonometric functions. While arcsin is the inverse of the sine function, arccos is the inverse of the cosine function, and arctan is the inverse of the tangent function. Each of these functions helps us find the angle corresponding to a given ratio of sides in a right-angled triangle. The domains and ranges of these functions differ, but they all play important roles in solving trigonometric equations and problems.
Inverse Trigonometric Functions
Inverse trigonometric functions are essential tools in trigonometry. They provide a way to find the angle corresponding to a given trigonometric ratio. In addition to arcsin, arccos, and arctan, there are three more inverse trigonometric functions: arcsec, arccsc, and arccot. These functions have their own formulas, graphs, and identities, which are useful in various mathematical applications.
Solved Examples on Arcsin
Let’s solve some examples to understand how to use the arcsin function in different scenarios.
Example 1: Find the angle θ for which sin(θ) = 1/2.
Solution: Using the arcsin function, we have: θ = arcsin(1/2) θ = π/6 rad = 30°
Example 2: Find the angle θ for which sin(θ) = -√3/2.
Solution: Using the arcsin function, we have: θ = arcsin(-√3/2) θ = -π/3 rad = -60°
Example 3: Find the angle θ for which sin(θ) = 0.
Solution: Using the arcsin function, we have: θ = arcsin(0) θ = 0 rad = 0°
These examples demonstrate how the arcsin function can be used to find the angle corresponding to a given sine value.
How Kunduz Can Help You Learn Arcsin?
At Kunduz, we understand the challenges students face when learning trigonometry and its functions. That’s why we offer a wide range of resources, including interactive lessons, practice problems, and step-by-step solutions, to help you master concepts like arcsin. Our experienced tutors are here to guide you through the learning process and provide personalized support. Whether you need help with understanding the formula, graphing arcsin, or solving examples, Kunduz is here to make your learning journey enjoyable and successful. Visit our website today to explore our comprehensive trigonometry resources and start your path to success in mathematics.
