In the field of geometry, the area of a rectangle is a fundamental concept that is widely used in various real-world applications. The area of a shape refers to the amount of space enclosed by that shape. Specifically, the area of a rectangle is the region enclosed within its four sides. It can be visualized as the surface covered by the rectangle in a two-dimensional plane.
What is a Rectangle?
A rectangle is a quadrilateral with four sides and four right angles. It is a type of parallelogram where the opposite sides are equal in length and parallel to each other. Unlike a square, a rectangle does not have all sides equal in length. However, all angles of a rectangle are right angles, which means they measure 90 degrees.

What is the Area of a Rectangle?
The area of a rectangle is calculated by multiplying its length and width. The formula for the area of a rectangle can be expressed as:
Area = length x width
The units of measurement for the area of a rectangle are square units, such as square meters (m²), square centimeters (cm²), or square inches (in²). The area represents the total amount of space enclosed by the rectangle’s boundary.
Area of Rectangle Formulas
There are different formulas to calculate the area of a rectangle, depending on the given information. Here are some common formulas:
Area of Rectangle Using Diagonal
If the diagonal and one side length of a rectangle are given, the area can be calculated using the following formula:
Area = (Diagonal² – Side²) x Side
Area of Rectangle using Perimeter
If the perimeter and one side length of a rectangle are known, the area can be found using the following formula:
Area = (Perimeter ÷ 2 – Side) x Side
Area of a Rectangle When One Side is Given
If only one side length of a rectangle is given, the area can be calculated by dividing the area of a square with the same side length by 2:
Area = (Side²) ÷ 2
Area of Rectangles with Fractions
In some cases, the side lengths of a rectangle may involve fractions. To find the area in such cases, multiply the side lengths directly:
Area = Length x Width
Area of Rectangles: Square Units
The area of a rectangle is always expressed in square units. These units depend on the chosen measurement system, such as square meters (m²), square centimeters (cm²), or square inches (in²). The square units represent the number of unit squares that can fit inside the rectangle.
How to Find the Area of a Rectangle?
To find the area of a rectangle, follow these steps:
Step 1: Note the dimensions of the rectangle: Take note of the length and width (or breadth) of the given rectangle.
Step 2: Multiply the length and width values: Multiply the length and width values together to find the product.
Step 3: Write the answer in square units: The final result represents the area of the rectangle and should be expressed in square units based on the chosen measurement system.
Unit of Area of Rectangle
The unit of measurement for the area of a rectangle is always in square units. The specific square units used depend on the chosen measurement system. For example, the area can be expressed in square meters (m²), square centimeters (cm²), or square inches (in²). The square unit represents the number of unit squares that can fit inside the rectangle.
Derivation of Surface Area of Rectangle
The derivation of the formula for the area of a rectangle can be understood by dividing the rectangle into two congruent right-angled triangles. Let’s consider a rectangle ABCD, where AC is the diagonal. Divide the rectangle using the diagonal into two right-angled triangles, ABC and ADC.
The area of each right-angled triangle can be calculated using the formula for the area of a triangle, which is 1/2 times the base times the height. In this case, the base of the triangle is the length of the rectangle, and the height is the width of the rectangle.
Since the two triangles are congruent, their areas are equal. Therefore, the area of the rectangle is equal to twice the area of one of the triangles. Mathematically, we can express this as:
Area of Rectangle = 2 x Area of Triangle = 2 x (1/2 x Base x Height) = 2 x (1/2 x Length x Width) = Length x Width
Hence, the area of a rectangle is equal to the product of its length and width.
Properties of Rectangle
A rectangle has several properties that make it distinct from other shapes:
- A rectangle is a quadrilateral with four sides.
- All angles of a rectangle are right angles (measuring 90 degrees).
- The opposite sides of a rectangle are equal in length and parallel to each other.
- The diagonals of a rectangle are congruent, bisect each other, and divide the rectangle into four congruent right-angled triangles.
- A rectangle is a type of parallelogram, as it has two pairs of parallel sides.
- A square is a special case of a rectangle, where all sides are equal in length.
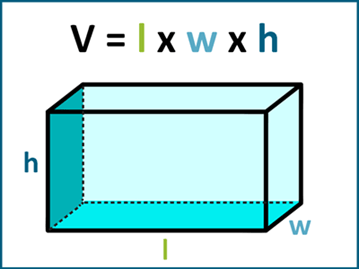
Volume of Rectangle
It is important to note that the term “area” is used to measure two-dimensional space, while the term “volume” is used to measure three-dimensional space. Therefore, the concept of volume is not applicable to rectangles, as a rectangle is a two-dimensional shape.
The volume is relevant when dealing with three-dimensional shapes such as cubes, prisms, or cylinders. For example, the volume of a rectangular prism can be calculated by multiplying the length, width, and height.
Solved Examples on Area of Rectangle
Example 1: Find the area of a rectangle whose length is 10 cm and width is 6 cm.
Solution: Given length = 10 cm and width = 6 cm. The formula to find the area of a rectangle is A = length x width. Substituting the given values, we get: Area = 10 cm x 6 cm = 60 cm² Therefore, the area of the rectangle is 60 cm².
Example 2: A rectangular garden has a length of 20 meters and an area of 150 square meters. What is the width of the garden?
Solution: Given length = 20 meters and area = 150 square meters. We can rearrange the formula for the area of a rectangle to solve for width: Area = length x width 150 square meters = 20 meters x width Dividing both sides by 20, we get: Width = 150 square meters ÷ 20 meters = 7.5 meters Therefore, the width of the garden is 7.5 meters.
Example 3: The perimeter of a rectangle is 40 feet, and its length is 12 feet. What is the width of the rectangle?
Solution: Given perimeter = 40 feet and length = 12 feet. The formula for the perimeter of a rectangle is P = 2(length + width). Substituting the given values, we get: 40 feet = 2(12 feet + width) Dividing both sides by 2, we get: 20 feet = 12 feet + width Subtracting 12 feet from both sides, we get: Width = 20 feet – 12 feet = 8 feet Therefore, the width of the rectangle is 8 feet.
How Kunduz Can Help You Learn How To Find The Area of Rectangle?
At Kunduz, we understand that learning geometry and mathematics can be challenging. That’s why we offer a wide range of resources and learning materials to help students grasp the concept of finding the area of a rectangle.
Our experienced and dedicated teachers are available to provide step-by-step guidance and explanations, making geometry and mathematics enjoyable and accessible. With our interactive online classes, students can ask questions, solve problems, and gain a deeper understanding of the area of a rectangle.
We provide comprehensive study materials, practice exercises, and solved examples to reinforce the concepts learned in class. Our goal is to empower students to excel in geometry and mathematics, building a strong foundation for their academic success.
Join Kunduz today and let us help you master the area of a rectangle and other mathematical concepts. Together, we can make learning fun and rewarding!
