In geometry, a sphere is a three-dimensional object that is perfectly round and symmetrical. It is defined as a set of points in space that are equidistant from a central point. The surface of a sphere is smooth and curved, with every point on the surface being the same distance from the center. The area occupied by the surface of a sphere is known as the surface area of a sphere.
What is Sphere?
A sphere is a three-dimensional shape that is perfectly round and symmetrical. It is similar to a circle in two dimensions, but extended into the third dimension. A sphere has no edges or vertices and is defined by its radius, which is the distance from the center of the sphere to any point on its surface. The surface of a sphere is smooth and curved, and all points on the surface are equidistant from the center.

What is the Area of Sphere?
The area of a sphere, or more specifically, the surface area of a sphere, is the region enveloped by the outer, curved surface of the sphere. The area of a sphere is expressed in square units, emphasizing its two-dimensional measurement despite the sphere being a three-dimensional object. It is calculated using a specific formula, which we will explore in the next section.
Area of Sphere Formulas
Curved Surface Area of Sphere (CSA)
The curved surface area of a sphere is the same as the total surface area of the sphere, as there are no flat surfaces on a sphere. This is calculated using the formula:
CSA of Sphere = 4πr²
Where r is the radius of the sphere.
Lateral Surface Area of Sphere (LSA)
The lateral surface area of a sphere is identical to the curved surface area since a sphere lacks flat surfaces. Thus, the formula is:
LSA of Sphere = 4πr²
Total Surface Area of Sphere (TSA)
Similarly, the total surface area of a sphere is equal to the curved surface area. Thus, the formula is:
TSA of Sphere = 4πr²
How to find the Area of a Sphere?
Calculating the area of a sphere is a straightforward process once the radius of the sphere is known. The following steps guide you through the process:
Step 1: Obtain the radius of the sphere. If the diameter is given, remember to divide it by 2 to get the radius.
Step 2: Apply the formula for the surface area of a sphere, 4πr². Substitute the value of the radius from Step 1 into the formula.
Step 3: Solve the expression to get the surface area of the sphere.
Area of Hemisphere
A hemisphere is a three-dimensional shape that is exactly half of a sphere. The total surface area of a hemisphere is the sum of half of the sphere’s surface area and the base area (which is circular). Thus, the formula for the surface area of a hemisphere is:
TSA of Hemisphere = 3πr²
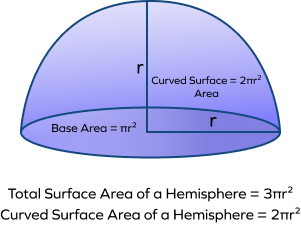
Curved Surface Area of Sphere
As already mentioned, the curved surface area of a sphere is the same as the total surface area of the sphere. This is because a sphere only has one surface, which is curved. The formula for the curved surface area of a sphere is:
CSA of Sphere = 4πr²
Archimedes Hot-Box Theorem
Archimedes, a Greek mathematician, discovered a theorem known as the “Hot-Box Theorem” that relates the surface area of a sphere to the surface area of a cylinder. According to this theorem, if a sphere and a cylinder have the same radius and height, the surface area of the sphere is equal to the lateral surface area of the cylinder. This theorem provides an alternative method to calculate the surface area of a sphere.

Derivation of Surface Area of Sphere
The surface area of a sphere can be derived by considering it as a collection of circular strips of varying radii. The surface area of each circular strip is calculated, and then the sum of all these areas is taken to find the surface area of the entire sphere. The derivation involves integrating the areas of these circular strips over the entire sphere.
Properties of Sphere
A sphere has several properties that make it unique among other three-dimensional shapes. Some of these properties include:
- A sphere has no faces or edges.
- It is perfectly symmetrical in every way.
- All points on the surface of a sphere are equidistant from the center.
- It has only one surface, which is completely curved.
- A sphere is not a polyhedron.
Volume of Sphere
The volume of a sphere is another important aspect to consider. The volume represents the amount of space that a sphere occupies in a three-dimensional space. The formula for the volume of a sphere is 4/3 πr³.
Solved Examples on Area of Sphere
Now that we have explored the concepts and formulas related to a sphere, let’s solve some examples to understand their application.
Example 1: Find the surface area of a sphere with a radius of 7 cm.
Solution: The radius of the sphere is given as 7 cm. Substituting this value into the formula for the surface area of a sphere, we get:
Surface Area = 4πr² = 4 × π × 7² = 615.75 cm²
Example 2: A sphere has a diameter of 10 cm. What is the surface area of this sphere?
Solution: The diameter of the sphere is given as 10 cm. Hence, the radius of the sphere is d/2 = 10/2 = 5 cm. Substituting this value into the formula for the surface area of a sphere, we get:
Surface Area = 4πr² = 4 × π × 5² = 314.16 cm²
Example 3: If the surface area of a sphere is 314 cm², what is its radius?
Solution: The surface area of the sphere is given as 314 cm². Using the formula for the surface area of a sphere, we can solve for the radius as follows:
Surface Area = 4πr² => 314 = 4 × π × r²
Solving for r, we get r = √(314 ÷ 4π) = 5 cm.
How Kunduz Can Help You Learn How To Find The Area of Sphere?
At Kunduz, we understand the importance of mastering mathematical concepts such as finding the area of a sphere. Our expert tutors provide personalized online math tutoring to help you understand and excel in geometry and other mathematical topics. With our interactive lessons and step-by-step guidance, you can easily grasp the concepts and develop strong problem-solving skills. Join Kunduz today and unlock your potential in mathematics!

