A parallelogram, a quadrilateral with opposite sides that are both equal and parallel, is a common shape in geometry. If you’re curious about how to find the area of a parallelogram and understand its properties, then you’re in the right place! This comprehensive guide will make you an expert in no time.
An Introduction to Area of Parallelogram
The area of a parallelogram refers to the amount of two-dimensional space it occupies. This is typically measured in square units (such as square inches, square feet, square meters, etc.). The calculation of the area is fundamental in different fields, including architecture, design, and mathematics. Understanding how to find the area of a parallelogram is a crucial aspect of geometry and can be applied to various real-world scenarios.
What is a Parallelogram?
A parallelogram is a four-sided shape, otherwise known as a quadrilateral, where the opposite sides are equal in length and parallel to one another. This includes shapes such as rectangles, squares, and rhombuses, all of which fall under the category of parallelograms.

What is the Area of a Parallelogram?
The area of a parallelogram refers to the total space enclosed within its boundaries on a flat surface. It’s measured in square units, such as square centimeters (cm²), square meters (m²), or square inches (in²), depending on the unit of measurement used for the sides.
Area of Parallelogram Formulas
Several formulas can be used to calculate the area of a parallelogram, depending on the information available. Here are some commonly used ones:
Area of Parallelogram Using Sides
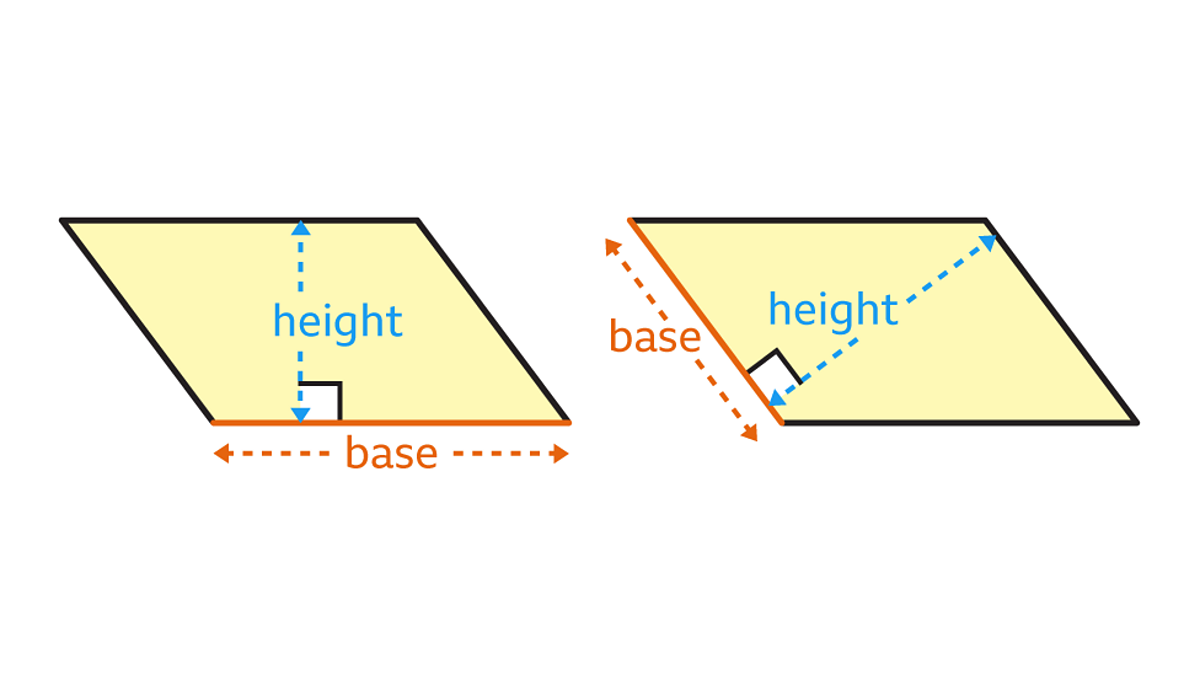
When you know the base (b) and the height (h) of the parallelogram, you can easily find its area (A) using the formula:
A = b × h
The base refers to the length of any side of the parallelogram, while the height is the perpendicular distance from the base to the opposite side.
Area of Parallelogram Without Height
If the height of the parallelogram is unknown but the lengths of the adjacent sides (a and b) and the angle (θ) between them are known, the area can be calculated using trigonometry:
A = a × b × sin(θ)
Area of Parallelogram Using Diagonals
If you know the lengths of the diagonals (d1 and d2) and the angle (y) between them, you can calculate the area using the formula:
A = ½ × d1 × d2 × sin(y)
Area of Parallelogram in Vector Form
If the sides or diagonals of the parallelogram are given in vector form, the area can be calculated using the cross product of the vectors. If a and b are vectors representing the sides, and d1 and d2 the diagonals, then the area can be found using:
A = |a × b| (for sides)
A = ½ |(d1 × d2)| (for diagonals)
Area of Parallelogram by Counting Squares
This method involves counting the number of squares inside the parallelogram on a grid paper. Each full square counts as one, while half or more than half squares can be approximated to one.
How to Find the Area of a Parallelogram?
Here’s a step-by-step guide on how to find the area of a parallelogram:
Step 1: Identify the base and the height of the parallelogram as given in the problem.
Step 2: Ensure that the base and the height are perpendicular to each other.
Step 3: Multiply the base (b) by the height (h) to get the area (A).
Step 4: The result, A, is the area of the parallelogram in square units.
Types of Parallelograms
There are three primary types of parallelograms:
- Rectangle: A parallelogram with four right angles.
- Square: A parallelogram with four equal sides and four right angles.
- Rhombus: A parallelogram with four equal sides but without right angles.
Each of these has unique properties and different formulas for finding their areas, but they all fall under the category of parallelograms.
Derivation of Surface Area of Parallelogram
The formula for the area of a parallelogram can be derived from the formula for the area of a rectangle. If we cut off a right triangle from one side of the parallelogram and attach it to the other side, we get a rectangle. This transformation doesn’t change the area, so the area of the parallelogram is equal to the area of the resulting rectangle, which is base times height.
Properties of Parallelogram
Here are some key properties of a parallelogram:
- Opposite sides are equal in length and parallel to each other.
- Opposite angles are equal in measure.
- The diagonals bisect each other.
- Each diagonal divides the parallelogram into two congruent triangles.
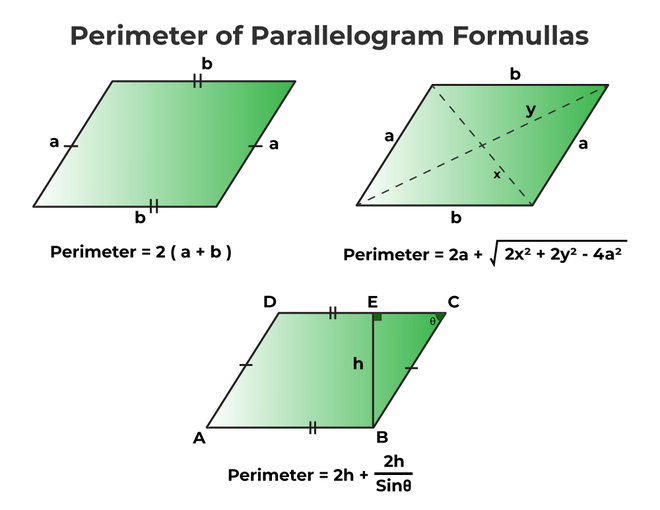
Perimeter of Parallelogram
The perimeter of a parallelogram is the sum of the lengths of its four sides. Since opposite sides of a parallelogram are equal, the formula for the perimeter (P) can be given as:
P = 2(a + b)
where a and b represent the lengths of the two pairs of opposite sides.
Solved Examples on Area of Parallelogram
Let’s look at some examples of how to find the area of a parallelogram:
Example 1: A parallelogram has a base of 6 cm and a height of 4 cm. What is its area?
Using the formula A = b × h, we get A = 6 cm × 4 cm = 24 cm². So, the area of the parallelogram is 24 cm².
Example 2: A parallelogram has sides of lengths 8 cm and 10 cm, and the angle between the sides is 60 degrees. What is its area?
Using the formula A = a × b × sin(θ), we get A = 8 cm × 10 cm × sin(60°) = 80 cm². So, the area of the parallelogram is 80 cm².
How Kunduz Can Help You Learn How To Find The Area of Parallelogram?
Kunduz is an amazing tool for students who want to learn and understand mathematical concepts in a simplified and easy-to-understand manner. With Kunduz, you can get solutions to your questions and get detailed explanations from expert tutors. The app also provides step-by-step solutions to help you understand how to find the area of a parallelogram and other mathematical concepts. It’s a great platform to enhance your learning and achieve academic success.
Remember, understanding the concept of how to find the area of a parallelogram is not just about memorizing formulas. It’s about understanding the principles behind these formulas and knowing when and how to apply them. Practice and consistency are key to mastering this concept. Happy learning!
