Arithmetic sequences are an important concept in mathematics that involve a sequence of numbers where each term is obtained by adding a constant difference to the previous term. In this article, we will explore the definition, formulas, properties, and examples of arithmetic sequences, as well as answer frequently asked questions about them.
An Introduction to the Arithmetic Sequence
Sequences are ordered collections of objects that follow a specific pattern or rule. They are used in various mathematical and real-world applications. One type of sequence is the arithmetic sequence, where the difference between each pair of consecutive terms is constant. This constant difference is often referred to as the common difference.
Arithmetic sequences can be found in many different contexts, such as number patterns, financial calculations, and physics problems. Understanding the concept of arithmetic sequences and being able to apply the relevant formulas can be extremely useful in solving a wide range of mathematical problems.
What is an Arithmetic Sequence?
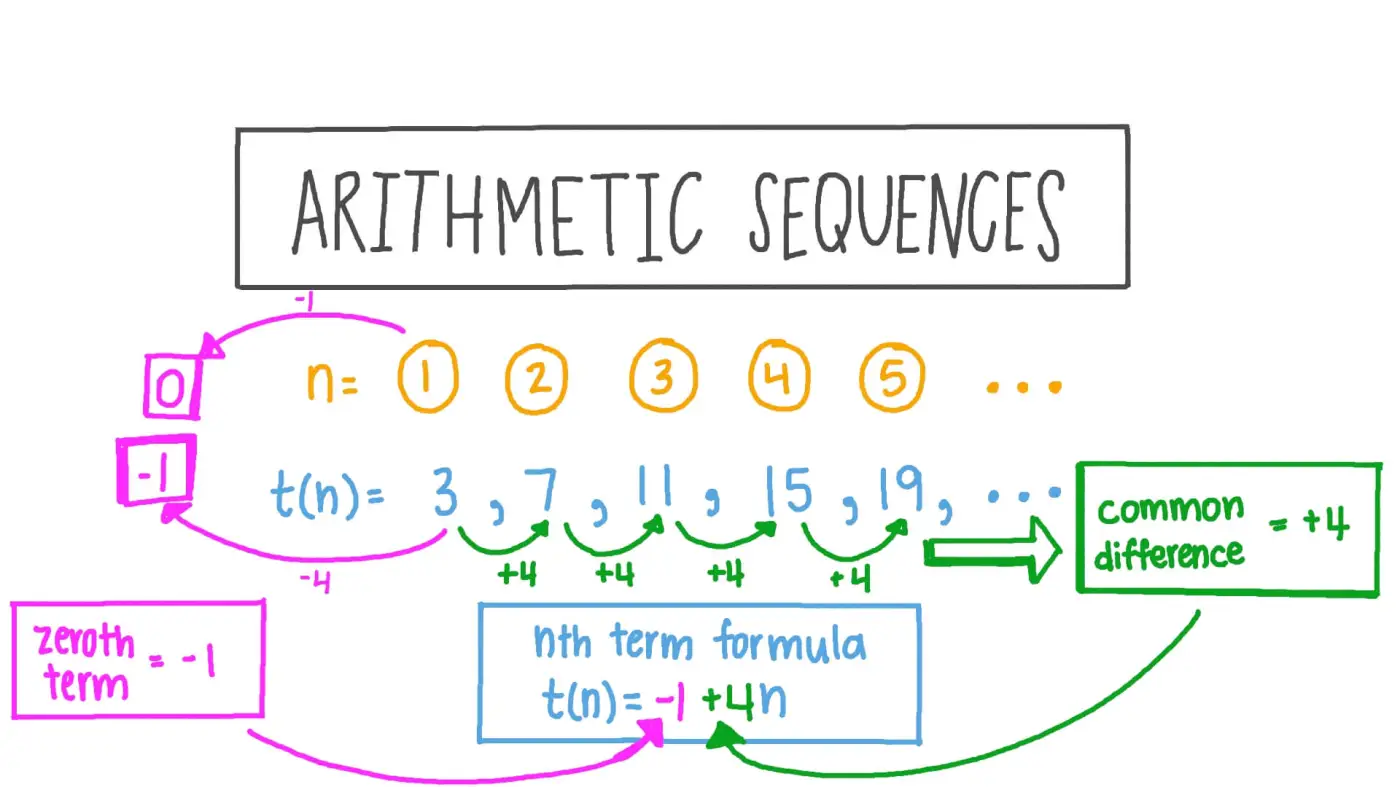
An arithmetic sequence is a sequence in which each term is obtained by adding a constant difference to the previous term. This means that the difference between any two consecutive terms in the sequence is always the same. The first term of the sequence is denoted as “a”, and the common difference is denoted as “d”.
The general form of an arithmetic sequence is: a, a + d, a + 2d, a + 3d, …
For example, consider the sequence 2, 4, 6, 8, 10, … In this sequence, the first term (a) is 2, and the common difference (d) is 2. Each term is obtained by adding 2 to the previous term.
Arithmetic Sequence Formulas
There are several important formulas associated with arithmetic sequences that can be used to find specific terms or calculate the sum of the terms in the sequence. These formulas include the nth term formula, the recursive formula, and the explicit formula.
Nth Term of Arithmetic Sequence
The nth term formula allows us to find the value of any term in an arithmetic sequence. It is given by the formula:
an = a + (n – 1)d
where:
- an represents the nth term of the sequence
- a is the first term of the sequence
- n is the position of the term in the sequence
- d is the common difference between terms
For example, let’s find the 5th term of the sequence 2, 4, 6, 8, 10, … Using the nth term formula, we have:
a = 2 d = 2 n = 5
an = 2 + (5 – 1) * 2 = 2 + 4 * 2 = 2 + 8 = 10
Therefore, the 5th term of the sequence is 10.
Recursive Formula for Arithmetic Sequence
The recursive formula is another way to find the nth term of an arithmetic sequence. It is based on the relationship between each term and the previous term. The recursive formula for an arithmetic sequence is:
an = an-1 + d
where:
- an represents the nth term of the sequence
- an-1 represents the (n – 1)th term of the sequence
- d is the common difference between terms
Using the recursive formula, we can find any term in the sequence by adding the common difference to the previous term. This formula can be especially useful when finding terms further down the sequence.
Explicit Formula for Arithmetic Sequence
The explicit formula, also known as the closed-form formula, provides a direct way to calculate the nth term of an arithmetic sequence without having to rely on previous terms. The explicit formula is given by:
an = a + (n – 1)d
This formula is similar to the nth term formula, but it does not require knowledge of the previous terms in the sequence. It can be used to find any term directly, making it a convenient formula to use in calculations.
Sum of Terms in Arithmetic Sequence
The sum of the terms in an arithmetic sequence, also known as the arithmetic series, can be calculated using the following formula:
S = (n/2)(a + l)
where:
- S represents the sum of the terms in the sequence
- n is the number of terms in the sequence
- a is the first term of the sequence
- l is the last term of the sequence
Alternatively, the sum of the terms can be calculated using the following formula:
S = (n/2)(2a + (n – 1)d)
This formula is derived by multiplying the average of the first and last terms by the number of terms. It provides a quick and efficient way to find the sum of arithmetic sequences.
Product
In addition to the nth term and sum formulas, arithmetic sequences also have formulas for the product of the terms. The product of the terms in an arithmetic sequence can be calculated using the following formula:
P = an / a
where:
- P represents the product of the terms in the sequence
- an is the nth term of the sequence
- a is the first term of the sequence
This formula allows us to find the product of the terms in the sequence without having to calculate each individual term.
Standard Deviation
The standard deviation is a measure of how spread out the terms in an arithmetic sequence are from the mean. It can be calculated using the following formula:
σ = √[(Σ(xi – x̄)^2) / N]
where:
- σ represents the standard deviation
- Σ(xi – x̄)^2 represents the sum of the squared differences between each term and the mean
- N represents the number of terms in the sequence
- √ represents the square root
The standard deviation provides valuable information about the variability of the terms in the sequence.
Derivation of Arithmetic Sequence Formula
The arithmetic sequence formula can be derived by considering the relationship between each term and the previous term. Let’s suppose we have an arithmetic sequence with the first term “a” and the common difference “d”. The second term of the sequence can be obtained by adding the common difference to the first term:
a2 = a1 + d
Similarly, the third term can be obtained by adding the common difference to the second term:
a3 = a2 + d
Continuing this pattern, we can express the nth term as follows:
an = an-1 + d
This recursive formula allows us to find any term in the sequence by adding the common difference to the previous term. By rearranging this formula, we can derive the explicit formula for the nth term:
an = a + (n – 1)d
This formula provides a direct way to calculate any term in the sequence without having to rely on previous terms.
Linear Sequences
Arithmetic sequences are an example of linear sequences, which are sequences that follow a linear pattern or rule. In a linear sequence, the difference between consecutive terms is always the same, resulting in a straight line when graphed. This linear relationship between terms makes arithmetic sequences relatively easy to work with and calculate.
Linear sequences can be found in various real-world situations, such as the growth of populations, the depreciation of assets, and the progression of time. Understanding the concept of linear sequences and being able to apply the relevant formulas can be useful in solving a wide range of mathematical and real-world problems.

Arithmetic Series
The sum of the terms in an arithmetic sequence is called an arithmetic series. The sum of an arithmetic series can be calculated using the following formula:
S = (n/2)(a + l)
where:
- S represents the sum of the terms in the series
- n is the number of terms in the series
- a is the first term of the series
- l is the last term of the series
This formula is derived by multiplying the average of the first and last terms by the number of terms. It provides a quick and efficient way to find the sum of arithmetic series.
For example, consider the arithmetic series 3, 6, 9, 12, 15. The first term (a) is 3, the last term (l) is 15, and the number of terms (n) is 5. Using the sum formula, we have:
S = (5/2)(3 + 15) = (5/2)(18) = 45
Therefore, the sum of the terms in the arithmetic series is 45.
Applications of Arithmetic Sequence Formula
Arithmetic sequences and their formulas have various applications in mathematics, science, finance, and other fields. Some common applications include:
- Number patterns: Arithmetic sequences are often used to identify and describe number patterns, such as counting by twos, threes, or other constant differences.
- Financial calculations: Arithmetic sequences can be used to calculate loan payments, compound interest, and other financial calculations.
- Physics problems: Arithmetic sequences are used to model various physical phenomena, such as the displacement of an object over time or the acceleration of a moving body.
- Mathematical series: Arithmetic sequences form the basis for arithmetic series, which are used to calculate the sum of a finite number of terms in a sequence.
- Algebraic equations: Arithmetic sequences can be used to solve algebraic equations and find the values of variables.
Understanding arithmetic sequences and their formulas allows us to solve a wide range of mathematical problems and make accurate calculations in various real-world situations.
Types of Arithmetic Sequence
While arithmetic sequences all follow the general rule of having a constant difference between terms, there are different types of arithmetic sequences based on the value of the common difference:
- Positive arithmetic sequence: In a positive arithmetic sequence, the common difference is a positive number. This means that each term is obtained by adding a positive value to the previous term.
- Negative arithmetic sequence: In a negative arithmetic sequence, the common difference is a negative number. This means that each term is obtained by subtracting a positive value from the previous term.
- Zero arithmetic sequence: In a zero arithmetic sequence, the common difference is zero. This means that each term is the same as the previous term, as there is no change or progression.
- Fractional arithmetic sequence: In a fractional arithmetic sequence, the common difference is a fraction. This means that each term is obtained by adding or subtracting a fraction from the previous term.
Each type of arithmetic sequence exhibits specific patterns and properties based on the value of the common difference.
Properties of Arithmetic Sequence
Arithmetic sequences have several important properties that make them unique and useful in mathematical calculations. Some key properties of arithmetic sequences include:
- Common difference: The common difference is a constant value that determines the difference between each pair of consecutive terms in the sequence.
- Linear relationship: Arithmetic sequences exhibit a linear relationship between terms, resulting in a straight line when graphed.
- Constant rate of change: The common difference represents the constant rate of change between consecutive terms. It is the amount by which each term changes compared to the previous term.
- Symmetry around the mean: Arithmetic sequences exhibit symmetry around the mean or average of the terms. The terms on one side of the mean are mirror images of the terms on the other side.
- Additive inverses: In an arithmetic sequence, each term has an additive inverse or opposite term. Adding the common difference to a term results in the next term, while subtracting the common difference from a term results in the previous term.
Understanding these properties can help in identifying and analyzing arithmetic sequences, as well as making calculations and predictions based on the patterns they exhibit.
Difference Between Arithmetic Sequence and Geometric Sequence
While arithmetic sequences involve adding a constant difference to each term, geometric sequences involve multiplying each term by a constant ratio. The key differences between arithmetic sequences and geometric sequences are as follows:
- Arithmetic Sequence: In an arithmetic sequence, the difference between any two consecutive terms is constant. The terms are obtained by adding a fixed value to the previous term. For example, the sequence 2, 4, 6, 8, 10 is an arithmetic sequence with a common difference of 2.
- Geometric Sequence: In a geometric sequence, the ratio between any two consecutive terms is constant. The terms are obtained by multiplying the previous term by a fixed value. For example, the sequence 2, 6, 18, 54, 162 is a geometric sequence with a common ratio of 3.
Arithmetic and geometric sequences have different patterns and relationships between terms, leading to different formulas and properties for each type of sequence. Understanding the differences between the two can help in solving problems and analyzing sequences in different contexts.
| Property | Arithmetic Sequence | Geometric Sequence |
|---|---|---|
| Relationship between terms | Addition of a constant difference | Multiplication by a constant ratio |
| Common difference/ratio | Fixed constant | Fixed constant |
| Formula for nth term | an = a + (n – 1)d | an = a * r^(n-1) |
| Formula for sum of terms | S = (n/2)(a + l) | S = a * (1 – r^n)/(1 – r) |
| Linear relationship | Yes | No |
| Constant rate of change | Yes | Yes |
| Symmetry around the mean | Yes | No |
| Additive/multiplicative inverses | Yes | Yes |
Understanding the differences between arithmetic and geometric sequences can help in identifying and solving problems involving these types of sequences.
Frequently Asked Questions on Arithmetic Sequence
What is an Arithmetic Sequence in Mathematics?
An arithmetic sequence in mathematics is a sequence of numbers in which the difference between any two consecutive terms is constant.
What are the formulas related to an Arithmetic Sequence?
The formulas related to an arithmetic sequence include the formula for the nth term, the recursive formula, and the formula for the sum of the terms.
What is the difference between an Arithmetic Sequence and an Arithmetic Series?
An arithmetic sequence is a collection of numbers where the difference between consecutive terms is constant. An arithmetic series, on the other hand, is the sum of the terms of an arithmetic sequence.
How do I identify an Arithmetic Sequence?
An arithmetic sequence can be identified by examining the difference between consecutive terms. If this difference is constant, the sequence is arithmetic.
How do I find the nth term of an Arithmetic Sequence?
The nth term of an arithmetic sequence can be found using the formula an = a + (n-1)d, where an is the nth term, a is the first term, n is the term number, and d is the common difference.
Solved Examples on Arithmetic Sequence
Example 1: Find the 15th term in the arithmetic sequence 0, 2, 4, 6, 8, 10, 12, 14…
Solution: In this sequence, the first term (a) is 0, and the common difference (d) is 2. Using the nth term formula, we have:
an = a + (n – 1)d a15 = 0 + (15 – 1) * 2 a15 = 0 + 14 * 2 a15 = 0 + 28 a15 = 28
Therefore, the 15th term in the sequence is 28.
Example 2: Find the sum of the first 12 odd natural numbers.
Solution: The sequence of the first 12 odd natural numbers is 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23. This is an arithmetic sequence with a common difference of 2 (each term is obtained by adding 2 to the previous term). Using the sum formula, we have:
S = (12/2)(1 + 23) S = 6(24) S = 144
Therefore, the sum of the first 12 odd natural numbers is 144.
How Can Kunduz Help You Learn Arithmetic Sequences?
At Kunduz, we understand the importance of mastering arithmetic sequences and their formulas. That’s why we offer a wide range of resources and tools to help you learn and excel in this topic.
Our comprehensive arithmetic sequence calculator allows you to quickly find the nth term, sum of terms, and other important calculations. Simply input the necessary values, and our calculator will do the rest.
In addition to our calculator, we provide detailed step-by-step explanations and examples to help you understand the concepts and apply them to various problems. Our expert tutors are also available to provide personalized assistance and guidance, ensuring that you have all the support you need to succeed.
Whether you’re studying for an exam, preparing for a math competition, or simply looking to improve your math skills, Kunduz is here to help. With our user-friendly resources and expert guidance, you’ll gain a deep understanding of arithmetic sequences and be well-equipped to tackle any problem that comes your way.
Mastering arithmetic sequences is an essential step in building a strong foundation in mathematics. Start exploring our resources today and take your math skills to the next level with Kunduz.
