In the realm of mathematics, asymptotes play a crucial role in understanding the behavior and tendencies of curves. An asymptote is a straight line that a curve approaches but never intersects. It serves as a guide in graphing functions and helps us understand what lines the curve should not touch. Asymptotes can be horizontal, vertical, or slant (oblique), each with its own characteristics and equations. In this article, we will delve into the definition of asymptotes, explore their different types, learn how to find them, and provide examples for better comprehension.
For those exploring the asymptotes and interested in diverse mathematical concepts, our hyperbolic functions and explicit formula pages serve as enriching references. These resources delve into advanced mathematical topics.
What is Asymptote?
An asymptote is a line that a curve approaches as it moves towards infinity. It is a line that the graph of a function converges to but never touches. Asymptotes are imaginary lines that help us understand the behavior of a curve and determine its limits. They can be horizontal, vertical, or slant, depending on the direction in which the curve approaches. Asymptotes are crucial in graphing functions accurately and understanding their characteristics.

How to Find Asymptotes?
Finding asymptotes involves determining the equations of the lines that the curve approaches. The method varies depending on the type of asymptote (horizontal, vertical, or slant). We will explore each type in detail and discuss the rules and techniques to find them.
How to Find Horizontal Asymptotes?
Horizontal asymptotes are lines that a curve approaches as the x-values tend to infinity or negative infinity. To find horizontal asymptotes, we consider the degrees of the polynomials in the numerator and denominator of the function.
- If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is at y = 0.
- If the degrees of the numerator and denominator are equal, divide the coefficients of the leading terms to find the horizontal asymptote.
- If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.
By following these rules, we can easily determine the horizontal asymptotes of a rational function.
Finding Horizontal Asymptotes of a Rational Function
Rational functions are functions with polynomials in the numerator and denominator. To find the horizontal asymptotes of a rational function, we compare the degrees of the numerator and denominator.
- If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0.
- If the degrees of the numerator and denominator are equal, divide the coefficients of the leading terms to find the horizontal asymptote.
- If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.
By following these rules, we can determine the horizontal asymptotes of a rational function.
How to Find Vertical Asymptotes?
Vertical asymptotes are lines that a curve approaches as the y-values tend to infinity or negative infinity. To find vertical asymptotes, we analyze the behavior of the function as x approaches certain values.
- Simplify the function to its lowest terms.
- Set the denominator equal to zero and solve for x to find the values where vertical asymptotes occur.
The x-values that make the denominator zero represent the vertical asymptotes of the function. By following these steps, we can easily determine the vertical asymptotes of a rational function.
Finding Vertical Asymptotes of a Rational Function
To find the vertical asymptotes of a rational function, we follow these steps:
- Simplify the function to its lowest terms.
- Set the denominator equal to zero and solve for x.
- The x-values where the denominator is zero represent the vertical asymptotes of the function.
By applying these steps, we can find the vertical asymptotes of a rational function.
How to Find Slant Asymptotes?
Slant asymptotes, also known as oblique asymptotes, occur when the degree of the numerator is exactly one more than the degree of the denominator. To find slant asymptotes, we use long division to divide the numerator by the denominator.
- Divide the numerator by the denominator using long division.
- The quotient obtained by the division, ignoring the remainder, gives the equation of the slant asymptote.
By following these steps, we can find the equation of the slant asymptote of a rational function.
How to Find Asymptotes of a Curve
To find the asymptotes of a curve, we consider the behavior of the curve as it approaches infinity. This involves analyzing the limits of the function as x or y tends to infinity or negative infinity. By evaluating these limits, we can determine the equations of the asymptotes that the curve approaches.
Types of Asymptotes
Asymptotes can be classified into three types: horizontal, vertical, and slant (oblique). Each type has its own characteristics and equations. Let’s explore each type in more detail.
Horizontal Asymptote
A horizontal asymptote is a horizontal line that a curve approaches as x tends to infinity or negative infinity. It represents the values that the function approaches as x becomes significantly large or small. The equation of a horizontal asymptote is of the form y = k, where k is a constant.
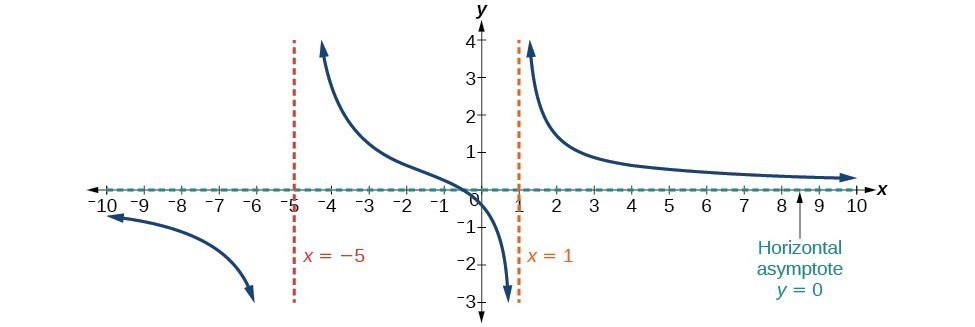
Vertical Asymptote
A vertical asymptote is a vertical line that a curve approaches as x approaches a certain value. It represents the restricted values of x throughout the function. The equation of a vertical asymptote is of the form x = a, where a is a constant.
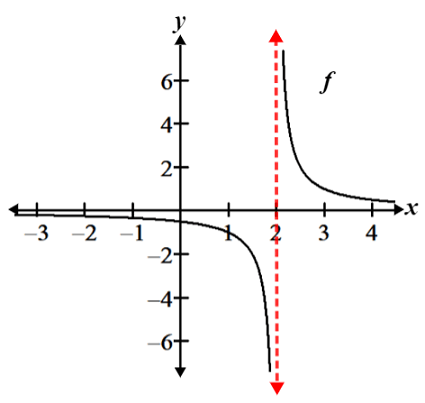
Slant Asymptote
A slant asymptote, also known as an oblique asymptote, is a slanted line that a curve approaches as x tends to infinity or negative infinity. It occurs when the degree of the numerator is exactly one more than the degree of the denominator. The equation of a slant asymptote is of the form y = mx + b, where m and b are constants.

Horizontal Asymptotes vs. Vertical Asymptotes vs. Slant Asymptote
Horizontal, vertical, and slant asymptotes have distinct characteristics that differentiate them from one another. Let’s compare these types of asymptotes in the table below:
| Asymptote Type | Equation | Behavior |
|---|---|---|
| Horizontal | y = k | Curve approaches a constant value |
| Vertical | x = a | Curve approaches infinity or -infinity |
| Slant | y = mx + b | Curve approaches a slanted line |
Understanding the differences between horizontal, vertical, and slant asymptotes allows us to accurately analyze the behavior of curves and graph functions.
Characteristics of Asymptotes
Asymptotes have several important characteristics that help us understand their behavior and significance in graphing functions. Here are some key characteristics of asymptotes:
- Asymptotes are lines that curves approach but never intersect.
- They guide the behavior of the curve as it moves towards infinity.
- Asymptotes can be horizontal, vertical, or slant, depending on the direction of approach.
- Horizontal asymptotes represent the values that the function approaches as x tends to infinity or negative infinity.
- Vertical asymptotes represent the restricted values of x throughout the function.
- Slant asymptotes occur when the degree of the numerator is one more than the degree of the denominator.
- Asymptotes provide valuable information about the limits and tendencies of curves.
By understanding these characteristics, we can utilize asymptotes to accurately graph functions and analyze their behavior.
Asymptote Formula
The formulas for asymptotes depend on the type of asymptote. Let’s explore the formulas for each type:
Horizontal Asymptote Formula
The equation of a horizontal asymptote is of the form y = k, where k is a constant. It represents the value that the function approaches as x tends to infinity or negative infinity.
Vertical Asymptote Formula
The equation of a vertical asymptote is of the form x = a, where a is a constant. It represents the values of x where the function approaches infinity or negative infinity.
Oblique Asymptote Formula
The equation of an oblique or slant asymptote is of the form y = mx + b, where m and b are constants. It occurs when the degree of the numerator is one more than the degree of the denominator.
Hyperbola Asymptote Formula
For a hyperbola, the equation of asymptotes depends on the center of the hyperbola. If the center is located at the origin, the equations of the asymptotes are y = ±(b/a)x.
By utilizing these formulas, we can easily determine the equations of asymptotes for different types of curves.
Solved Examples on Asymptotes
Let’s explore some examples to better understand how to find asymptotes:
Example 1: Find the horizontal asymptote for the function f(x) = (3x – 2)/(x + 1).
Solution: To find the horizontal asymptote, we compare the degrees of the numerator and denominator. In this case, the degree of the numerator is equal to the degree of the denominator.
By dividing the coefficients of the leading terms, we find that the horizontal asymptote is y = 3.
Example 2: Find the vertical asymptote for the function f(x) = (x^2 + 3)/(x + 1).
Solution: To find the vertical asymptote, we set the denominator equal to zero and solve for x.
By solving (x + 1) = 0, we find that the vertical asymptote is x = -1.
Example 3: Find the slant asymptote for the function f(x) = (2x^2 + 3x – 1)/(x + 2).
Solution: To find the slant asymptote, we perform long division of the numerator by the denominator.
By dividing (2x^2 + 3x – 1) by (x + 2), we get a quotient of 2x – 7.
Therefore, the slant asymptote is y = 2x – 7.
By solving these examples, we can see how to find different types of asymptotes and understand their significance in graphing functions.
How Kunduz Can Help You Learn Asymptotes?
At Kunduz, we understand the importance of understanding asymptotes in mathematics. Our comprehensive learning materials and expert instructors can guide you through the concept of asymptotes, helping you grasp the fundamentals and apply them to various mathematical problems. With our step-by-step explanations and engaging examples, you can build a strong foundation in asymptotes and excel in your mathematical journey.
Whether you’re a student seeking clarification or an educator looking for valuable teaching resources, Kunduz is here to support you. Our user-friendly platform provides access to a wealth of educational materials, including video tutorials, practice exercises, and personalized guidance. Join Kunduz today and embark on a rewarding learning experience centered around mastering asymptotes and achieving academic success.
