The Boltzmann constant is a fundamental constant in physics and is denoted by the symbol kB or k. It relates the average kinetic energy of gas particles to the temperature of the gas. This constant plays a crucial role in statistical mechanics and thermodynamics, providing a bridge between microscopic and macroscopic properties of matter.
The Boltzmann constant is named after Ludwig Boltzmann, an Austrian physicist who made significant contributions to the field of statistical mechanics in the 19th century. It was introduced by Max Planck as a means to connect the gas constant and Avogadro’s number.
What is the Boltzmann Constant?
The Boltzmann constant is a vital element in the proportional correlation between the average kinetic energy of gas particles and the gas’s temperature. Introduced by Max Planck and named after Ludwig Boltzmann, it is a physical constant that is calculated by taking the ratio of two other constants, namely the gas constant and Avogadro’s number.

The Formula of the Boltzmann Constant
The Boltzmann constant’s value is mathematically expressed through a simple formula:
k = R/NA
In this formula, k denotes Boltzmann’s constant, R stands for the gas constant, and NA signifies Avogadro’s number.
History of Boltzmann’s Constant
The Boltzmann constant is named after Ludwig Boltzmann, an Austrian physicist who made significant contributions to the field of statistical mechanics in the 19th century. Boltzmann was known for his work on the statistical interpretation of the second law of thermodynamics and the development of the Boltzmann equation.
Although Boltzmann first linked probability and entropy in 1877, the specific constant relating the two was not introduced until Max Planck’s work. Planck gave the constant the symbol “k” and provided a more precise and accurate value for it.
The Boltzmann constant became an essential part of statistical mechanics and thermodynamics, allowing for the understanding of the relationship between microscopic and macroscopic properties of matter.
Experimental Determination of Boltzmann’s Constant
The Boltzmann constant can be determined experimentally using various methods. One of the most common methods is based on the measurement of Brownian motion, which is the random motion of particles suspended in a fluid.
By observing the Brownian motion of particles, researchers can determine the diffusion coefficient of the particles and use it to calculate the Boltzmann constant. This method relies on the relationship between the diffusion coefficient, temperature, and the Boltzmann constant.
Other experimental techniques involve measuring the heat capacity of gases and the specific heat of solids. These measurements can provide valuable data for calculating the Boltzmann constant.
Over the years, numerous experiments have been conducted to determine the value of the Boltzmann constant with increasing precision. These measurements have contributed to our understanding of fundamental physics and have helped validate the theoretical predictions of statistical mechanics.

Value of Boltzmann Constant
The value of the Boltzmann constant is approximately 1.380649 × 10⁻²³ joules per Kelvin (J/K). This value is derived from the relationship between the gas constant (R) and Avogadro’s number (NA).
The Boltzmann constant can also be expressed in other units, such as electron volts per Kelvin (eV/K), ergs per Kelvin (erg/K), or reciprocal centimeters per Kelvin (cm-1/K).
Here are the values of the Boltzmann constant in different units:
- Boltzmann constant (J/K): 1.380649 × 10⁻²³ J/K
- Boltzmann constant (eV/K): 8.617333262145 × 10⁻⁵ eV/K
- Boltzmann constant (erg/K): 1.380649 × 10⁻¹⁶ erg/K
- Boltzmann constant (cm^-1/K): 0.69503477 cm-1/K
These values are essential for calculations and equations involving temperature, energy, and entropy in various branches of physics.
Value Of k (Value Of k and Units Table)
The value of the Boltzmann constant, denoted as k, depends on the units in which it is expressed. Here is a table showing the value of k in different units:
| Units | Value of k (Boltzmann constant) |
|---|---|
| J/K | 1.380649 × 10⁻²³ J/K |
| eV/K | 8.617333262145 × 10⁻⁵ eV/K |
| erg/K | 1.380649 × 10⁻¹⁶ erg/K |
| cm-1/K | 0.69503477 cm^-1/K |
These values are used in various calculations and equations in physics, chemistry, and other scientific disciplines.
Boltzmann Constant Units
The Boltzmann constant is represented in units of energy divided by temperature. In SI units, it is expressed as Joules per Kelvin (J/K). In other units, it can be expressed as electron volts per Kelvin (eV/K), ergs per Kelvin (erg/K), or other similar units, depending on the context.
Applications of Boltzmann Constant
The Boltzmann constant is used in various branches of physics and chemistry due to its fundamental role in relating temperature and energy. Some of the key applications of the Boltzmann constant are:
- Statistical Mechanics: The Boltzmann constant is an essential component of statistical mechanics, which describes the behavior of large systems of particles based on their microscopic properties. It is used to calculate the probability distribution of particle energies and determine the equilibrium properties of systems.
- Thermodynamics: The Boltzmann constant plays a crucial role in the field of thermodynamics, which studies the relationships between heat, work, and energy. It is used in equations such as the ideal gas law, which relates the pressure, volume, and temperature of a gas.
- Entropy: The Boltzmann constant is used in the statistical definition of entropy, a fundamental concept in thermodynamics. Entropy measures the degree of disorder or randomness in a system and is related to the number of possible microstates corresponding to a given macrostate.
- Kinetic Theory of Gases: The Boltzmann constant is used in the kinetic theory of gases to relate the average kinetic energy of gas particles to the temperature of the gas. It helps explain phenomena such as pressure, temperature, and volume relationships in gases.
- Semiconductor Physics: In semiconductor physics, the Boltzmann constant is used to express thermal voltage, which is the voltage produced across a p-n junction due to a temperature difference. It is also used in equations related to carrier concentration and diffusion in semiconductors.
- Chemical Kinetics: The Boltzmann constant is employed in chemical kinetics to calculate the rate constants of chemical reactions. It appears in equations such as the Eyring equation and the Arrhenius equation, which describe the temperature dependence of reaction rates.
These are just a few examples of the wide range of applications of the Boltzmann constant in various fields of science. Its significance lies in its ability to connect microscopic and macroscopic properties of matter and provide insights into the behavior of particles and systems.
Solved Examples On Boltzmann Constant
To further illustrate the applications of the Boltzmann constant, let’s consider a few solved examples:
Example 1: Calculation of Boltzmann Constant in eV/K
Given the value of the Boltzmann constant in joules per Kelvin (J/K), calculate its value in electron volts per Kelvin (eV/K).
Solution: To convert from joules to electron volts, we need to divide the Boltzmann constant by the conversion factor of 1.602176634 × 10⁻¹⁹ J/eV.
kB (in eV/K) = (1.380649 × 10⁻²³ J/K) / (1.602176634 × 10⁻¹⁹ J/eV) ≈ 8.617333262145 × 10⁻⁵ eV/K
Therefore, the Boltzmann constant in electron volts per Kelvin is approximately 8.617333262145 × 10⁻⁵ eV/K.
Example 2: Calculation of Boltzmann Constant in cm^-1/K
Given the value of the Boltzmann constant in joules per Kelvin (J/K), calculate its value in reciprocal centimeters per Kelvin (cm-1/K).
Solution: To convert from joules to reciprocal centimeters, we need to divide the Boltzmann constant by the conversion factor of 1.986445857 × 10-23 J/cm-1.
kB (in cm-1/K) = (1.380649 × 10⁻²³ J/K) / (1.986445857 × 10⁻²³ J/cm^-1) ≈ 0.69503477 cm^-1/K
Therefore, the Boltzmann constant in reciprocal centimeters per Kelvin is approximately 0.69503477 cm^-1/K.
These examples demonstrate how the Boltzmann constant can be converted into different units depending on the specific requirements of the problem or application.
Boltzmann Constant and Ideal Gas Equation
The Boltzmann constant is closely related to the ideal gas equation, which describes the behavior of an ideal gas in terms of its pressure, volume, and temperature. The ideal gas equation is given by:
PV = nRT
Where:
- P is the pressure of the gas,
- V is the volume of the gas,
- n is the number of moles of the gas,
- R is the gas constant, and
- T is the temperature of the gas.
The gas constant (R) is related to the Boltzmann constant (kB) and Avogadro’s number (NA) through the equation:
R = kB * NA
By substituting this relationship into the ideal gas equation, we can express the equation using the Boltzmann constant:
PV = (n * kB * NA) * T
Simplifying further, we obtain:
PV = N * kB * T
Where N is the number of gas particles (N = n * NA).
This form of the ideal gas equation highlights the role of the Boltzmann constant in relating the macroscopic properties of an ideal gas (pressure and volume) to its temperature and the number of gas particles.
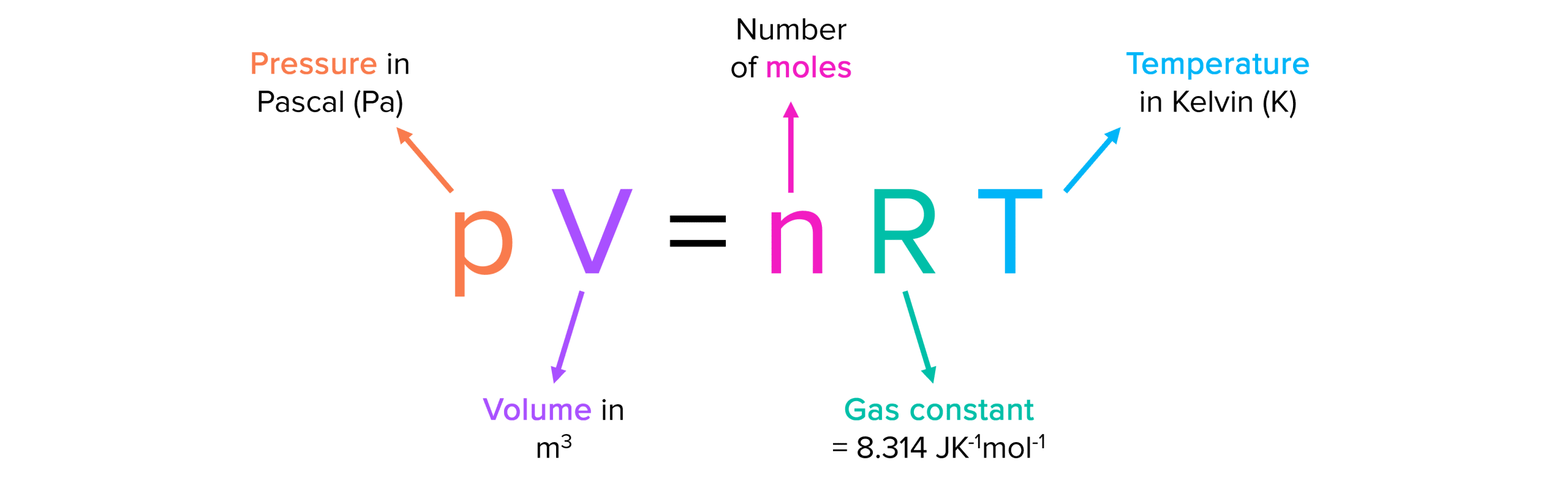
Boltzmann Constant in Chemical Kinetics
The Boltzmann constant plays a significant role in chemical kinetics, which is the study of the rates of chemical reactions. It appears in equations that describe the temperature dependence of reaction rates, such as the Eyring equation and the Arrhenius equation.
Eyring Equation
The Eyring equation relates the rate constant (k) of a chemical reaction to temperature (T), the Gibbs energy of activation (ΔG‡), the gas constant (R), and the Planck constant (h). The equation is given by:
k = (κ * kB * T * e^(-ΔG‡ / (R * T))) / h
Where:
- κ is the transmission coefficient,
- kB is the Boltzmann constant,
- T is the absolute temperature,
- ΔG‡ is the Gibbs energy of activation,
- R is the gas constant, and
- h is the Planck constant.
The Eyring equation allows us to calculate the rate constant of a chemical reaction based on the temperature and the energy barrier required for the reaction to proceed.
Arrhenius Equation
The Arrhenius equation is another equation used in chemical kinetics to describe the temperature dependence of reaction rates. It relates the rate constant (k) to the pre-exponential factor (A), the activation energy (Ea), the Boltzmann constant (kB), and the absolute temperature (T). The equation is given by:
k = A * e^(-Ea / (kB * T))
Where:
- A is the pre-exponential factor,
- Ea is the activation energy,
- kB is the Boltzmann constant, and
- T is the absolute temperature.
The Arrhenius equation allows us to calculate the rate constant of a chemical reaction at different temperatures, providing insights into the temperature dependence of the reaction rate.
These equations demonstrate the significance of the Boltzmann constant in chemical kinetics, where it is used to relate temperature to the rates of chemical reactions.

The Boltzmann Constant in Statistical Mechanics
Statistical mechanics is a branch of physics that provides a framework for understanding the behavior of large systems of particles based on their microscopic properties. The Boltzmann constant plays a fundamental role in statistical mechanics, connecting the macroscopic properties of a system to the microscopic behavior of its constituent particles.
A Degree of Freedom
The Boltzmann constant is used to define the average thermal energy carried by each microscopic degree of freedom in a thermodynamic system at absolute temperature (T). The average thermal energy associated with each degree of freedom is equal to 1/2 * kB * T.
A degree of freedom represents an independent way in which a particle can store energy. For example, in a monatomic gas, each atom has three degrees of freedom corresponding to its motion along three spatial dimensions (x, y, z). In this case, the average thermal energy associated with each degree of freedom is 1/2 * kB * T.
Kinetic Theory of Gases
The kinetic theory of gases describes the behavior of gas particles based on the principles of Newtonian mechanics and statistical mechanics. The Boltzmann constant is used in the kinetic theory of gases to relate the average kinetic energy of gas particles to the temperature of the gas.
According to the kinetic theory of gases, the average kinetic energy (KE) of a gas particle is directly proportional to the temperature (T) of the gas. Mathematically, this relationship can be expressed as:
KE = 3/2 * kB * T
Where:
- KE is the average kinetic energy of a gas particle,
- kB is the Boltzmann constant, and
- T is the temperature of the gas.
This equation shows that as the temperature of a gas increases, the average kinetic energy of its particles also increases. The Boltzmann constant provides a quantitative measure of the relationship between kinetic energy and temperature in the kinetic theory of gases.
Partition Function
In statistical mechanics, the partition function (Z) plays a central role in determining the thermodynamic properties of a system. The partition function is defined as the sum of the Boltzmann factors of all possible microstates of a system.
The Boltzmann factor is given by:
e^(-E / (kB * T))
Where:
- E is the energy of a particular microstate,
- kB is the Boltzmann constant, and
- T is the temperature of the system.
The partition function is mathematically expressed as:
Z = Σ(e^(-E / (kB * T)))
Where the sum (Σ) is taken over all possible microstates of the system.
The partition function is used to calculate various thermodynamic quantities, such as the Helmholtz free energy, entropy, and internal energy of a system.
Statistical Entropy
The Boltzmann constant is also involved in the statistical definition of entropy, a fundamental concept in thermodynamics. The statistical entropy (S) is defined as the natural logarithm of the number of microstates (W) corresponding to a given macrostate:
S = kB * ln(W)
Where:
- S is the statistical entropy,
- kB is the Boltzmann constant, and
- W is the number of microstates.
The statistical entropy provides a measure of the disorder or randomness of a system. It is related to the thermodynamic entropy, which is a macroscopic property associated with the heat transfer and energy distribution in a system.
The Boltzmann constant is crucial in the statistical definition of entropy, allowing for the connection between microscopic behavior and macroscopic properties of matter.
Method for Calculating the Boltzmann Constant
The Boltzmann constant can be determined experimentally using several methods. One common approach is based on the measurement of Brownian motion, which is the random motion of particles suspended in a fluid.
By observing the Brownian motion of particles, researchers can determine the diffusion coefficient of the particles, which is related to the Boltzmann constant. This method relies on the relationship between the diffusion coefficient, temperature, and the Boltzmann constant.
Another experimental technique involves measuring the heat capacity of gases or the specific heat of solids. These measurements provide valuable data for calculating the Boltzmann constant.
In recent years, numerous experiments have been conducted to determine the value of the Boltzmann constant with increasing precision. These measurements have contributed to our understanding of fundamental physics and have helped validate the predictions of statistical mechanics.
Significance of the Boltzmann Distribution
The Boltzmann distribution is a probability distribution that describes the distribution of particle energies in a system at thermal equilibrium. It is derived from the principles of statistical mechanics and is based on the Boltzmann factor, which is given by:
e^(-E / (kB * T))
Where:
- E is the energy of a particular state,
- kB is the Boltzmann constant, and
- T is the temperature of the system.
The Boltzmann distribution allows us to calculate the probability of a particle occupying a particular energy state at a given temperature. It provides insights into the thermal equilibrium and the statistical behavior of particles in a system.
The Boltzmann distribution is used in various fields, including physics, chemistry, and biology, to analyze and predict the behavior of systems at the microscopic level. It is a fundamental concept in statistical mechanics and provides a basis for understanding the macroscopic properties of matter.
What is the value of Boltzmann constant in eV?
The value of the Boltzmann constant in electron volts per Kelvin (eV/K) is approximately 8.617333262145 × 10⁻⁵ eV/K.
The Boltzmann constant can be expressed in different units depending on the context and application. In electron volts per Kelvin, it represents the energy associated with each degree of freedom of a particle in a system at a given temperature.
The conversion from joules to electron volts involves dividing the Boltzmann constant by the conversion factor of 1.602176634 × 10⁻¹⁹ J/eV.
The value of the Boltzmann constant in eV/K is commonly used in particle physics, semiconductor physics, and other fields where energy levels and temperature are significant factors.
Conclusion
The Boltzmann constant, denoted by kB or k, is a fundamental constant in physics that relates the average kinetic energy of gas particles to the temperature of the gas. It plays a crucial role in statistical mechanics, thermodynamics, and various other branches of science.
The Boltzmann constant is named after Ludwig Boltzmann, an Austrian physicist who made significant contributions to the field of statistical mechanics. It is derived by dividing the gas constant (R) by Avogadro’s number (NA).
The Boltzmann constant has various units of measurement, including joules per Kelvin (J/K), electron volts per Kelvin (eV/K), ergs per Kelvin (erg/K), and reciprocal centimeters per Kelvin (cm-1/K). These units are used in different branches of science and depend on the specific context and application.
The Boltzmann constant is utilized in statistical mechanics, thermodynamics, chemical kinetics, and semiconductor physics, among other fields. It is involved in equations such as the ideal gas law, Eyring equation, Arrhenius equation, and the statistical definition of entropy.
Experimental determination of the Boltzmann constant is achieved through methods such as measuring Brownian motion and heat capacity. These measurements contribute to our understanding of fundamental physics and validate theoretical predictions.
The Boltzmann constant provides a bridge between the microscopic and macroscopic properties of matter, allowing for the quantification of temperature, energy, and entropy. Its significance lies in its ability to connect the behavior of individual particles to the behavior of larger systems, providing insights into the fundamental nature of the universe.
