A coordinate plane, also known as a Cartesian plane, is a fundamental concept in the fields of mathematics and physics. It is a two-dimensional space where points are plotted and located using an ordered pair of numbers, also known as coordinates.
These coordinates provide the exact position of a point on the plane relative to a central point known as the origin. The coordinate plane is divided into four sections known as quadrants, which are labeled using Roman numerals (I, II, III, IV).
The coordinate plane is an essential tool in various branches of science, engineering, computer graphics, and even in navigation and planning.
What is the Coordinate Plane?
A coordinate plane is formulated by the intersection of two perpendicular lines, referred to as the axes. The horizontal line is known as the x-axis, while the vertical line is the y-axis.
The point of intersection of these axes, (0,0), is called the origin. Each point on the plane is represented by a pair of numbers (x, y), where ‘x’ represents the horizontal distance and ‘y’ represents the vertical distance from the origin.

Quadrants on a Coordinate Plane
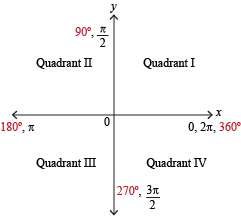
The intersection of the x and y axes divides the coordinate plane into four quadrants.
- Quadrant I: Here, both x and y coordinates are positive.
- Quadrant II: The x coordinates are negative, while the y coordinates are positive.
- Quadrant III: Both x and y coordinates are negative.
- Quadrant IV: Here, x coordinates are positive, and y coordinates are negative.
This arrangement of quadrants is in a counterclockwise direction.
Locating a Point on the Coordinate Plane
The location of any point on the coordinate plane is described by an ordered pair of numbers (x, y). The first number ‘x’ is the x-coordinate or abscissa, and the second number ‘y’ is the y-coordinate or ordinate.
To locate a point:
- Start at the origin.
- Move along the x-axis the number of units indicated by the x-coordinate.
- From this point, move parallel to the y-axis the number of units indicated by the y-coordinate.
- Mark the final position. This is the location of the point on the coordinate plane.
Plotting Points on a Coordinate Plane
To plot a point on the coordinate plane, we use the coordinates of the point. For example, to plot the point P(2,3):
- Start at the origin.
- Move 2 units to the right on the x-axis.
- From this point, move 3 units upwards parallel to the y-axis.
- Mark the point P at this location. P(2,3) is in the first quadrant.
The process is the same for points in other quadrants, but direction of movement along the axes will change according to the signs of the coordinates.
Properties Of Coordinate Plane
Axes
The coordinate plane consists of two axes that intersect each other at a right angle at the origin. The horizontal line is the x-axis, and the vertical line is the y-axis.
Origin
The origin is the point (0,0) where the x-axis and y-axis intersect. It is the reference point for defining all other points on the coordinate plane.
Cartesian Plane Quadrants
The cartesian plane is divided into four quadrants by the x and y axes. Each quadrant has unique characteristics based on the signs of x and y coordinates.
Cartesian Coordinates
Each point on the cartesian plane is represented by a pair of numbers (x, y), known as cartesian coordinates. The x-coordinate represents the horizontal position, and the y-coordinate represents the vertical position of the point.
Abscissa
The abscissa of a point is its x-coordinate. It represents the horizontal distance of the point from the origin.
Ordinate
The ordinate of a point is its y-coordinate. It represents the vertical distance of the point from the origin.
One Dimensional Plane
A one-dimensional plane, also known as a number line, only has one axis, typically the x-axis. Every point on this line can be represented by a single number, which is its distance from the origin.
Two Dimensional Plane
A two-dimensional plane, such as the Cartesian plane, has two axes, the x-axis and the y-axis. Every point on this plane is represented by an ordered pair of numbers (x, y), which are its distances from the origin along the x-axis and the y-axis.
Three Dimensional Plane
A three-dimensional plane, also known as a Cartesian space, has three axes: the x-axis, the y-axis, and the z-axis. Every point in this space is represented by an ordered triple of numbers (x, y, z), which are its distances from the origin along the three axes.
Cartesian Representation of Complex Numbers
In the Cartesian coordinate system, complex numbers can be represented as points. A complex number z = a + ib can be represented as a point (a, b) in the plane, where ‘a’ is the real part and ‘b’ is the imaginary part.
How to Plot the points in the Cartesian plane?
To plot a point in the Cartesian plane, we need to first identify its coordinates. We then move horizontally from the origin to the x-coordinate and then vertically to the y-coordinate. The intersection of these movements is the location of the point.
Graphing on the Cartesian Coordinate Plane
The Cartesian coordinate plane is used extensively for graphing functions and equations. To graph a function, we plot a set of points whose coordinates satisfy the function, and then connect these points to form a curve.
Computing the Midpoint of Two Points
The coordinates of the midpoint M of two points P(x1, y1) and Q(x2, y2) in the Cartesian plane is given by M = [(x1 + x2) / 2 , (y1 + y2) / 2].
Graphing Relations and Functions
Relations and functions can be graphed in the Cartesian plane. A relation is a set of ordered pairs, and a function is a special kind of relation where each x-coordinate is paired with exactly one y-coordinate.
Frequently Asked Questions About Cartesian Coordinate Planes
Who Invented the Coordinate Plane?
The coordinate plane, also known as Cartesian plane, was invented by the French mathematician Rene Descartes in the 17th century.
Do the x-axis and y-axis intersect perpendicular to each other in the cartesian plane?
Yes, the x-axis and y-axis intersect each other at a right angle (90 degrees) at the origin in the Cartesian plane.
What is an XY Coordinate?
An XY coordinate is an ordered pair of numbers (x, y) that represents the location of a point on the Cartesian plane.
How Many Quadrants are there in a Coordinate Plane?
There are four quadrants in a Coordinate Plane. They are labelled as Quadrant I, Quadrant II, Quadrant III and Quadrant IV.
What are the Types Of Lines in a Coordinate Plane?
There are several types of lines that can be drawn in the coordinate plane, including horizontal lines, vertical lines, diagonal lines, and curved lines.
Solved Examples on Coordinate Plane
Let’s take a look at some examples of how to plot points and find coordinates in the coordinate plane.
Example 1: Plot the point P(2,3)
- Start at the origin (0,0)
- Move 2 units to the right on the x-axis
- From that point, move 3 units up parallel to the y-axis
- Mark the point P
Example 2: Find the coordinates of the point Q
The point Q is located 3 units to the left of the origin on the x-axis and 4 units down from the origin on the y-axis. Therefore, the coordinates of Q are (-3,-4).
Example 3: Find the midpoint of the line segment joining the points A(1,2) and B(3,4)
The midpoint is given by the formula [(x1+x2)/2, (y1+y2)/2]. Substituting the given coordinates, we get [(1+3)/2, (2+4)/2] = [2,3]. Therefore, the midpoint is M(2,3).
How Kunduz Can Help You Learn Coordinate Planes?
Kunduz is an online educational platform that provides a wealth of resources to help students understand and master concepts like the coordinate plane. It offers personalized tutoring, interactive learning tools, and a vast library of educational content. With Kunduz, learning coordinate planes becomes easy, enjoyable, and effective.
