In mathematics, the centroid of a triangle is a significant point that lies within the triangle. It is the point of intersection of the three medians of the triangle. A median of a triangle is a line segment that connects a vertex of the triangle to the midpoint of the opposite side. The medians of a triangle are concurrent, meaning they all intersect at a single point, known as the centroid.
The centroid is a crucial concept in geometry, as it helps us understand the balance and stability of a triangle. It is often referred to as the center of gravity of the triangle, as it represents the point where the triangle would balance perfectly if it were made of a uniform material.
What is Centroid?
The centroid is a point that lies within a triangle and is defined as the point of intersection of the three medians of the triangle. Each median divides the triangle into two smaller triangles of equal area, and the centroid is the point where the medians intersect.
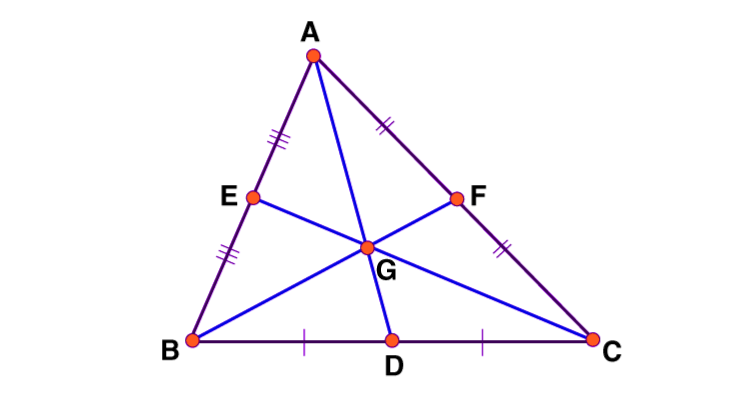
What is the Centroid of a Triangle?
The centroid of a triangle is the point of concurrency of its three medians. It is the point where the medians intersect. The medians of a triangle are the line segments that connect each vertex to the midpoint of the opposite side. The centroid is also known as the center of gravity of the triangle.
The centroid of a triangle is always located inside the triangle. It is considered one of the four points of concurrency in a triangle, along with the circumcenter, incenter, and orthocenter.
Centroid of a Triangle Formula
The formula for finding the centroid of a triangle is as follows:
Centroid of a triangle = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3)
Where x1, x2, and x3 are the x-coordinates of the vertices of the triangle, and y1, y2, and y3 are the y-coordinates of the vertices of the triangle.
Derivation of Centroid of a Triangle formula
To derive the formula for the centroid of a triangle, let’s consider a triangle ABC with vertices A(x1, y1), B(x2, y2), and C(x3, y3).
The midpoint of the side BC is D, which can be calculated using the midpoint formula as ((x2 + x3)/2, (y2 + y3)/2).
Since the centroid G divides the median in the ratio of 2:1, we can calculate the coordinates of the centroid using the section formula.
To find the x-coordinate of G: x = (2(x2 + x3)/2 + 1.x1 )/ (2+1) x = (x2 + x3 + x1)/3
To find the y-coordinate of G: y = (2(y2 + y3)/2 + 1.y1 )/ (2+1) y = (y2 + y3 + y1)/3
Therefore, the coordinates of the centroid G are ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3).
Centroid of a Triangle Theorem And Proof
The centroid of a triangle has a significant property known as the Centroid Theorem. According to the Centroid Theorem, the centroid of a triangle divides each median into two segments, with the ratio of the lengths of the two segments being 2:1.
This means that the distance from the centroid to a vertex is twice the distance from the centroid to the midpoint of the opposite side.
The Centroid Theorem can be proven using vector algebra or coordinate geometry. Let’s consider a triangle ABC with vertices A(x1, y1), B(x2, y2), and C(x3, y3).
The coordinates of the centroid G are ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3).
The length of the median AG is given by the distance formula as follows: AG = sqrt((x1 – ((x2 + x3)/2))^2 + (y1 – ((y2 + y3)/2))^2)
Similarly, we can calculate the lengths of the other medians BG and CG.
By substituting the coordinates of the centroid G and simplifying the expressions, we can show that AG:BG:CG = 2:1:1.
Hence, the Centroid Theorem is proven.
Properties of Centroid of a Triangle
The centroid of a triangle has several properties that make it a significant point in geometry. Some of the key properties of the centroid are as follows:
- The centroid is located at the intersection of the three medians of a triangle.
- The centroid divides each median into two segments, with the ratio of the lengths of the segments being 2:1.
- The centroid is always located inside the triangle.
- The centroid is one of the four points of concurrency in a triangle, along with the circumcenter, incenter, and orthocenter.
- The centroid is also known as the center of gravity of the triangle, as it represents the point where the triangle would balance perfectly if it were made of a uniform material.
- The centroid is equidistant from the three vertices of the triangle.
- The centroid is the point of minimum total distance to all the points on the triangle.
- The centroid is the arithmetic mean of the coordinates of the vertices of the triangle.
These properties of the centroid make it a useful tool in various mathematical and geometric applications.
How to Find the Centroid of a Triangle with Coordinates of Vertices
To find the centroid of a triangle when the coordinates of its vertices are known, we can use the centroid formula.
Let’s consider a triangle with vertices A(x1, y1), B(x2, y2), and C(x3, y3).
The coordinates of the centroid G can be calculated using the formula: G(x, y) = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3)
By substituting the values of x1, x2, x3, y1, y2, and y3 into the formula, we can find the coordinates of the centroid G.
For example, if the coordinates of the vertices of a triangle are A(1, 2), B(3, 4), and C(5, 6), the coordinates of the centroid G can be calculated as follows: G(x, y) = ((1 + 3 + 5)/3, (2 + 4 + 6)/3) G(x, y) = (9/3, 12/3) G(x, y) = (3, 4)
Therefore, the centroid of the triangle with vertices A(1, 2), B(3, 4), and C(5, 6) is G(3, 4).
Centroid of a Right Triangle
In a right triangle, the centroid is located at one-third the distance from the right angle vertex to the midpoint of the hypotenuse.
Consider a right triangle ABC, where C is the right angle vertex. The midpoint of the hypotenuse AB is D.
The coordinates of the centroid G can be calculated using the formula: G(x, y) = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3)
In the case of a right triangle, the centroid is located at (x, y) = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3) = (x1/3, y1/3) = (x1/3, y1/3), where (x1, y1) are the coordinates of the right angle vertex C.
Therefore, the centroid of a right triangle is located at one-third the distance from the right angle vertex to the midpoint of the hypotenuse.

Centroid and Orthocenter of a Triangle
The centroid and the orthocenter are two important points associated with a triangle. The centroid is the point of intersection of the three medians of a triangle, while the orthocenter is the point of intersection of the three altitudes of a triangle.
The altitudes of a triangle are the perpendiculars drawn from each vertex of the triangle to the opposite side.
The centroid and the orthocenter have some interesting properties and relationships:
- The centroid is always located inside the triangle, while the orthocenter can be located inside, outside, or on the triangle depending on the type of triangle.
- The centroid divides each median into two segments, with the ratio of the lengths of the segments being 2:1. On the other hand, the orthocenter does not divide the altitudes into any particular ratio.
- The centroid is considered the center of gravity of the triangle, while the orthocenter is not directly related to the concept of mass or balance.
- The centroid and the orthocenter are not always the same point, except in the case of an equilateral triangle.
In summary, the centroid and the orthocenter are two distinct points associated with a triangle, each with its own unique properties and characteristics.
| Centroid | Orthocenter |
|---|---|
| Located inside the triangle | Located inside, outside, or on the triangle |
| Divides each median into two segments in a 2:1 ratio | Does not divide the altitudes into any particular ratio |
| Considered the center of gravity of the triangle | Not directly related to the concept of mass or balance |
| Not always the same point as the orthocenter, except in the case of an equilateral triangle | Not always the same point as the centroid |
Centroid and Incenter of a Triangle
The centroid and the incenter are two important points associated with a triangle. The centroid is the point of intersection of the three medians of a triangle, while the incenter is the point of intersection of the angle bisectors of the three interior angles of a triangle.
The angle bisectors of a triangle are the lines that divide each interior angle into two equal angles.
The centroid and the incenter have some interesting properties and relationships:
- The centroid is always located inside the triangle, while the incenter is always located inside the triangle.
- The centroid divides each median into two segments, with the ratio of the lengths of the segments being 2:1. On the other hand, the incenter divides each angle bisector into two segments, with the ratio of the lengths of the segments being proportional to the lengths of the adjacent sides.
- The centroid is considered the center of gravity of the triangle, while the incenter is considered the center of the inscribed circle of the triangle.
- The centroid and the incenter are not always the same point, except in the case of an equilateral triangle.
In summary, the centroid and the incenter are two distinct points associated with a triangle, each with its own unique properties and characteristics.
| Centroid | Incenter |
|---|---|
| Located inside the triangle | Located inside the triangle |
| Divides each median into two segments in a 2:1 ratio | Divides each angle bisector into segments proportional to the lengths of the adjacent sides |
| Considered the center of gravity of the triangle | Considered the center of the inscribed circle of the triangle |
| Not always the same point as the incenter, except in the case of an equilateral triangle | Not always the same point as the centroid |
Difference Between a Median and Centroid of a Triangle
In geometry, a median is a line segment that connects a vertex of a triangle to the midpoint of the opposite side. On the other hand, the centroid is the point of intersection of the three medians of a triangle.
Here are the key differences between a median and the centroid of a triangle:
- Definition: A median is a line segment that connects a vertex of a triangle to the midpoint of the opposite side. The centroid is the point of intersection of the three medians of a triangle.
- Location: A median is a line segment, while the centroid is a point.
- Number: A triangle has three medians, one from each vertex. The centroid is a single point where all three medians intersect.
- Purpose: The medians of a triangle divide the triangle into smaller triangles of equal area. The centroid represents the balancing point or center of gravity of the triangle.
- Ratios: The centroid divides each median into two segments, with the ratio of the lengths of the segments being 2:1. The median is not divided into any specific ratio.
- Location within the triangle: The medians of a triangle always intersect within the triangle, while the centroid is always located within the triangle.
In summary, a median is a line segment that connects a vertex to the midpoint of the opposite side, while the centroid is the point where all three medians intersect.
| Median of a Triangle | Centroid of a Triangle |
|---|---|
| Line segment | Point |
| Three medians, one from each vertex | Single point of intersection of the three medians |
| Divides the triangle into smaller triangles of equal area | Represents the balancing point or center of gravity of the triangle |
| No specific ratio | Divides each median into two segments in a 2:1 ratio |
| Always intersects within the triangle | Always located within the triangle |
How do You Find the Centroid?
To find the centroid of a triangle, follow these steps:
- Identify the coordinates of the vertices of the triangle. Let’s say the coordinates are A(x1, y1), B(x2, y2), and C(x3, y3).
- Use the centroid formula to calculate the coordinates of the centroid.
- The x-coordinate of the centroid is (x1 + x2 + x3)/3.
- The y-coordinate of the centroid is (y1 + y2 + y3)/3.
- Substitute the values of x1, x2, x3, y1, y2, and y3 into the centroid formula to find the coordinates of the centroid.
- The resulting coordinates represent the location of the centroid within the triangle.
By following these steps, you can easily find the centroid of any given triangle.
Solved Examples on Centroid
Let’s solve some examples to understand how to find the centroid of a triangle.
Example 1: Find the centroid of a triangle with vertices A(1, 2), B(3, 4), and C(5, 6).
Solution: Using the centroid formula, we can calculate the coordinates of the centroid as follows: x-coordinate of the centroid = (1 + 3 + 5)/3 = 9/3 = 3 y-coordinate of the centroid = (2 + 4 + 6)/3 = 12/3 = 4
Therefore, the centroid of the triangle with vertices A(1, 2), B(3, 4), and C(5, 6) is G(3, 4).
Example 2: Determine the coordinates of the centroid of a triangle whose vertices are (-1, -3), (2, 1), and (8, -4).
Solution: Given the vertices coordinates as (-1, -3), (2, 1), and (8, -4), we can use the centroid formula to find the coordinates of the centroid.
x-coordinate of the centroid = (-1 + 2 + 8)/3 = 9/3 = 3 y-coordinate of the centroid = (-3 + 1 – 4)/3 = -6/3 = -2
Therefore, the centroid of the triangle with vertices (-1, -3), (2, 1), and (8, -4) is G(3, -2).
Example 3: Find the centroid of a right triangle with vertices A(0, 0), B(0, 3), and C(4, 0).
Solution: In a right triangle, the centroid is located at one-third the distance from the right angle vertex to the midpoint of the hypotenuse.
The coordinates of the right angle vertex C are (4, 0). The coordinates of the midpoint of the hypotenuse AB can be calculated as follows: Midpoint of AB = ((x1 + x2)/2, (y1 + y2)/2) = ((0 + 0)/2, (0 + 3)/2) = (0, 1.5)
The coordinates of the centroid G can be calculated as follows: x-coordinate of the centroid = (1/3)(4) = 4/3 y-coordinate of the centroid = (1/3)(1.5) = 0.5
Therefore, the centroid of the right triangle with vertices A(0, 0), B(0, 3), and C(4, 0) is G(4/3, 0.5).
These examples demonstrate how to find the centroid of a triangle using the centroid formula and the coordinates of the vertices.
How Kunduz Can Help You Learn Centroid?
Kunduz is an online learning platform that offers comprehensive resources and expert guidance to help you learn about the centroid of a triangle. With Kunduz, you can access a wide range of educational materials, including video tutorials, practice problems, and interactive quizzes, to enhance your understanding of this geometric concept.
Our expert tutors are available to provide personalized assistance and answer any questions you may have about the centroid of a triangle. Whether you’re a beginner or an advanced learner, Kunduz offers a supportive and engaging learning environment to help you master this topic.
