The circumference of a circle, also known as the perimeter of a circle, is a fundamental concept in geometry. It refers to the total length of the boundary of a circle. Understanding the circumference of a circle is essential for various applications, including calculating the area of a circle or determining the amount of material needed to enclose a circular object.
An Introduction to the Circumference (Perimeter) of a Circle
In mathematics, a circle is a shape consisting of all points in a plane that are equidistant from a fixed center point. The circumference of a circle represents the distance around the outer boundary of the circle. It is commonly referred to as the perimeter of a circle.
What is the Circumference (Perimeter) of a Circle?
The circumference of a circle is the length of the complete arc that forms the boundary of the circle. It is the distance traveled when moving around the circle’s edge. The circumference is a linear measurement and is typically expressed in units such as centimeters, meters, or inches.
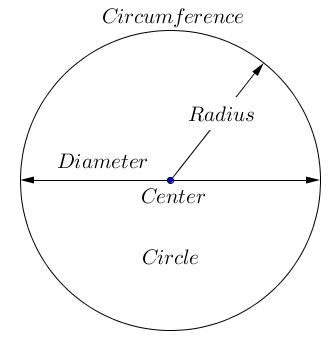
What is Circumference of a Circle?
The circumference of a circle is a measure of its boundary. If we were to cut open a circle and straighten it out, the length of the resulting line would represent the circumference of the circle. The circumference is proportional to the diameter of the circle, with the constant of proportionality being the mathematical constant π (pi).
Circumference Formula
The formula for calculating the circumference of a circle is given by:
C = 2πr
Where:
- C represents the circumference of the circle
- π (pi) is a mathematical constant approximately equal to 3.14159
- r is the radius of the circle
Alternatively, the circumference can be calculated using the diameter of the circle:
C = πd
Where:
- d represents the diameter of the circle
How To Find Circumference (Perimeter) of a Circle?
There are several methods to find the circumference of a circle, depending on the information provided. The most common methods involve using either the diameter or the radius of the circle.
How To Calculate the Circumference Using the Diameter
If the diameter of the circle is known, the circumference can be found using the formula C = πd. Simply multiply the diameter by π to obtain the circumference.
How To Calculate the Circumference Using the Radius
Alternatively, if the radius of the circle is known, the circumference can be found using the formula C = 2πr. Multiply the radius by 2π to calculate the circumference.
How To Calculate the Circumference Using the Midpoint
In some cases, the midpoint of the circle is provided instead of the radius or diameter. To find the circumference using the midpoint, the length of the circle’s radius or diameter needs to be determined first. Once the radius or diameter is known, the circumference can be calculated using the respective formulas mentioned earlier.
General Properties of Circle
A circle has several important properties that are relevant to its circumference:
- Diameter: The diameter of a circle is a straight line that passes through the center of the circle and touches two points on the circumference. It is equal to twice the length of the radius.
- Radius: The radius of a circle is the distance from the center of the circle to any point on its circumference. It is half the length of the diameter.
- Circumference to Diameter Ratio: The ratio of the circumference of a circle to its diameter is constant and approximately equal to the mathematical constant π (pi). This ratio remains the same regardless of the size of the circle.
Circumference (Perimeter) of a Circle Graph
A circle can be represented graphically, with the circumference acting as the boundary of the circle. This graph visually demonstrates the relationship between the circumference, diameter, and radius of the circle.

Area of a Circle Formula
The circumference of a circle is closely related to its area. The formula for calculating the area of a circle is given by:
A = πr^2
Where:
- A represents the area of the circle
- π (pi) is a mathematical constant approximately equal to 3.14159
- r is the radius of the circle
Perimeter of Semi-Circle
A semi-circle is half of a circle. The perimeter of a semi-circle is calculated by finding the sum of half the circumference of the full circle and the diameter of the semi-circle. The formula for the perimeter of a semi-circle is given by:
Perimeter = πr + d
Where:
- Perimeter represents the perimeter of the semi-circle
- π (pi) is a mathematical constant approximately equal to 3.14159
- r is the radius of the semi-circle
- d is the diameter of the semi-circle
Area of Semi-Circle
The area of a semi-circle is half of the area of the full circle. The formula for calculating the area of a semi-circle is given by:
Area = (πr^2)/2
Where:
- Area represents the area of the semi-circle
- π (pi) is a mathematical constant approximately equal to 3.14159
- r is the radius of the semi-circle
Radius of a Circle
The radius of a circle is the distance from the center of the circle to any point on its circumference. It is half the length of the diameter. The radius is an important parameter in calculating the circumference, area, and other properties of a circle.
.png)
Circumference to Diameter
The circumference of a circle is directly related to its diameter. The ratio of the circumference to the diameter of any circle is a constant value, which is approximately equal to the mathematical constant π (pi). This relationship is expressed by the formula:
C/D = π
Where:
- C represents the circumference of the circle
- D represents the diameter of the circle
Solved Examples on Circumference (Perimeter) of a Circle
Example 1: Given the diameter of a circle is 10 cm, find its circumference.
Solution: The circumference can be found using the formula C = πd, where d is the diameter of the circle. Substituting the given value, we have: C = π * 10 cm = 31.4 cm
Example 2: If the radius of a circle is 5 inches, what is its circumference?
Solution: The circumference can be found using the formula C = 2πr, where r is the radius of the circle. Substituting the given value, we have: C = 2π * 5 inches = 10π inches = 31.4 inches (approximately)
Example 3: Find the circumference of a circle with an area of 36π square centimeters.
Solution: The area of a circle is given by the formula A = πr^2, where r is the radius of the circle. Rearranging the formula to solve for the radius, we have: r = √(A/π) = √(36π/π) = √36 = 6 cm
Now, we can find the circumference using the formula C = 2πr: C = 2π * 6 cm = 12π cm = 37.7 cm (approximately)
How Kunduz Can Help You Learn the Circumference (Perimeter) of a Circle?
At Kunduz, we understand the importance of mastering mathematical concepts like the circumference of a circle. Our team of experienced tutors is dedicated to providing personalized and engaging learning experiences to help students excel in their math studies. Whether you need assistance with understanding the formulas, solving practice problems, or exploring real-world applications, Kunduz is here to support you every step of the way. With our intuitive online platform, you can access resources, practice exercises, and expert guidance at your convenience. Join Kunduz today and embark on a journey of mathematical success!
