In geometry, congruence is a fundamental concept that deals with the equality of two geometric figures in terms of their shape and size. When two triangles are congruent, it means that they have the exact same shape and size. This concept is crucial in various geometric proofs and problem-solving.
Congruence of triangles is determined by comparing their corresponding sides and angles. If all three sides and three angles of one triangle are congruent to the corresponding sides and angles of another triangle, then the two triangles are said to be congruent. This concept allows us to establish relationships between different parts of triangles and make accurate geometric conclusions.
What is Congruence of Triangles?
Congruence of triangles refers to the equality of corresponding sides and angles of two triangles. When two triangles are congruent, it means that every side of one triangle is equal in length to the corresponding side of the other triangle, and every angle of one triangle is equal in measure to the corresponding angle of the other triangle.
To denote congruence, the symbol “≅” is used. For example, if triangle ABC is congruent to triangle DEF, it is written as △ABC ≅ △DEF. This symbol represents the equality of corresponding parts in the congruent triangles.
Congruent Triangles
Congruent triangles have the same shape and size, meaning that their corresponding sides and angles are equal. When two triangles are congruent, they can be superimposed on each other, with all parts matching perfectly. This property allows us to manipulate and compare triangles in various geometric proofs and constructions.
For two triangles to be congruent, all three sides and three angles of one triangle must be equal to the corresponding sides and angles of the other triangle. This concept is based on the idea that if all corresponding parts of two triangles are equal, then the triangles themselves are congruent.
Symbol of Congruence
Congruence in geometry is represented by the symbol “≅”. This symbol is used to indicate that two geometric figures, such as triangles, are congruent. When two triangles are congruent, it means that all corresponding sides and angles are equal.
For example, if triangle ABC is congruent to triangle DEF, it is written as △ABC ≅ △DEF. The symbol “≅” is placed between the two triangles to indicate their congruence.
Conditions of Congruence in Triangles (How to Prove Triangles Are Congruent?)
There are several conditions or criteria that can be used to prove the congruence of triangles. These criteria are based on the equality of corresponding sides and angles. The most commonly used criteria for proving triangle congruence are:
SSS (Side-Side-Side) Criterion for Congruence
The SSS criterion states that if three sides of one triangle are equal in length to the corresponding three sides of another triangle, then the two triangles are congruent.
For example, if triangle ABC has sides AB, BC, and AC, and triangle DEF has sides DE, EF, and DF, and if AB = DE, BC = EF, and AC = DF, then △ABC ≅ △DEF.

SAS (Side-Angle-Side) Criterion for Congruence
The SAS criterion states that if two sides and the included angle of one triangle are equal in length and measure, respectively, to the corresponding two sides and included angle of another triangle, then the two triangles are congruent.
For example, if triangle ABC has sides AB, BC, and angle ∠B, and triangle DEF has sides DE, EF, and angle ∠E, and if AB = DE, BC = EF, and ∠B = ∠E, then △ABC ≅ △DEF.

ASA (Angle-Side-Angle) Criterion for Congruence
The ASA criterion states that if two angles and the included side of one triangle are equal in measure and length, respectively, to the corresponding two angles and included side of another triangle, then the two triangles are congruent.
For example, if triangle ABC has angles ∠A, ∠B, and side BC, and triangle DEF has angles ∠D, ∠E, and side EF, and if ∠A = ∠D, ∠B = ∠E, and BC = EF, then △ABC ≅ △DEF.

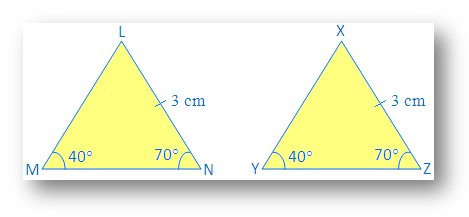
AAS (Angle-Angle-Side) Criterion for Congruence
The AAS criterion states that if two angles and a non-included side of one triangle are equal in measure to the corresponding two angles and non-included side of another triangle, then the two triangles are congruent.
For example, if triangle ABC has angles ∠A, ∠B, and side AC, and triangle DEF has angles ∠D, ∠E, and side DF, and if ∠A = ∠D, ∠B = ∠E, and AC = DF, then △ABC ≅ △DEF.
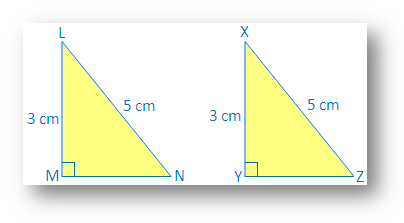
RHS (Right angle-Hypotenuse-Side) Criterion for Congruence
The RHS criterion, also known as the HL (Hypotenuse-Leg) criterion, states that if the hypotenuse and one leg of a right-angled triangle are equal in length to the corresponding hypotenuse and leg of another right-angled triangle, then the two triangles are congruent.
For example, if triangle ABC and triangle DEF are right-angled triangles, and if AC = DF and BC = EF, then △ABC ≅ △DEF.
Properties of Congruence of Triangles
Congruent triangles possess several properties that can be used in geometric proofs and constructions. These properties arise from the equality of corresponding sides and angles. Some of the key properties of congruent triangles are:
Reflexive Property
The reflexive property states that any triangle is congruent to itself. In other words, all three sides and three angles of a triangle are equal to themselves.
Symmetric Property
The symmetric property states that if triangle ABC is congruent to triangle DEF, then triangle DEF is also congruent to triangle ABC. This property allows us to reverse the order of congruence
Transitive Property
The transitive property states that if triangle ABC is congruent to triangle DEF, and triangle DEF is congruent to triangle XYZ, then triangle ABC is congruent to triangle XYZ. This property allows us to establish congruence relationships between multiple triangles.
These properties of congruent triangles are helpful in proving geometric theorems and solving geometric problems.
Difference between Similar triangles and Congruent triangles
While similar triangles and congruent triangles may seem similar, there are key differences between them. Similar triangles have the same shape but not necessarily the same size. Their corresponding angles are equal, but their corresponding sides may be proportional.
On the other hand, congruent triangles have both the same shape and size. All corresponding sides and angles of congruent triangles are equal. If two triangles are congruent, they can be superimposed on each other.
It’s important to note that two triangles with equal corresponding angles may not be congruent if their corresponding sides are not equal. This distinction is one of the fundamental principles in geometry.
CPCTC Rule
CPCTC stands for “Corresponding Parts of Congruent Triangles are Congruent.” This rule states that when two triangles are congruent, their corresponding parts, such as sides and angles, are also congruent.
For example, if triangle ABC is congruent to triangle DEF, then side AB is congruent to side DE, angle ∠A is congruent to angle ∠D, and so on. This rule allows us to make conclusions about the equality of corresponding parts in congruent triangles.
The CPCTC rule is an essential tool in geometric proofs, as it helps establish relationships between different parts of congruent triangles.
Solved Examples on Congruence of Triangles
Let’s work through some examples to apply the concepts of congruence of triangles.
Example 1: Determine whether the triangles listed below are congruent or not, and identify the criterion test for triangle congruence.
Solution:
In the above triangle, we have:
AB = DE = 7 in …side BC = EF = 4 in …side AC = DF = 5 in …side
Hence, we can say that ΔABC ≅ ΔDEF by the SSS congruence criteria.
Example 2: Determine whether the triangles listed below are congruent or not, and identify the criterion test for triangle congruence.
Solution:
In the above triangle, we have:
∠A = ∠P … angle AB = PQ = 7 units …included side ∠B = ∠Q … angle
Now, we can say that ΔABC ≅ ΔPQR by the ASA congruence criteria.
Example 3: Determine whether the triangles listed below are congruent or not, and identify the criterion test for triangle congruence.
Solution:
In the above triangle, we have:
∠A = ∠P ∠B = ∠Q BC = QR
Now, we can say that ΔABC ≅ ΔPQR by the AAS congruence criteria.
How Kunduz Can Help You Learn Congruence of Triangles?
At Kunduz, we understand the importance of mastering concepts like the congruence of triangles. Our dedicated team of experienced geometry teachers is here to guide you through the intricacies of this topic.
Through our comprehensive online courses and personalized tutoring sessions, we provide step-by-step explanations and practice problems to help you understand and apply the different criteria for proving triangle congruence. Our interactive learning materials, including videos and worksheets, ensure an engaging and effective learning experience.
With Kunduz, you can learn at your own pace, ask questions, and receive immediate feedback. Our experienced teachers are committed to helping you excel in geometry and achieve your academic goals.
