In the realm of geometry, angles play a fundamental role in understanding the relationships between lines and shapes. One important concept in geometry is that of congruent angles. Congruent angles are angles that have exactly the same measure, meaning they are identical in terms of degrees or radians. Despite their orientation or position, congruent angles maintain the same angle measurement. In this article, we will explore the definition, properties, and examples of congruent angles, as well as the criteria for determining their congruence.
What are Congruent Angles?
Congruent angles are angles that have equal measures. In other words, if two angles have the same number of degrees or radians, they are considered congruent. The term “congruent” comes from the Latin word “congruere,” which means “to agree.” When two angles are congruent, they essentially “agree” with each other in terms of their measurement. It is important to note that congruence is not affected by the direction or length of the angles. As long as the angles have the same measure, they are congruent.
How To Find Congruent Angles
To determine if two angles are congruent, we can measure their angle measurements using a protractor. By comparing the measurements, we can determine if they are equal. If the measurements are the same, the angles are congruent. It is important to note that congruent angles can be acute angles (less than 90 degrees), obtuse angles (greater than 90 degrees), exterior angles, or interior angles. The type of angle does not affect their congruence; what matters is that they have the same measure.
Congruent Angles Symbol
In mathematics, the symbol used to represent congruence is “≅”. When we want to indicate that angle A is congruent to angle B, we write it as ∠A ≅ ∠B. The symbol ≅ signifies that the two angles have the same measure and are therefore congruent.
How To Find the Measure of Congruent Angles
To find the measure of congruent angles, we can use a protractor to measure the angle. By aligning the protractor with the angle’s vertex and one of its rays, we can determine the angle’s measure. If we have two angles that are congruent, we can measure one of them and know that the other angle will have the same measure. This is because congruent angles have identical measures.
Properties of Congruent Angles
Congruent angles possess several properties that are useful in understanding their relationships. Some important properties of congruent angles include:
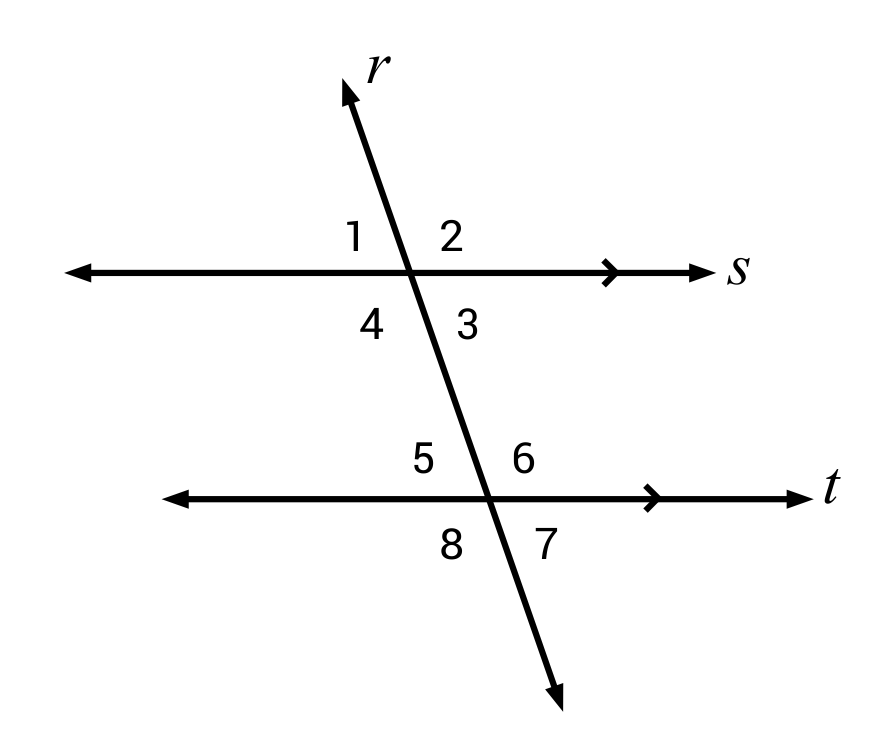
- Vertical Angles: Vertical angles, which are formed by the intersection of two lines, are always congruent. Vertical angles are opposite each other and share the same vertex.
- Corresponding Angles: When a transversal intersects two parallel lines, the corresponding angles formed are congruent. Corresponding angles are in the same relative position in relation to the parallel lines.
- Alternate Interior Angles: When a transversal intersects two parallel lines, the alternate interior angles are congruent. Alternate interior angles are located on opposite sides of the transversal and inside the two parallel lines.
- Alternate Exterior Angles: When a transversal intersects two parallel lines, the alternate exterior angles are congruent. Alternate exterior angles are located on opposite sides of the transversal and outside the two parallel lines.
These properties of congruent angles allow us determine their congruence based on their position and relationship to other angles and lines.

Corresponding Parts of Congruent Triangles
Congruent angles are often found within congruent triangles. When two triangles are congruent, it means that their corresponding parts, including angles and sides, are equal. This means that if two triangles have congruent angles, they also have congruent sides, and vice versa. Congruent triangles have the same shape and size, and their corresponding parts can be matched up perfectly.
Congruence Criteria for Triangles
There are several criteria that can be used to determine the congruence of triangles. These criteria specify the minimum conditions that two or more triangles must meet in order to be considered congruent. The main congruence criteria for triangles are:
- SSS (Side, Side, Side) Criterion: If the three sides of one triangle are congruent to the corresponding sides of another triangle, then the triangles are congruent.
- SAS (Side, Angle, Side) Criterion: If two sides and the included angle of one triangle are congruent to the corresponding sides and included angle of another triangle, then the triangles are congruent.
- ASA (Angle, Side, Angle) Criterion: If two angles and the included side of one triangle are congruent to the corresponding angles and included side of another triangle, then the triangles are congruent.
- SSA (Side, Side, Angle) Criterion: If two sides and a non-included angle of one triangle are congruent to the corresponding sides and non-included angle of another triangle, then the triangles may or may not be congruent. This criterion is sometimes referred to as the ambiguous case and requires additional information to determine congruence.
- RHS (Right angle-Hypotenuse-Side) Criterion: If the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the triangles are congruent.
These congruence criteria provide a set of conditions that can be used to determine if two triangles are congruent based on the congruence of their sides and angles.
What Type of Angles are Congruent?
Congruent angles can be found in various geometric configurations. Some types of angles that are congruent include:
- Vertical Angles: Vertical angles are formed when two lines intersect. The angles that are opposite each other, or across from each other, are congruent.
- Alternate Angles: When a transversal intersects two parallel lines, the alternate angles formed are congruent. Alternate angles are located on opposite sides of the transversal and on the interior of the two parallel lines.
- Isosceles Triangles: In an isosceles triangle, two of the angles are congruent. An isosceles triangle has two sides of equal length, which creates congruent base angles.
- Equilateral Triangles: In an equilateral triangle, all three angles are congruent. An equilateral triangle has three sides of equal length, which creates congruent angles.
- Squares and Rectangles: In squares and rectangles, all four interior angles are congruent and measure 90 degrees.
These are just a few examples of the types of angles that can be congruent. Congruent angles can be found in various geometric shapes and configurations.
Congruent Angles Theorem and Proof
There are several theorems in geometry that relate to congruent angles and provide a basis for proving their congruence. Some important congruent angles theorems include:
- Vertical Angles Theorem: The Vertical Angles Theorem states that vertical angles, which are formed by the intersection of two lines, are always congruent. This theorem can be proven by using the properties of parallel lines and alternate interior angles.
- Corresponding Angles Theorem: The Corresponding Angles Theorem states that when a transversal intersects two parallel lines, the corresponding angles formed are congruent. This theorem can be proven by using the properties of parallel lines and alternate interior angles.
- Converse of the Corresponding Angles Theorem: The Converse of the Corresponding Angles Theorem states that if the corresponding angles formed by a transversal intersecting two lines are congruent, then the lines are parallel. This theorem can be proven by using the properties of parallel lines and alternate interior angles.
- Alternate Interior Angles Theorem: The Alternate Interior Angles Theorem states that when a transversal intersects two parallel lines, the alternate interior angles formed are congruent. This theorem can be proven by using the properties of parallel lines and alternate interior angles.
- Converse of the Alternate Interior Angles Theorem: The Converse of the Alternate Interior Angles Theorem states that if the alternate interior angles formed by a transversal intersecting two lines are congruent, then the lines are parallel. This theorem can be proven by using the properties of parallel lines and alternate interior angles.
- Alternate Exterior Angles Theorem: The Alternate Exterior Angles Theorem states that when a transversal intersects two parallel lines, the alternate exterior angles formed are congruent. This theorem can be proven by using the properties of parallel lines and alternate exterior angles.
- Converse of the Alternate Exterior Angles Theorem: The Converse of the Alternate Exterior Angles Theorem states that if the alternate exterior angles formed by a transversal intersecting two lines are congruent, then the lines are parallel. This theorem can be proven by using the properties of parallel lines and alternate exterior angles.
- Overlapping Angle Theorem: The Overlapping Angle Theorem states that if two angles adjacent to a common angle are congruent, then the overlapping angles formed are congruent. This theorem can be proven by using the properties of adjacent angles and vertical angles.
- Congruent Supplements Theorem: The Congruent Supplements Theorem states that if two angles are supplements of the same angle, then the two angles are congruent. This theorem can be proven by using the properties of supplementary angles.
- Congruent Complements Theorem: The Congruent Complements Theorem states that if two angles are complements of the same angle, then the two angles are congruent. This theorem can be proven by using the properties of complementary angles.
These congruent angles theorems provide a foundation for proving the congruence of angles in various geometric configurations.
Constructing Congruent Angles
Constructing congruent angles can be a useful skill in geometry. There are different methods for constructing congruent angles, depending on the given information. Here are two common methods for constructing congruent angles:
- Construction of Two Congruent Angles: To construct two congruent angles, we can use a compass and a straight edge. The steps for this construction are as follows:
- Draw two lines of any suitable length.
- Take an arc on the compass, less than the length of the lines, and place the compass tip at the endpoint of one line. Draw an arc without changing the width of the compass.
- Repeat the previous step with the same arc, placing the compass tip at the endpoint of the other line.
- Draw lines that connect the two arcs, creating two congruent angles.
- Construction of a Congruent Angle to the Given Angle: To construct a congruent angle to a given angle, we can use a compass and a straight edge. The steps for this construction are as follows:
- Draw a line of any suitable length and label it.
- Place the compass tip at the vertex of the given angle and draw an arc, keeping the compass width the same.
- Repeat the previous step, placing the compass tip at a point on the line.
- Connect the vertex of the new angle to the intersection of the two arcs, creating a congruent angle to the given angle.
These construction methods allow us to create congruent angles based on the given information and the properties of angles.
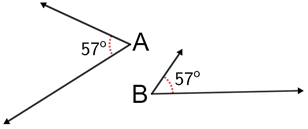
Facts About Congruent Angles
Here are some important facts about congruent angles:
- Congruent angles have the same measure in degrees or radians.
- The symbol ≅ is used to represent congruence.
- Congruent angles can be found in various geometric configurations, such as vertical angles, alternate angles, isosceles triangles, equilateral triangles, squares, and rectangles.
- Congruent angles have the same shape and size, regardless of their orientation or position.
- Congruent angles can be determined by measuring their angle measurements using a protractor.
- Congruent angles play a significant role in proving the congruence of triangles and other geometric figures.
- There are several theorems and criteria in geometry that relate to congruent angles and their properties.
Understanding these facts about congruent angles is essential for solving geometry problems and proving the congruence of geometric figures.
Frequently Asked Questions About Congruent Angles
Here are answers to some frequently asked questions about congruent angles:
Are Right Angles Congruent?
Yes, right angles, which measure 90 degrees, are always congruent to each other. All right angles have the same measure.
Do Congruent Angles Add up to 180?
No, congruent angles do not necessarily add up to 180 degrees. The sum of two congruent angles depends on their individual measures. However, if two angles are congruent and form a linear pair, their sum will be 180 degrees.
What are the Conditions Required for Congruent Angles?
The conditions required for angles to be congruent are that they have the same measure in degrees or radians. If two angles have the same number of degrees or radians, they are considered congruent.
What are Congruent Angles in Parallel Lines?
When a transversal intersects two parallel lines, congruent angles can be formed. These include corresponding angles, alternate angles, interior angles on the same side of the transversal, and exterior angles on the same side of the transversal.
How do we Know if Angles are Congruent?
To determine if angles are congruent, we can measure their angle measurements using a protractor. If the measurements are the same, the angles are congruent.
Are Congruent Angles Equal?
Yes, congruent angles have equal measures. If two angles are congruent, they have the same number of degrees or radians.
What Type of Angles are always Congruent?
Vertical angles, which are formed by the intersection of two lines, are always congruent. This means that the angles opposite each other are equal.
How to know if two numbers are congruent?
Two numbers are congruent if they have the same remainder when divided by a given natural number. This is denoted as a ≡ b mod (m), where a and b are the two numbers and m is the modulus.
These frequently asked questions provide clarification on common misconceptions and inquiries about congruent angles.
Solved Examples on Congruent Angles
Let’s solve some examples to further understand congruent angles:
Example 1: Identify the congruent angles in the following pairs of angles:
- Angle A measures 39 degrees and angle B measures 39 degrees.
- Angle C measures 42 degrees and angle D measures 39 degrees.
- Angle E measures 106 degrees and angle F measures 103 degrees.
- Angle G measures 19 degrees and angle H measures 21 degrees.
Solution:
- Angle A and angle B are congruent because they both measure 39 degrees.
- Angle C and angle D are not congruent because they have different measures.
- Angle E and angle F are not congruent because they have different measures.
- Angle G and angle H are not congruent because they have different measures.
Example 2: In a triangle, two of the three angles are congruent, and the third angle measures 40 degrees. What are the measures of the congruent angles?
Solution: Let’s assume the measure of each congruent angle is x. We know that the sum of the angles in a triangle is 180 degrees. Therefore, we can write the equation as follows: x + x + 40 = 180 2x + 40 = 180 2x = 180 – 40 2x = 140 x = 140/2 x = 70
Therefore, each congruent angle in the triangle measures 70 degrees.
By solving these examples, we can apply the concepts of congruent angles to solve various geometry problems.
How Kunduz Can Help You Learn Congruent Angles
At Kunduz, we understand the importance of mastering concepts like congruent angles in geometry. That’s why we offer comprehensive online resources and tutoring services to help students excel in their mathematics studies. Our experienced tutors provide personalized instruction, guiding students through the intricacies of congruent angles and related topics. Whether you need help with understanding the properties of congruent angles, proving the congruence of triangles, or constructing congruent angles, our tutors are here to assist you. With Kunduz, you can gain a solid understanding of congruent angles and build a strong foundation in geometry. Reach out to us today and let us help you achieve success in mathematics.
