In the study of trigonometry, angles play a crucial role in understanding various concepts and solving problems. One important aspect of angles is the concept of coterminal angles. Coterminal angles are angles that have the same initial side and the same terminal side. They differ in their values, but they occupy the same position in the coordinate plane. Understanding coterminal angles is essential in trigonometry as they help us solve problems and determine unknown angles.
What is the Coterminal Angle?
To understand coterminal angles, we need to first understand the standard position of an angle. In the standard position, the initial side of the angle is on the positive x-axis, and the terminal side is determined by the rotation of the angle. Coterminal angles share the same initial and terminal sides, but they may have different values.
For example, consider an angle of 45 degrees. In the standard position, the terminal side of the angle is in the first quadrant. If we rotate the angle counterclockwise by 360 degrees, the terminal side coincides with the initial side again, resulting in a coterminal angle of 405 degrees. Similarly, if we rotate the angle clockwise by 360 degrees, the terminal side coincides with the initial side again, resulting in a coterminal angle of -315 degrees.
How to Draw a Coterminal Angle?
Drawing a coterminal angle involves understanding the standard position of an angle and its rotation. Here’s a step-by-step guide to drawing a coterminal angle:
- Start with the given angle in the standard position, with its initial side on the positive x-axis.
- Determine the direction of rotation (clockwise or counterclockwise) to find the coterminal angle.
- Rotate the angle by adding or subtracting multiples of 360 degrees (or 2π radians) to the given angle.
- The terminal side of the coterminal angle will coincide with the initial side of the given angle.
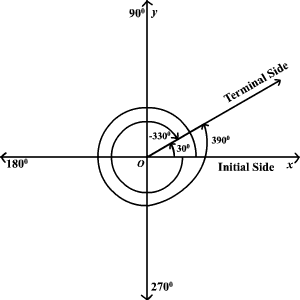
Let’s take an example to illustrate this process. Suppose we have an angle of 30 degrees. To find a coterminal angle, we can rotate the angle counterclockwise by adding multiples of 360 degrees. Let’s add 360 degrees to the given angle:
30 degrees + 360 degrees = 390 degrees
So, a coterminal angle of 30 degrees is 390 degrees.
Coterminal Angle Formula
The formula to find coterminal angles depends on whether the angle is measured in degrees or radians:
- In degrees: θ ± 360n
- In radians: θ ± 2πn
In the formula, θ represents the given angle, and n is an integer that represents the number of rotations around the coordinate plane. By adding or subtracting multiples of 360 degrees or 2π radians to the given angle, we can find coterminal angles.
Coterminal Angle Theorem
The Coterminal Angle Theorem states that two angles are coterminal if and only if the difference between their measures is a multiple of 360 degrees (or 2π radians). In other words, if the difference between two angles is a multiple of 360 degrees, they are coterminal.
This theorem is useful when determining whether two angles are coterminal or not. By calculating the difference between the measures of two angles and checking if it is a multiple of 360 degrees, we can determine if they are coterminal.
How to Find Coterminal Angles?
Finding coterminal angles involves applying the coterminal angle formula and performing calculations. Here’s a step-by-step process to find coterminal angles:
- Start with the given angle, θ.
- Determine whether the angle is measured in degrees or radians.
- If the angle is in degrees, use the formula θ ± 360n, where n is an integer.
- If the angle is in radians, use the formula θ ± 2πn, where n is an integer.
- Add or subtract multiples of 360 degrees or 2π radians to the given angle to find coterminal angles.
- Repeat the process with different values of n to find additional coterminal angles.
Let’s work through an example to demonstrate the steps. Suppose we have an angle of 60 degrees. To find coterminal angles, we can add or subtract multiples of 360 degrees. Let’s find two coterminal angles:
- For the first coterminal angle, let n = 1 (anticlockwise rotation):
- θ + 360n = 60 + 360(1) = 420 degrees
- For the second coterminal angle, let n = -1 (clockwise rotation):
- θ + 360n = 60 + 360(-1) = -300 degrees
So, the two coterminal angles of 60 degrees are 420 degrees and -300 degrees.
Positive and Negative Coterminal Angles
Coterminal angles can be positive or negative depending on the direction of rotation. When the rotation is counterclockwise, the coterminal angle is positive. Conversely, when the rotation is clockwise, the coterminal angle is negative.
For example, let’s consider the angle 30 degrees. If we rotate the angle counterclockwise, the coterminal angle will be positive. Adding multiples of 360 degrees to the given angle will result in positive coterminal angles. On the other hand, rotating the angle clockwise will result in negative coterminal angles. Subtracting multiples of 360 degrees from the given angle will yield negative coterminal angles.
Coterminal Angles and Reference Angles
Coterminal angles are closely related to reference angles. A reference angle is the acute angle formed between the terminal side of an angle and the x-axis in the standard position. The reference angle depends on the quadrant in which the terminal side lies.
To find the reference angle of an angle, we follow these steps:
- Determine the coterminal angle of the given angle that lies between 0 degrees and 360 degrees.
- Identify the quadrant in which the terminal side of the coterminal angle lies.
- Based on the quadrant, determine the reference angle using the following rules:
- First quadrant (0 to 90 degrees): The reference angle is the same as the given angle.
- Second quadrant (90 to 180 degrees): The reference angle is 180 degrees minus the given angle.
- Third quadrant (180 to 270 degrees): The reference angle is the given angle minus 180 degrees.
- Fourth quadrant (270 to 360 degrees): The reference angle is 360 degrees minus the given angle.
By finding the reference angle, we can better understand the relationship between coterminal angles and their position in the coordinate plane.
Basic Cartesian Coordinate System, Angles in Standard Position, Coterminal Angles
To fully grasp the concept of coterminal angles, we need to understand the basic Cartesian coordinate system and angles in standard position. The Cartesian coordinate system consists of two perpendicular axes, the x-axis and the y-axis, which intersect at the origin (0, 0). Angles in the coordinate plane are measured in degrees or radians and are formed by the rotation of a ray about its initial point.
Angles in standard position are angles that have their initial side on the positive x-axis and their terminal side determined by the rotation of the angle. In this position, the vertex of the angle is at the origin, and the terminal side can lie in any quadrant of the coordinate plane.
Coterminal angles, as previously mentioned, have the same initial and terminal sides. They occupy the same position in the coordinate plane, but their values differ. By adding or subtracting multiples of 360 degrees or 2π radians to a given angle, we can find coterminal angles that share the same position but have different measures.
Coterminal Angles in Degrees
When working with coterminal angles in degrees, we use the formula θ ± 360n, where θ represents the given angle and n is an integer that represents the number of rotations around the coordinate plane. By adding or subtracting multiples of 360 degrees to the given angle, we can generate coterminal angles.
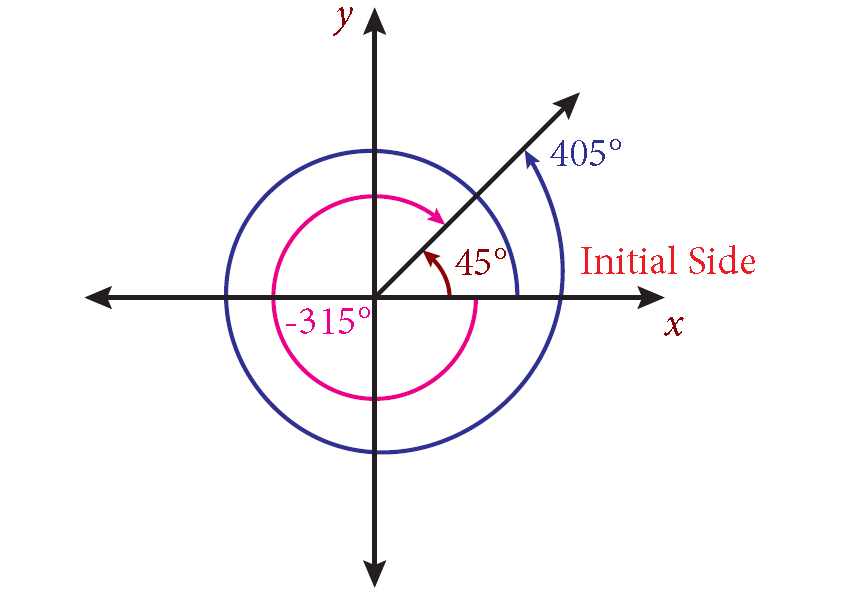
For example, let’s find coterminal angles of 45 degrees:
- For the first coterminal angle, let n = 1 (anticlockwise rotation):
- θ + 360n = 45 + 360(1) = 405 degrees
- For the second coterminal angle, let n = -1 (clockwise rotation):
- θ + 360n = 45 + 360(-1) = -315 degrees
So, the two coterminal angles of 45 degrees are 405 degrees and -315 degrees.
Coterminal Angles in Radians
In trigonometry, angles can also be measured in radians. To find coterminal angles in radians, we use the formula θ ± 2πn, where θ represents the given angle in radians and n is an integer that represents the number of rotations around the coordinate plane. By adding or subtracting multiples of 2π radians to the given angle, we can determine coterminal angles.
For example, let’s find coterminal angles of π/4 radians:
- For the first coterminal angle, let n = 1 (anticlockwise rotation):
- θ + 2πn = π/4 + 2π(1) = 9π/4 radians
- For the second coterminal angle, let n = -1 (clockwise rotation):
- θ + 2πn = π/4 + 2π(-1) = -7π/4 radians
So, the two coterminal angles of π/4 radians are 9π/4 and -7π/4.
Importance of Coterminal Angles in Trigonometry
Coterminal angles are important in trigonometry as they help us solve problems and determine unknown angles. By finding coterminal angles, we can simplify calculations and better understand the relationship between angles in the coordinate plane. They also allow us to work with angles that have different measures but occupy the same position, making it easier to compare and analyze trigonometric functions.
In addition, coterminal angles play a role in determining the reference angle of an angle. The reference angle is crucial in trigonometry as it helps us calculate trigonometric functions accurately and efficiently.
Properties of Coterminal Angles
Coterminal angles share several properties that are important to understand in trigonometry. These properties include:
- Difference between coterminal angles: The difference between two coterminal angles is always a multiple of 360 degrees or 2π radians. This property helps us identify and generate coterminal angles.
- Same trigonometric values: Coterminal angles have the same values for the trigonometric functions of sine, cosine, and tangent. This property allows us to simplify calculations and analyze trigonometric relationships.
- Infinite coterminal angles: The number of coterminal angles of a given angle is infinite. This is because there are an infinite number of multiples of 360 degrees or 2π radians that can be added or subtracted to the given angle to generate coterminal angles.
Understanding these properties helps us manipulate and work with coterminal angles effectively in trigonometry.
Solved Examples on Coterminal Angles
Let’s solve a few examples to further illustrate the concept of coterminal angles:
Example 1:
Find two coterminal angles of 30 degrees.
Solution:
Given angle: 30 degrees
To find the coterminal angles, we can add or subtract multiples of 360 degrees.
- For the first coterminal angle, let n = 1 (anticlockwise rotation):
- θ + 360n = 30 + 360(1) = 390 degrees
- For the second coterminal angle, let n = -2 (clockwise rotation):
- θ + 360n = 30 + 360(-2) = -690 degrees
So, the two coterminal angles of 30 degrees are 390 degrees and -690 degrees.
Example 2:
Find a coterminal angle of π/3 radians.
Solution:
Given angle: π/3 radians
To find a coterminal angle, we can add or subtract multiples of 2π radians.
- Let’s subtract 2π from the given angle:
- θ – 2π = π/3 – 2π = -5π/3 radians
So, a coterminal angle of π/3 radians is -5π/3 radians.
Example 3:
Find a positive and a negative coterminal angle of 45 degrees.
Solution:
Given angle: 45 degrees
To find a positive coterminal angle, we can rotate the angle counterclockwise by adding multiples of 360 degrees. Let’s choose n = 1:
- Positive coterminal angle:
- θ + 360n = 45 + 360(1) = 405 degrees
To find a negative coterminal angle, we can rotate the angle clockwise by subtracting multiples of 360 degrees. Let’s choose n = -1:
- Negative coterminal angle:
- θ + 360n = 45 + 360(-1) = -315 degrees
So, the positive coterminal angle of 45 degrees is 405 degrees, and the negative coterminal angle is -315 degrees.
How Kunduz Can Help You Learn Coterminal Angles?
Whether you’re a beginner or looking to improve your skills, Kunduz is here to guide you on your learning journey. Our user-friendly platform and affordable pricing make it accessible for everyone to access high-quality educational content. Join Kunduz today and unlock your potential in trigonometry!
