When it comes to describing points in a three-dimensional space, the Cartesian coordinate system is commonly used. However, there are instances where describing points on surfaces such as cylinders can be challenging using Cartesian coordinates alone. This is where cylindrical coordinates come into play. Cylindrical coordinates provide a natural extension of polar coordinates into three-dimensional space and are particularly useful in analyzing and solving problems involving cylindrical shapes.
In this article, we will explore the concept of cylindrical coordinates, understand how they relate to the Cartesian coordinate system, learn how to convert between cylindrical and rectangular coordinates, and discuss the applications and properties of cylindrical coordinates. So, let’s dive right in!
What are Cylindrical Coordinates?
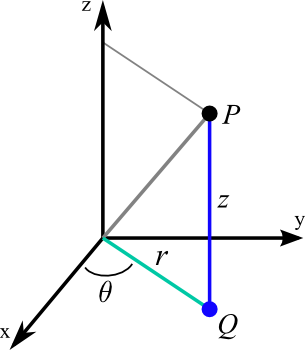
Cylindrical coordinates are a set of three coordinates, denoted as (r, θ, z), that describe the location of a point in the three-dimensional cylindrical coordinate system. These coordinates combine the polar coordinates (r, θ) in the xy-plane with the z-coordinate in the Cartesian coordinate system.
To understand cylindrical coordinates, let’s break down each component:
- r: The radial distance, denoted as r, represents the distance from the origin to the projection of the point in the xy-plane. It is similar to the polar coordinate’s radial distance.
- θ: The azimuthal angle, denoted as θ, represents the angle between the positive x-axis and the line segment connecting the origin and the point in the xy-plane. This angle is measured in radians.
- z: The z-coordinate represents the vertical height of the point above or below the xy-plane. It is the same as the z-coordinate in the Cartesian coordinate system.
Together, these three coordinates provide a complete description of a point in the cylindrical coordinate system. For example, the cylindrical coordinates (2, π/4, 3) represent a point that is located 2 units away from the origin along the radial direction, at an angle of π/4 from the positive x-axis, and 3 units above the xy-plane.

What is a Cylindrical Coordinate System?
A cylindrical coordinate system is a three-dimensional coordinate system that incorporates cylindrical coordinates to describe the position of a point in space. It is an extension of the polar coordinate system into three dimensions. In the cylindrical coordinate system, each point is represented by its radial distance, azimuthal angle, and vertical height.
The cylindrical coordinate system is particularly useful when dealing with problems involving cylindrical shapes, such as calculating the volume of a round water tank or analyzing fluid flow in a pipe. It allows us to simplify the equations and calculations involved in such problems by utilizing the inherent symmetry of the cylindrical shape.
In the cylindrical coordinate system, if we hold one coordinate constant, we can trace out various surfacs:
- If r is constant, a cylindrical surface is obtained, which is a set of points that lie at a fixed distance from the origin.
- If θ is constant, a vertical plane can be traced out, which is a set of points that lie along a line at a fixed angle from the positive x-axis.
- If z is constant, a flat circular plane is obtained, which is a set of points lying at a fixed height above or below the xy-plane.
These surfaces help us visualize and analyze various geometrical and physical phenomena in cylindrical coordinate systems.
How To Find Cylindrical Coordinates?
To find the cylindrical coordinates of a point, we need to project the point onto the xy-plane and determine its polar coordinates (r, θ) in the plane. We also need to consider the vertical height (z) of the point above or below the xy-plane.
Let’s say we have a point P in the three-dimensional space and we want to find its cylindrical coordinates. Here’s a step-by-step process to determine the cylindrical coordinates:
- Project the point P onto the xy-plane to obtain the point Q, which represents the projection of P in the xy-plane.
- Determine the polar coordinates (r, θ) of Q. The radial distance r is the distance from the origin to Q, and the azimuthal angle θ is the angle between the positive x-axis and the line segment connecting the origin and Q.
- Determine the vertical height z of the point P above or below the xy-plane.
The cylindrical coordinates of the point P are then represented as (r, θ, z). This process allows us to uniquely locate a point in the cylindrical coordinate system.
Cylindrical Coordinates Graph
To visualize the concept of cylindrical coordinates, we can plot points in the three-dimensional Cartesian coordinate system. The cylindrical coordinates (r, θ, z) correspond to a specific location in space, determined by the radial distance r, azimuthal angle θ, and vertical height z.
By plotting points with different cylindrical coordinates, we can create a graph that represents the cylindrical coordinate system. This graph allows us to visualize and analyze the positions of points in three-dimensional space.
When graphing cylindrical coordinates, the radial distance r determines how far the point is from the origin, the azimuthal angle θ determines the direction from the positive x-axis, and the vertical height z determines the position above or below the xy-plane.
By plotting multiple points and connecting them, we can visualize surfaces and objects in cylindrical coordinates, such as cylinders and curved planes. This graph helps us gain a better understanding of the spatial relationships between points and surfaces in the cylindrical coordinate system.
What is Cartesian?
Before we delve deeper into cylindrical coordinates, it’s important to have a good understanding of the Cartesian coordinate system. The Cartesian coordinate system, also known as the rectangular coordinate system, is a fundamental framework for representing points in a two-dimensional or three-dimensional space.
In the Cartesian coordinate system, each point is represented by an ordered pair (x, y) in two dimensions or an ordered triple (x, y, z) in three dimensions. The x-coordinate represents the horizontal position, the y-coordinate represents the vertical position, and the z-coordinate represents the depth or height position.
The Cartesian coordinate system provides a simple and intuitive way to describe the position of points in space. It allows for precise measurements and calculations, making it a widely used system in various fields such as mathematics, physics, and engineering.
The cylindrical coordinate system, as an extension of polar coordinates, complements the Cartesian coordinate system by providing an alternative representation for points in space, particularly when dealing with problems involving cylindrical shapes.
Cylindrical Coordinates Conversions
Converting between cylindrical and rectangular coordinates is a crucial skill when working with cylindrical coordinates. By converting between these coordinate systems, we can seamlessly transition from one representation to another, depending on the requirements of a problem or analysis.
Let’s explore the conversions between cylindrical and rectangular coordinates in detail:
Cylindrical Coordinates to Cartesian Coordinates
To convert cylindrical coordinates (r, θ, z) to Cartesian coordinates (x, y, z), we use the following formulas:
- x = r * cos(θ)
- y = r * sin(θ)
- z = z
In these formulas, x and y represent the horizontal and vertical positions in the Cartesian coordinate plane, respectively. The radial distance r and azimuthal angle θ determine the position in the xy-plane, while the z-coordinate remains the same.
Cartesian Coordinates to Cylindrical Coordinates
Conversely, we can convert Cartesian coordinates (x, y, z) to cylindrical coordinates (r, θ, z) using the following formulas:
- r = √(x² + y²)
- θ = tan^(-1)(y / x)
- z = z
In these formulas, r represents the radial distance from the origin to the projection of the point in the xy-plane, while θ represents the azimuthal angle between the positive x-axis and the line segment connecting the origin and the point. The z-coordinate remains the same.
These conversion formulas allow us to transform coordinates between the cylindrical and Cartesian systems, enabling us to work with different coordinate representations as needed.
Spherical Coordinates to Cylindrical Coordinates
Spherical coordinates offer yet another coordinate system that can be converted to cylindrical coordinates. The conversion from spherical coordinates (ρ, θ, φ) to cylindrical coordinates (r, θ, z) can be achieved using the following equations:
- r = ρ * sin(φ)
- θ = θ
- z = ρ * cos(φ)
In these equations, ρ represents the radial distance from the origin to the point, φ represents the inclination angle from the positive z-axis, and θ remains the same as the azimuthal angle in cylindrical coordinates.
By performing these conversions, we can seamlessly switch between spherical and cylindrical coordinate systems, depending on the problem at hand.
Convert from Cylindrical to Rectangular Coordinates
To convert cylindrical coordinates (r, θ, z) to rectangular coordinates (x, y, z), we use the following formulas:
- x = r * cos(θ)
- y = r * sin(θ)
- z = z
In these formulas, r represents the radial distance from the origin to the point, θ represents the azimuthal angle, and z represents the vertical height above or below the xy-plane. By substituting these values into the formulas, we can determine the corresponding rectangular coordinates.
Convert from Rectangular to Cylindrical Coordinates
Conversely, we can convert rectangular coordinates (x, y, z) to cylindrical coordinates (r, θ, z) using the following formulas:
- r = √(x² + y²)
- θ = tan^(-1)(y / x)
- z = z
In these formulas, x and y represent the horizontal and vertical positions, respectively, while z represents the vertical height. By substituting these values into the formulas, we can determine the corresponding cylindrical coordinates.
Convert from Spherical to Rectangular Coordinates
To convert spherical coordinates (ρ, θ, φ) to rectangular coordinates (x, y, z), we use the following formulas:
- x = ρ * sin(φ) * cos(θ)
- y = ρ * sin(φ) * sin(θ)
- z = ρ * cos(φ)
In these formulas, ρ represents the radial distance from the origin to the point, θ represents the azimuthal angle, and φ represents the inclination angle. By substituting these values into the formulas, we can determine the corresponding rectangular coordinates.
Convert from Rectangular to Spherical Coordinates
Conversely, we can convert rectangular coordinates (x, y, z) to spherical coordinates (ρ, θ, φ) using the following formulas:
- ρ = √(x² + y² + z²)
- θ = tan^(-1)(y / x)
- φ = cos^(-1)(z / √(x² + y² + z²))
In these formulas, x, y, and z represent the rectangular coordinates, while ρ represents the radial distance, θ represents the azimuthal angle, and φ represents the inclination angle. By substituting these values into the formulas, we can determine the corresponding spherical coordinates.
These conversions between cylindrical, rectangular, and spherical coordinates allow us to seamlessly switch between different coordinate systems, depending on the problem at hand. They provide a versatile toolkit for working with points in three-dimensional space.
Cylindrical Coordinates Integral
When working with problems involving cylindrical coordinates, such as calculating volumes or evaluating integrals, we often need to express the integral in terms of cylindrical coordinates. This allows us to simplify the problem and take advantage of the inherent symmetry of the cylindrical shape.
The volume element in cylindrical coordinates is given by:
- dV = r * dr * dθ * dz
In this equation, r represents the radial distance, dr represents an infinitesimal change in r, dθ represents an infinitesimal change in θ, and dz represents an infinitesimal change in z. Multiplying these infinitesimal changes together gives us the volume element, which we can integrate over to find the desired volume or evaluate integrals in cylindrical coordinates.
To perform integrals in cylindrical coordinates, we need to express the integrand and limits of integration in terms of r, θ, and z. Once we have done that, we can use the volume element and appropriate limits of integration to set up and evaluate the integral.
Cylindrical coordinates provide a convenient framework for solving problems involving cylindrical shapes, as well as a versatile coordinate system for evaluating integrals and finding volumes.
Cylindrical Coordinates Calculator
When working with cylindrical coordinates, it can be helpful to use a calculator or software tool to perform calculations and conversions quickly and accurately. A cylindrical coordinates calculator allows you to input the values of r, θ, and z and obtain the corresponding rectangular coordinates, or vice versa.
With a cylindrical coordinates calculator, you can perform various calculations, such as converting between cylindrical and rectangular coordinates, finding the volume of a cylindrical shape, evaluating integrals in cylindrical coordinates, and much more. These calculators help save time and ensure accuracy in your mathematical calculations.
There are several online resources and software tools available that provide cylindrical coordinates calculators. These calculators typically have user-friendly interfaces and allow you to input values and obtain results with ease. When working with cylindrical coordinates, having access to a calculator can greatly simplify your calculations and enhance your productivity.
Cylindrical Coordinates Grapher
A cylindrical coordinates grapher is a powerful tool that allows you to visualize and explore surfaces and objects in the cylindrical coordinate system. With a grapher, you can input equations or parametric equations in cylindrical coordinates and generate interactive graphs to gain insights into their shapes and properties.
A cylindrical coordinates grapher enables you to plot surfaces, curves, and points in three-dimensional space based on their cylindrical coordinates. You can manipulate the viewing angle, zoom in and out, and rotate the graph to gain a better understanding of the object’s geometry. This visualization tool is particularly useful when studying and analyzing cylindrical shapes and their characteristics.
There are various software tools and online resources available that provide cylindrical coordinates graphers. These graphers often offer additional features, such as the ability to plot multiple surfaces, apply color mapping, and overlay coordinate grids. With a cylindrical coordinates grapher, you can explore complex shapes, visualize mathematical concepts, and enhance your understanding of cylindrical coordinates.
Cylindrical Coordinates Formula
The formulas for converting between cylindrical and rectangular coordinates have been discussed earlier. To summarize, here are the formulas:
Cylindrical to Rectangular Coordinates:
- x = r * cos(θ)
- y = r * sin(θ)
- z = z
Rectangular to Cylindrical Coordinates:
- r = √(x² + y²)
- θ = tan^(-1)(y / x)
- z = z
These formulas allow us to convert coordinates between cylindrical and rectangular systems and vice versa. By using these formulas, we can seamlessly transition between different coordinate representations depending on the problem or analysis at hand.
Frequently Asked Questions About Cylindrical Coordinates
What are cylindrical coordinates?
Cylindrical coordinates are a set of three coordinates, (r, θ, z), that describe the location of a point in a three-dimensional cylindrical coordinate system. They combine the polar coordinates (r, θ) in the xy-plane with the z-coordinate in the Cartesian coordinate system.
How do you convert cylindrical coordinates to rectangular coordinates?
To convert cylindrical coordinates (r, θ, z) to rectangular coordinates (x, y, z), use the following formulas:
- x = r * cos(θ)
- y = r * sin(θ)
- z = z
How do you convert rectangular coordinates to cylindrical coordinates?
To convert rectangular coordinates (x, y, z) to cylindrical coordinates (r, θ, z), use the following formulas:
- r = √(x² + y²)
- θ = tan^(-1)(y / x)
- z = z
What are the applications of cylindrical coordinates?
Cylindrical coordinates are useful in analyzing and solving problems involving cylindrical shapes, such as calculating volumes, analyzing fluid flow in pipes, and studying electric fields in cylindrical symmetry. They provide a convenient representation for working with cylindrical systems and taking advantage of their inherent symmetry.
What is the difference between cylindrical and Cartesian coordinates?
Cylindrical coordinates provide an alternative representation for points in a three-dimensional space, particularly when dealing with cylindrical shapes. While Cartesian coordinates describe the position of a point using three distances along the x, y, and z axes, cylindrical coordinates combine polar coordinates in the xy-plane with the z-coordinate to represent points in a cylindrical coordinate system.
Solved Examples on Cylindrical Coordinates
Example 1: Convert the cylindrical coordinates (2, π/4, 3) to rectangular coordinates. Solution: Using the conversion formulas, we have:
- x = 2 * cos(π/4) = √2
- y = 2 * sin(π/4) = √2
- z = 3
- x = 2 * cos(π/4) = √2
- y = 2 * sin(π/4) = √2
- z = 3
Therefore, the rectangular coordinates are (√2, √2, 3).
Example 2: Convert the rectangular coordinates (1, 1, 2) to cylindrical coordinates. Solution: Using the conversion formulas, we have:
- r = √(1² + 1²) = √2
- θ = tan^(-1)(1 / 1) = π/4
- z = 2
Therefore, the cylindrical coordinates are (√2, π/4, 2).
These examples illustrate how to convert coordinates between cylindrical and rectangular systems, providing a clear understanding of the process.
How Kunduz Can Help You Learn Cylindrical Coordinates?
At Kunduz, we understand the challenges of learning complex mathematical concepts. That’s why we offer comprehensive and accessible learning materials to help you master topics like cylindrical coordinates. Our expert tutors provide step-by-step explanations, solved examples, interactive exercises, and personalized guidance to ensure your success.
With Kunduz, you’ll have access to a wealth of resources, including video tutorials, practice problems, and real-time support. Our platform is designed to make learning mathematics engaging, interactive, and fun. Whether you’re a student, educator, or self-learner, Kunduz can help you navigate the intricacies of cylindrical coordinates and achieve your academic goals.
So why wait? Join Kunduz today and embark on a journey of mathematical discovery with our expert tutors by your side. Together, we’ll unlock the power of cylindrical coordinates and open doors to new realms of mathematical understanding.
