Decagons are fascinating geometric figures that play a crucial role in our understanding of the world around us. Whether it’s the shape of a star, a design element in architecture, or a mathematical problem to solve, decagons pop up in diverse areas of life and study. In this comprehensive guide, we’ll delve into the world of decagons, exploring their properties, formulas, types and more.
An Introduction to Decagon
A decagon is a captivating geometric figure that boasts ten sides and ten angles. It’s a closed, two-dimensional shape formed by ten straight line segments that meet at their endpoints. The term ‘decagon’ originates from the Latin words ‘deca’ meaning ten, and ‘gonia’ meaning angles. Hence, a decagon is a shape with ten angles. Each of these angles is created by the ten sides that form the polygon, and their sum is always equal to 1,440 degrees.
What is Decagon?
A decagon, in its simplest form, is a polygon with ten sides and ten vertices. It’s a two-dimensional shape that closes in a space. The term ‘decagon’ specifically refers to a regular decagon, a polygon with all sides and angles equal. However, the term can also refer to irregular decagons, where sides and angles are not necessarily equal.

Decagon Formula
Formulas are essential in understanding and calculating various aspects of a decagon. These include the area, perimeter, interior and exterior angles and more. Let’s explore these formulas in detail.
Area of a Decagon
The area of a regular decagon, a, can be calculated using the following formula:
Area (A) = 5/2 a² * √(5+2√5)
This formula combines geometry and trigonometry to determine the area enclosed by the decagon in relation to its side length.
Perimeter of a Decagon
The perimeter of a decagon, whether regular or irregular, is calculated by summing up the lengths of all its sides. This total distance around the decagon provides insight into its size and scale relative to its individual sides.
Measure of the Central Angles of a Regular Decagon
The central angle of a regular decagon can be found by dividing a full circle (360 degrees) by the number of sides (10). This results in each central angle measuring 36 degrees.
Number of Triangles and Lines of Symmetry in a Decagon
When we join one vertex to the remaining vertices of the decagon, we form eight triangles. Moreover, a regular decagon has ten lines of symmetry.
Formula to Find the Number of Sides of a Decagon
The number of sides of a decagon is determined by the sum of its interior angles. The formula to find the number of sides is:
Sum of interior angles/number of sides of a decagon (n)
Here, the sum is 1440° and n = 10, so each interior angle is 1440°/10 = 144°.
How To Construct a Decagon?
Constructing a decagon involves the following steps:
- Draw a circle using a compass.
- Mark a point on the circle as one vertex of the decagon.
- Using a protractor, divide the circle into ten equal parts, marking each division as a vertex.
- Connect all the vertices with straight lines to form the decagon.
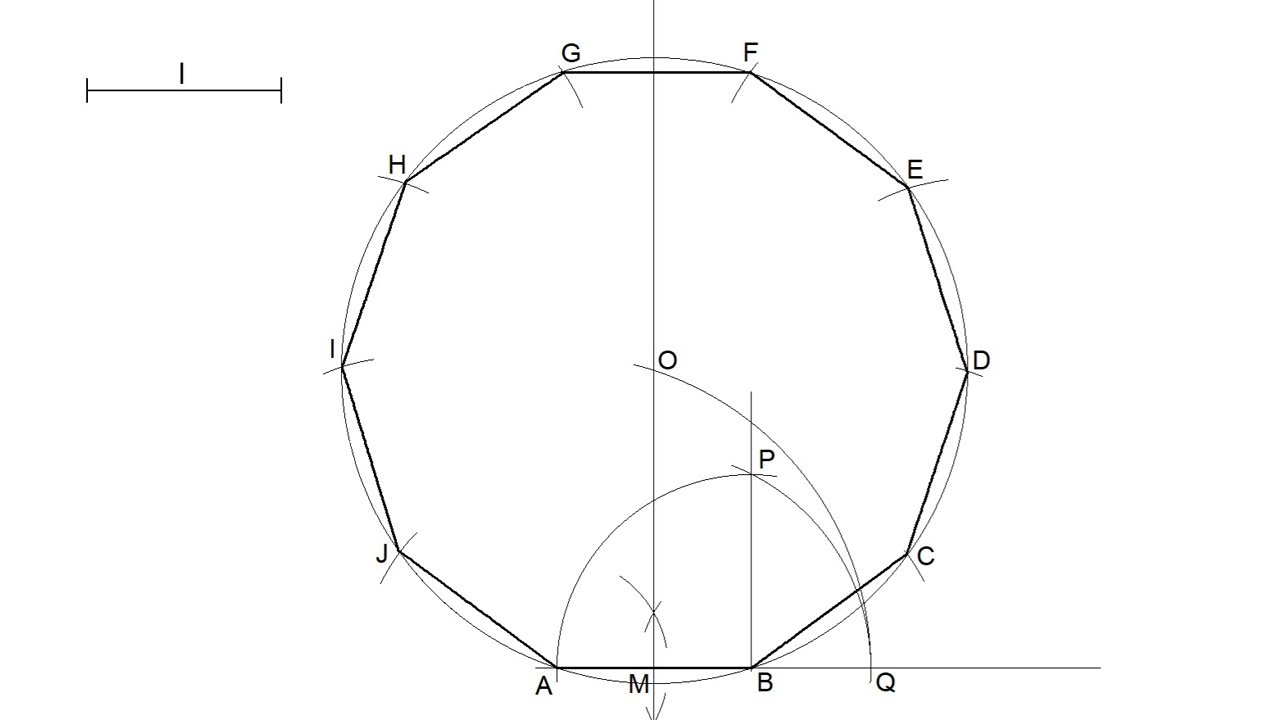
Types of Decagon
Decagons can be classified into various types based on their sides, vertices, and angles. Let’s explore these types in detail.
Regular Decagon
A regular decagon has all its sides and angles equal. The sides are congruent, and each angle measures exactly 144 degrees. This perfect symmetry results in a geometric shape that exudes elegance and mathematical beauty.
Irregular Decagon
An irregular decagon does not have all sides and angles equal. The sides and angles can vary, resulting in a diverse range of shapes.
Concave Decagon
A concave decagon has at least one interior angle exceeding 180 degrees. As a result, at least one vertex of the decagon points inwards.
Convex Decagons
A convex decagon has all its interior angles less than 180 degrees, and all its vertices point outwards.
Simple Decagon
A simple decagon is a decagon that has no sides crossing each other. It adheres to the regular decagon rules.
Complex Decagon
A complex decagon is a self-intersecting decagon that has additional interior spaces. It doesn’t strictly adhere to the regular decagon rules.
Angles of Decagon
The angles of a decagon are essential attributes that define its structure. Let’s delve into the various angles of a decagon.
Interior Angle
The interior angles of a decagon are the angles formed inside the decagon at its corners when the line segments join end to end.
Sum of Interior Angles
The sum of the interior angles of a decagon is always 1440 degrees. This sum reveals the underlying mathematical relationship between its angles.
One Interior Angle
The measure of one interior angle in a regular decagon can be found by dividing the sum of the interior angles by the number of sides. This results in each interior angle measuring 144 degrees.
Exterior Angle
An exterior angle of a decagon is the angle formed by any side of the decagon and the extension of its adjacent side. Each exterior angle of a regular decagon measures 36 degrees.
Properties of Decagon
Decagons possess unique properties that define their structure and mathematical relationships. Some of these properties include:
- Decagons have ten sides and ten angles.
- The sum of the interior angles of a decagon is 1440 degrees.
- A regular decagon has ten lines of symmetry.
- The total number of diagonals in a decagon is 35.
History and Significance of the Decagon
The decagon has held a significant place in history, particularly in the realms of art, architecture, and mathematics. Its ten sides and ten angles have made it a fascinating subject for study and exploration, leading to its incorporation in various designs and real-world applications.
Frequently Asked Questions on Decagon
What is a Decagon?
A decagon is a ten-sided polygon with ten vertices and ten angles. It can be regular, with all sides and angles equal, or irregular, with unequal sides and angles.
How Many Sides A Decagon Has?
A decagon, by definition, has ten sides.
What Does a Decagon Look Like?
A decagon is a ten-sided polygon. A regular decagon appears as a symmetrical shape with all sides and angles equal, while an irregular decagon can take on various shapes with unequal sides and angles.
What is the sum of the interior angles of a decagon?
The sum of the interior angles of a decagon is always 1440 degrees.
How do you find the Area of a Decagon?
The area of a regular decagon can be calculated using the formula A = (5a²) / (4 * tan(π/10)), where ‘a’ is the length of one side.
How Many Vertices and Diagonals Do a Regular Decagon Have?
A regular decagon has ten vertices and 35 diagonals.
What is a 10 Sided Shape Called?
A ten-sided shape is called a decagon.
Solved Examples on Decagon
To further solidify our understanding of decagons, let’s explore a couple of solved examples.
- Calculate the area of a regular decagon with a side length of 5 cm.
Using the formula A = (5a²) / (4 * tan(π/10)):
A = (5*5²) / (4 * tan(π/10)) ≈ 77.52 cm²
- Find the perimeter of a regular decagon with sides measuring 3 cm each.
The perimeter is the sum of all sides, so in this case, it’s 10*3 = 30 cm.
How Kunduz Can Help You Learn Decagon?
Kunduz is an innovative learning platform designed to help students grasp complex concepts like decagons effectively. It offers comprehensive resources and expert guidance to enable learners to discover the fascinating world of decagons and many other mathematical concepts. With Kunduz, you can transform your learning journey into an engaging and enjoyable adventure.
