Decimals play a significant role in various aspects of mathematics and daily life. They allow us to represent values that lie between whole numbers, enabling precise measurements and calculations. In this comprehensive guide, we will explore the definition, types, properties, and conversion of decimals, along with numerous examples to solidify our understanding.
An Introduction to Decimals
Decimals are a fundamental component of the number system. They provide a way to express fractional values, making them essential in fields such as science, finance, and engineering. A decimal number consists of two parts: the whole number part and the decimal fraction part. The decimal point separates these two components.
What is a Decimal?
A decimal is a numerical representation that combines a whole number and a fractional part. It is written using a decimal point, which separates the whole number from the fractional part. For example, the number 3.5 represents three whole units and half of another unit.

What are Decimal Numbers?
Decimal numbers are numbers that extend beyond whole numbers and include a fractional part. They are used to denote values that are not whole and provide a more precise representation of quantities. Decimal numbers are based on the decimal system, which has a base of 10 and uses the digits 0-9.
Types of Decimal Numbers
There are several types of decimal numbers, each with its own characteristics:
Recurring Decimal Numbers
Recurring decimals are numbers that have a repeating pattern of digits after the decimal point. The repeating pattern is denoted by placing a bar over the repeating part. For example, the decimal representation of the fraction 1/3 is 0.333…, where the digit 3 repeats infinitely.
Non-Recurring Decimal Numbers
Non-recurring decimals are numbers where the decimal expansion does not repeat. The digits after the decimal point do not form a recurring pattern. For example, the decimal representation of the fraction 1/4 is 0.25, where the digits 2 and 5 do not repeat.
Decimal Fractions
Decimal fractions are numbers that fall between two consecutive integers on the number line. They are expressed in decimal form and have a finite number of digits after the decimal point. For example, the number 0.75 represents three-fourths.
Terminating Decimals
Terminating decimals are decimal numbers that have a finite number of digits after the decimal point. They do not repeat or continue indefinitely. For example, the decimal representation of the fraction 1/2 is 0.5.
Non-Terminating Decimals
Non-terminating decimals are decimal numbers that have an infinite number of digits after the decimal point. They can either have a repeating pattern or a non-repeating pattern. For example, the decimal representation of the fraction 1/3 is 0.333…, where the digit 3 repeats infinitely.
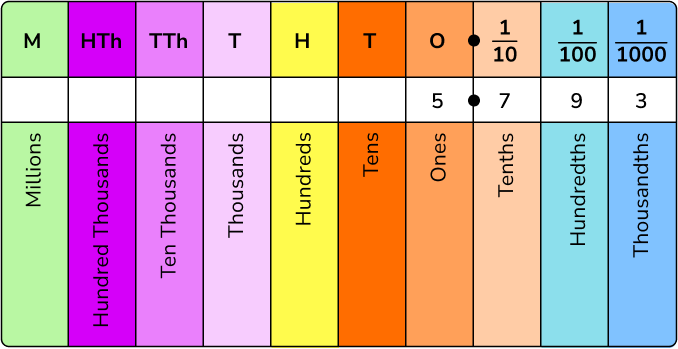
Place Value in Decimals
The place value system in decimals is similar to the whole number system. Each digit in a decimal number has a specific place value based on its position relative to the decimal point. The place value of a digit in a decimal number is determined by the power of 10 associated with its position.
Understanding the place value in decimals is crucial for dealing with these numbers. Each digit in a decimal number has a specific place value. For instance, in the decimal number 78.325, 7 is in the tens place, 8 is in the ones place, 3 is in the tenths place, 2 is in the hundredths place, and 5 is in the thousandths place.
As we move from left to right in the decimal place value system, each value becomes 10 times smaller than the value to its left.
Properties of Decimals
Decimals possess several properties that govern their behavior in mathematical operations. Here are some important properties of decimals:
- Closure Property: The sum or difference of two decimals is always a decimal.
- Commutative Property: The order of the decimals does not affect the result of addition or multiplication. For example, a + b = b + a and a × b = b × a.
- Associative Property: The grouping of decimals does not affect the result of addition or multiplication. For example, (a + b) + c = a + (b + c) and (a × b) × c = a × (b × c).
- Identity Property: The sum of a decimal and zero is the decimal itself. For example, a + 0 = a. The product of a decimal and one is the decimal itself. For example, a × 1 = a.
- Distributive Property: The product of a decimal and the sum of two other decimals is equal to the sum of the products of the decimal with each of the other decimals. For example, a × (b + c) = (a × b) + (a × c).
- Inverse Property: The sum of a decimal and its additive inverse (negative) is zero. For example, a + (-a) = 0.
- Identity Element: The decimal 0 serves as the additive identity element, as a + 0 = a for any decimal a. The decimal 1 serves as the multiplicative identity element, as a × 1 = a for any decimal a.
Arithmetic Operations on Decimals
Decimals can be operated upon using various arithmetic operations, including addition, subtraction, multiplication, and division.
Addition
To add decimals, align them vertically based on the decimal point and add the digits in each column, starting from the rightmost column. Carry over any excess values to the next column if necessary. Finally, place the decimal point in the sum directly below the decimal point in the given decimals.
Subtraction
To subtract decimals, align them vertically based on the decimal point and subtract the digits in each column, starting from the rightmost column. Borrow from the next column if necessary. Place the decimal point in the difference directly below the decimal point in the given decimals.
Multiplication
To multiply decimals, ignore the decimal points initially and multiply the numbers as if they were whole numbers. Count the total decimal places in the factors and place the decimal point in the product, counting from the right, equal to the total decimal places.
Division
To divide decimals, divide the numbers as if they were whole numbers, ignoring the decimal point. Count the total decimal places in both the dividend and divisor. Move the decimal point in the quotient to make it a whole number, then adjust accordingly.
Decimal to Fraction Conversion
Converting a decimal to a fraction involves expressing the decimal as a ratio of two integers. The numerator of the fraction is obtained by removing the decimal point, and the denominator is determined by the number of decimal places. Simplify the fraction if possible.
Fraction to Decimal Conversion
Converting a fraction to a decimal involves dividing the numerator by the denominator. If the division terminates, the resulting decimal is terminating. If the division repeats, the resulting decimal is recurring.
Binary to Decimal Conversion
To convert a binary number to a decimal number, multiply each binary digit by the corresponding power of 2 and sum the results.
Decimal to Binary Conversion
To convert a decimal number to a binary number, divide the decimal number by 2 repeatedly, noting the remainders. The binary equivalent is obtained by reading the remainders in reverse order.
Octal to Decimal Conversion
To convert an octal number to a decimal number, multiply each octal digit by the corresponding power of 8 and sum the results.
Decimal to Octal Conversion
To convert a decimal number to an octal number, divide the decimal number by 8 repeatedly, noting the remainders. The octal equivalent is obtained by reading the remainders in reverse order.
Hexadecimal to Decimal Conversion
To convert a hexadecimal number to a decimal number, multiply each hexadecimal digit by the corresponding power of 16 and sum the results.
Decimal to Hexadecimal Conversion
To convert a decimal number to a hexadecimal number, divide the decimal number by 16 repeatedly, noting the remainders. The hexadecimal equivalent is obtained by reading the remainders in reverse order and replacing values greater than 9 with the corresponding letters A-F.
Expanded Form of Decimal Numbers
The expanded form of a decimal number shows the value of each digit based on its place value. It is expressed as the sum of each digit multiplied by the corresponding power of 10.
Rounding Decimal Numbers to the Nearest Tenths
Rounding a decimal number to the nearest tenth involves examining the digit in the hundredths place. If the digit is 4 or less, round down to the nearest tenth. If the digit is 5 or greater, round up to the nearest tenth.
How to Compare Decimals?
To compare decimals, start by comparing the whole number part. If they are equal, compare the tenths place, then the hundredths place, and so on. The decimal with the larger digit in the first differing place value is greater.
How to Read Decimal Numbers?
Decimal numbers can be read in two ways. The first method is to read the whole number part, followed by “point,” and then read the digits of the fractional part separately. The second method is to read the whole number part first, then the fractional part, using the place value of the last digit of the fractional part.
How Kunduz Can Help You Learn Decimals?
At Kunduz, we understand the importance of mastering decimal numbers. We offer a wide range of resources and tools to help you learn and practice decimals effectively. Our interactive lessons, practice exercises, and personalized feedback will guide you towards a comprehensive understanding of decimals. Join us at Kunduz and embark on an exciting journey of decimal learning.
