The derivative is a fundamental concept in calculus that measures the rate of change of a function at a particular point. In this article, we will explore the derivative of arcsin (also known as the inverse sine function) and its properties.
The arcsin function is the inverse of the sine function. It returns the angle whose sine is a given number. The derivative of arcsin allows us to determine the rate at which the arcsin function changes with respect to its input variable.
What is Arcsin?
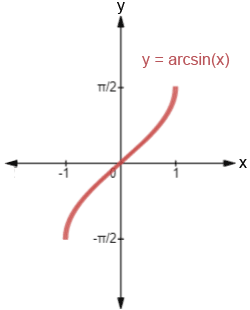
Arcsin, also denoted as sin⁻¹, is the inverse function of the sine function. This function is used to determine the angle whose sine is a given number. The arcsin function can only take values between -1 and 1, and it will return an angle in the interval from -π/2 to π/2 (or -90° to 90°), inclusive.
What is the Derivative of Arcsin?
The derivative of arcsin x, written as d/dx(arcsin x) or (arcsin x)’, is 1/√1-x². It represents the rate of change of the arcsin function with respect to x. This means that for a tiny change in x, the derivative gives the corresponding tiny change in the arcsin x.
Derivative of Arcsin Formula
The derivative of arcsin x, denoted by d/dx(arcsin x), is given by the formula 1/√1 – x². It signifies the rate at which the arcsin x changes as x changes. The formula is derived from the general definition of derivatives and the properties of sine and its inverse function, arcsin.
Proof of Derivative of Arcsin x
The derivative of arcsin x can also be proven using different methods, such as the quotient rule, chain rule, or first principle of differentiation. Let’s explore these proofs in detail:
Proof of Derivative of Arcsin by Quotient Rule
To prove the derivative of arcsin x using the quotient rule, we start with the equation sin y = x, where y = arcsin x. Differentiating both sides of the equation with respect to x, we get:
d/dx(sin y) = d/dx(x)
Using the chain rule, the left side becomes:
cos y * dy/dx = 1
Solving for dy/dx, we get:
dy/dx = 1/cos y
To express cos y in terms of x, we can use a reference triangle. In the reference triangle, the opposite side is x and the hypotenuse is 1. Thus, cos y = √(1 – x^2). Substituting this into the equation, we get:
dy/dx = 1/√(1 – x^2)
This is the derivative of arcsin x.
Proof of Derivative of Arcsin by Chain Rule
Another way to prove the derivative of arcsin x is by using the chain rule. Starting with the equation sin y = x, we differentiate both sides with respect to x:
d/dx(sin y) = d/dx(x)
Using the chain rule, the left side becomes:
cos y * dy/dx = 1
Solving for dy/dx, we get:
dy/dx = 1/cos y
To express cos y in terms of x, we can rewrite the equation as cos y = √(1 – sin^2 y). Since sin y = x, we have cos y = √(1 – x^2). Substituting this into the equation, we get:
dy/dx = 1/√(1 – x^2)
This is the derivative of arcsin x.
Proof of Derivative of Arcsin by First Principle
The first principle of differentiation can also be used to prove the derivative of arcsin x. Starting with the definition of arcsin x as sin y = x, we can apply the first principle of differentiation:
f'(x) = lim(h->0) [f(x + h) – f(x)] / h
Substituting arcsin x for f(x), we get:
d/dx(arcsin x) = lim(h->0) [arcsin(x + h) – arcsin x] / h
We can rewrite this equation as:
d/dx(arcsin x) = lim(h->0) [sin(arcsin(x + h)) – sin(arcsin x)] / h
Since sin(arcsin x) = x, the equation simplifies to:
d/dx(arcsin x) = lim(h->0) [(x + h) – x] / h
Simplifying further, we have:
d/dx(arcsin x) = lim(h->0) h / h
Which reduces to:
d/dx(arcsin x) = 1
This proves that the derivative of arcsin x is equal to 1.
Properties of Arcsine
Arcsin has several properties that are important to understand. These properties include:
- Domain and Range: The domain of arcsin is [-1, 1], which means that it is defined for values of x between -1 and 1. The range of arcsin is [-π/2, π/2] in radians or [-90°, 90°] in degrees.
- Symmetry: Arcsin has odd symmetry, which means that arcsin(-x) = -arcsin(x). This property reflects the fact that the sine function is an odd function.
- Inverse of Sine: Arcsin is the inverse function of the sine function. This means that if y = arcsin(x), then sin(y) = x.
- Monotonicity: Arcsin is a strictly increasing function on its domain. This means that as x increases, arcsin(x) also increases.
- Inflection Point: Arcsin has an inflection point at x = 0, where the concavity changes from positive to negative.
Solved Examples on Derivative of Arcsin
Let’s now solve some examples to better understand the derivative of arcsin.
Example 1: Find the derivative of y = arcsin(2x).
Solution: To find the derivative, we can apply the chain rule. Let’s denote y as arcsin(2x). Using the chain rule, we have:
dy/dx = d/dx(arcsin(2x)) = (1/√(1 – (2x)^2)) * d/dx(2x)
Simplifying, we get:
dy/dx = (1/√(1 – 4x^2)) * 2
dy/dx = 2/√(1 – 4x^2)
Example 2: Find the derivative of y = arcsin(x^2 + 1).
Solution: Again, we can apply the chain rule to find the derivative. Let’s denote y as arcsin(x^2 + 1). Using the chain rule, we have:
dy/dx = d/dx(arcsin(x^2 + 1)) = (1/√(1 – (x^2 + 1)^2)) * d/dx(x^2 + 1)
Simplifying, we get:
dy/dx = (1/√(1 – (x^2 + 1)^2)) * 2x
dy/dx = 2x/√(1 – (x^2 + 1)^2)
These examples demonstrate how to calculate the derivatives of more complex expressions involving arcsin.
How Kunduz Can Help You Learn Derivatives of Arcsin?
With a plethora of resources available, learning derivatives of arcsin can be a breeze. Kunduz, for instance, offers a wide range of learning materials, practice problems, and solutions to help students master the concept of derivatives, including those of arcsin. Whether you’re a beginner or an advanced learner, Kunduz can provide you with the right tools and resources to enhance your understanding of derivatives and their applications in various fields.
Related Topics:
