Differentiation is a fundamental concept in calculus that allows us to find the rate of change of a function with respect to its independent variable. When it comes to trigonometric functions, differentiation plays a crucial role in understanding their behavior and analyzing various real-world applications. In this article, we will delve into the intricacies of differentiation of trigonometric functions, exploring their formulas, proofs, and applications. By the end, you will have a solid understanding of how to find the derivatives of trigonometric functions and apply them in solving problems.
What is the Differentiation of Trigonometric Functions?
Differentiation of trigonometric functions involves finding the rate of change of these functions with respect to the angle. The six basic trigonometric functions include sine (sin x), cosine (cos x), tangent (tan x), cotangent (cot x), secant (sec x), and cosecant (csc x). Each of these functions has a specific derivative formula, which allows us to calculate their derivatives.
The derivative of a function represents its instantaneous rate of change at a specific point. In the case of trigonometric functions, the derivatives provide valuable information about the slopes of tangent lines to their graphs. These slopes indicate the rates at which the functions are increasing or decreasing at different angles.
Proof of Differentiation of Trigonometric Functions Formula
To understand the derivatives of trigonometric functions, let’s explore their proofs. We will start with the derivatives of the sine and cosine functions, which are fundamental to the differentiation of trigonometric functions.
Derivative of Sin(x)
The derivative of the sine function, denoted as d/dx(sin x), is equal to the cosine function, cos x. This can be proven using the first principle of differentiation and trigonometric identities.
To derive the derivative of sin x, we start with the definition of the derivative:
d/dx(sin x) = lim(h→0) [(sin(x + h) – sin x) / h]
Expanding the expression using the trigonometric identity for the sine of the sum of two angles, we get:
d/dx(sin x) = lim(h→0) [(sin x cos h + cos x sin h – sin x) / h]
By factoring out sin x and applying limit formulas, we simplify the expression to:
d/dx(sin x) = cos x
Therefore, the derivative of sin x is equal to cos x.
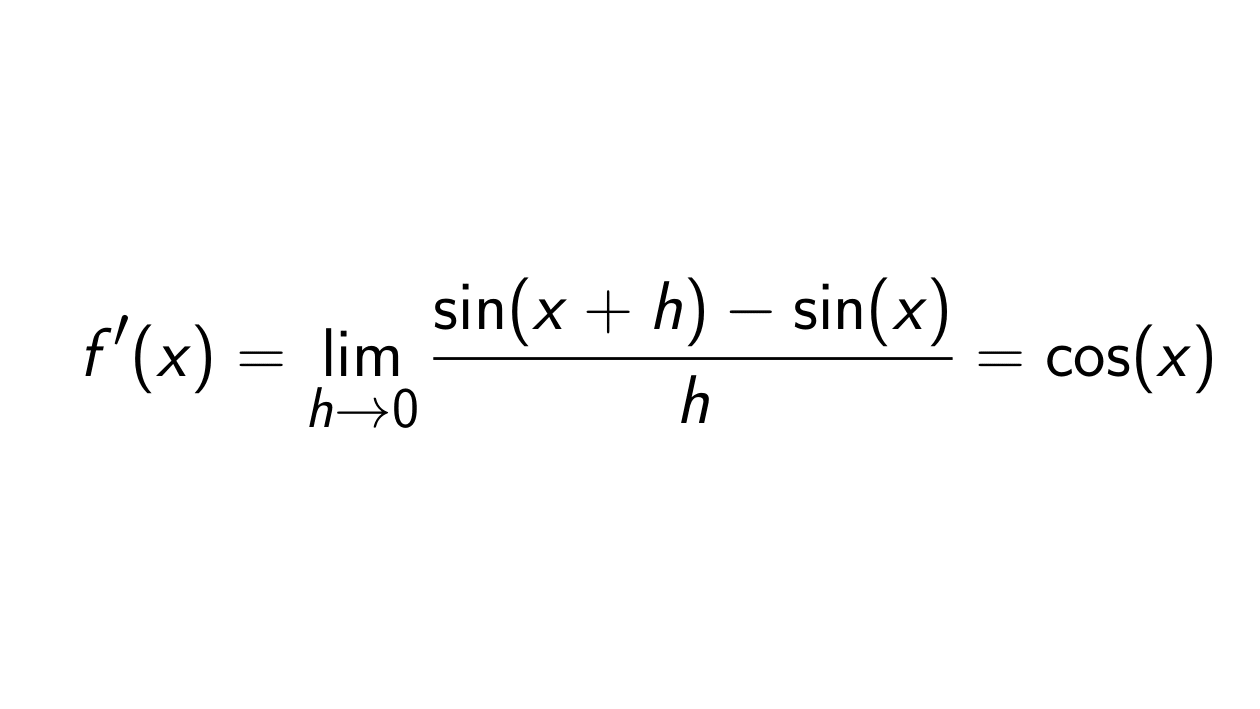
Derivative of Cos(x)
Similar to the derivative of sin x, the derivative of the cosine function, d/dx(cos x), is equal to the negative sine function, -sin x. This can also be proven using the first principle of differentiation and trigonometric identities.
Starting with the definition of the derivative:
d/dx(cos x) = lim(h→0) [(cos(x + h) – cos x) / h]
Expanding the expression using the trigonometric identity for the cosine of the sum of two angles, we get:
d/dx(cos x) = lim(h→0) [(cos x cos h – sin x sin h – cos x) / h]
By factoring out cos x and applying limit formulas, we simplify the expression to:
d/dx(cos x) = -sin x
Therefore, the derivative of cos x is equal to -sin x.
![Derivative of cos(x) using First Principle of Derivatives - [FULL PROOF]](https://www.epsilonify.com/wp-content/uploads/2022/09/Derivative-of-cosx-using-First-Principle-Method-1.png)
Derivative of Tan(x)
The derivative of tan(x) is sec² x. The tan function can be expressed as the ratio of sin x and cos x. Using the quotient rule of differentiation, we get:
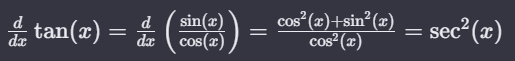
The derivative of the tangent function with respect to x is equal to the derivative of the ratio of sine to cosine, which simplifies to the ratio of the sum of the squares of cosine and sine to the square of cosine, resulting in the secant squared of x.
Derivative of Cot(x)
The derivative of cot x is -cosec² x. The cot function can be expressed as the ratio of cos x to sin x. Using the quotient rule of differentiation, we get:
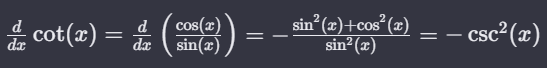
The derivative of the cotangent function with respect to x is equal to the derivative of the ratio of cosine to sine, which simplifies to the negative ratio of the sum of the squares of sine and cosine to the square of sine, resulting in the negative cosecant squared of x.
Derivative of Sec(x)
The derivative of sec x is sec x tan x. The sec function can be expressed as the reciprocal of cos x. Using the chain rule of differentiation, we get:
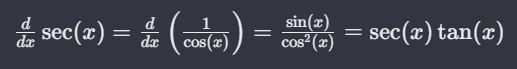
The derivative of the secant function with respect to x is equal to the derivative of the reciprocal of cosine, which simplifies to the ratio of sine to the square of cosine, resulting in the product of secant and tangent of x.
Derivative of Cosec(x)
The derivative of cosec x is -cosec x cot x. The cosec function can be expressed as the reciprocal of sin x. Using the chain rule of differentiation, we get:
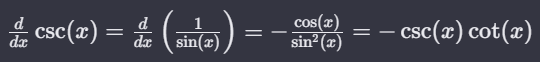
The derivative of the cosecant function with respect to x is equal to the derivative of the reciprocal of sine, which simplifies to the negative ratio of cosine to the square of sine, resulting in the negative product of cosecant and cotangent of x.
Table of Derivatives of Trigonometric Functions
The derivatives of the six basic trigonometric functions can be summarized using the following formulas:
| Function | Derivative |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| tan(x) | sec²(x) |
| cot(x) | -cosec²(x) |
| sec(x) | sec(x)tan(x) |
| cosec(x) | -cosec(x)cot(x) |
These formulas provide a systematic way to find the derivatives of trigonometric functions and apply them in various mathematical and physical problems.
Higher-Order Derivatives
In addition to finding the first derivative of trigonometric functions, we can also calculate higher-order derivatives. This involves differentiating the functions multiple times to find their rates of change at higher levels.
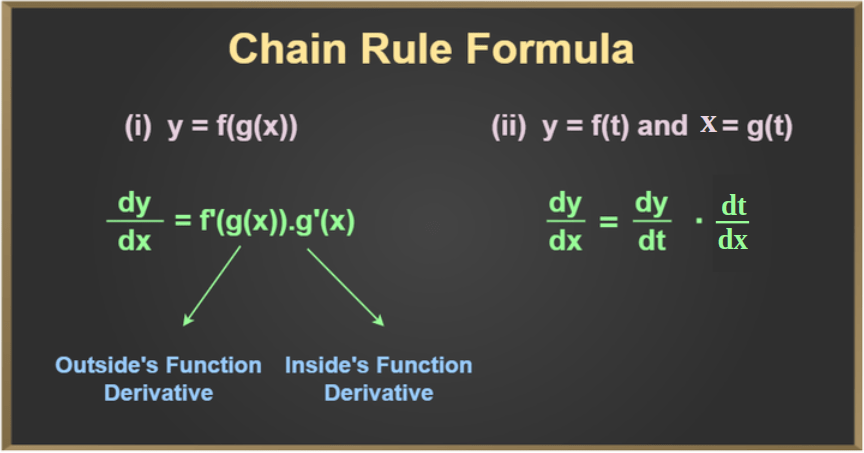
Chain Rule and Trigonometric Function
The chain rule of differentiation is a crucial technique when dealing with composite functions. When applying the chain rule to trigonometric functions, we differentiate the outer function and multiply it by the derivative of the inner function.
For example, if we have a function f(x) = sin(3x), we can find its derivative by applying the chain rule:
d/dx(sin(3x)) = cos(3x) * d/dx(3x) = 3cos(3x)
Differentiation of Composite Trig Function
In some cases, we may encounter composite trigonometric functions, where trigonometric functions are combined with other functions. To differentiate these functions, we apply the chain rule and the derivative rules for trigonometric functions.
For example, if we have a function f(x) = sin(x^2), we differentiate it using the chain rule:
d/dx(sin(x²)) = cos(x²) * d/dx(x²) = 2x*cos(x²)
These techniques allow us to find the derivatives of trigonometric functions in more complex scenarios.
Solved Examples on Differentiation of Trigonometric Functions
Let’s now explore some solved examples to further understand the application of differentiation of trigonometric functions.
Example 1: Find the derivative of the function f(x) = 2sin(x) + 3cos(x).
Solution: To find the derivative of f(x), we differentiate each term separately using the derivative formulas for trigonometric functions:
d/dx(2sin(x) + 3cos(x)) = 2cos(x) – 3sin(x)
Therefore, the derivative of f(x) is 2cos(x) – 3sin(x).
Example 2: Find the derivative of the function g(x) = tan(x) * sec(x).
Solution: Using the product rule of differentiation, we differentiate each term separately and then combine them:
d/dx(tan(x) * sec(x)) = sec²(x) * sec(x) + tan(x) * sec(x) * tan(x)
Simplifying the expression, we get:
d/dx(tan(x) * sec(x)) = sec³(x) + tan²(x) * sec(x)
Therefore, the derivative of g(x) is sec³(x) + tan²(x) * sec(x).
Applications of Differentiation of Trigonometric Functions
The differentiation of trigonometric functions has wide-ranging applications in various fields. Some of the key applications include:
- Physics: Differentiation of trigonometric functions is crucial in analyzing motion and mechanical systems. It helps us understand the velocity, acceleration, and forces acting on objects undergoing simple harmonic motion or rotational motion.
- Engineering: Trigonometric functions play a vital role in engineering applications, such as signal processing, control systems, and electrical circuit analysis. Differentiation allows engineers to analyze and optimize these systems for better performance.
- Mathematics: Trigonometric functions and their derivatives are essential in mathematical modeling and solving differential equations. They are used to describe various periodic phenomena and oscillatory behavior in nature.
- Computer Science: Trigonometric functions and their derivatives are utilized in computer graphics, image processing, and animation. They help create realistic visual effects and simulate complex motions.
Differentiation of Inverse Trigonometric Functions
In addition to differentiating trigonometric functions, we can also find the derivatives of their inverse functions, known as inverse trigonometric functions. These include arcsin(x), arccos(x), arctan(x), arccsc(x), arcsec(x), and arccot(x).
The derivatives of inverse trigonometric functions can be derived using the chain rule and the derivatives of their corresponding trigonometric functions. For example:
- d/dx(arcsin(x)) = 1 / √(1 – x²)
- d/dx(arccos(x)) = -1 / √(1 – x²)
- d/dx(arctan(x)) = 1 / (1 + x²)
- d/dx(arccsc(x)) = -1 / (|x| * √(x² – 1))
- d/dx(arcsec(x)) = 1 / (|x| * √(x² – 1))
- d/dx(arccot(x)) = -1 / (1 + x²)
These formulas allow us to find the derivatives of inverse trigonometric functions and solve problems involving these functions.

Anti-Differentiation of Trigonometric Functions
Anti-differentiation, also known as integration, is the inverse process of differentiation. It involves finding the original function, or the indefinite integral, given its derivative. The anti-derivatives of trigonometric functions are known as trigonometric integrals.
The anti-derivatives of trigonometric functions can be calculated using well-known integration techniques, such as substitution, integration by parts, and trigonometric identities. These techniques allow us to find the original function when its derivative is a trigonometric function.
In conclusion, the differentiation of trigonometric functions is a fundamental concept in calculus that allows us to find the rate of change of these functions. By applying the derivative formulas and rules, we can calculate the derivatives of trigonometric functions and use them in various mathematical, scientific, and engineering applications. Understanding the derivatives of trigonometric functions is crucial for analyzing motion, solving differential equations, and modeling periodic phenomena.
