In mathematics, functions are essential tools for understanding relationships between variables. They allow us to input different values and obtain corresponding outputs. Two key components of functions are the domain and range. The domain represents the set of possible input values, while the range represents the set of possible output values. Understanding how to find the domain and range of a function is crucial for analyzing and interpreting mathematical relationships.
An Introduction to Domain and Range
Before we delve into finding the domain and range of a function, let’s first understand what these terms mean. The domain of a function is the set of all possible input values, or the values for which the function is defined. The range, on the other hand, is the set of all possible output values that the function can produce. In simpler terms, the domain refers to the values we can “plug into” the function, while the range refers to the values we can obtain as the result.
To illustrate this concept, let’s consider a function as a vending machine. When we insert a specific amount of money, we can select different types of sodas. In this analogy, the domain would represent the valid denominations of coins and bills that can be inserted into the machine, while the range would correspond to the different flavors of sodas available.
What is Domain?
The domain of a function is the set of all possible input values that the function can accept. It represents the values for which the function is defined. Just like how a soda machine only accepts certain denominations of coins and bills, a function has certain limitations on the values it can take as input.
The domain can vary depending on the type of function and any specific constraints or restrictions that may be present. For example, a linear function, such as f(x) = 2x + 1, has a domain of all real numbers because it is defined for any value of x. On the other hand, a square root function, such as f(x) = √x, has a domain of x ≥ 0 because the square root of a negative number is undefined in the real number system.
It is important to note that the domain should be expressed in a way that reflects any restrictions or limitations imposed by the function. This ensures that the function is well-defined and meaningful for the given input values.
What is Range?
The range of a function is the set of all possible output values that the function can produce. It represents the values that the function can “output” or yield based on the given input values. Similar to how a soda machine offers different flavors of soda as output, a function produces different values as output based on the input.
The range of a function can vary depending on the type of function and the specific values it can produce. For example, a linear function, such as f(x) = 2x + 1, has a range of all real numbers because it can produce any real number as an output. However, a square root function, such as f(x) = √x, has a range of y ≥ 0 because the square root of a negative number is undefined in the real number system.
It is important to note that the range should be expressed in a way that reflects the possible output values of the function. This ensures that the range accurately represents the values that the function can produce.
Domain and Range of a Function
Now that we have a basic understanding of domain and range, let’s explore how to determine the domain and range of a function. The domain and range of a function depend on the specific characteristics and properties of the function.
Domain of a Function
The domain of a function represents the set of all possible input values for which the function is defined. It is important to identify any restrictions or limitations on the input values that may exist within the given function. The domain of a function can be determined using various rules and techniques.
Rules of Finding Domain of a Function
There are certain rules that can help us determine the domain of different types of functions. These rules provide guidelines for identifying any restrictions or limitations on the input values. Let’s explore some of the common rules for finding the domain of a function:
- Polynomial Functions: The domain of polynomial functions, such as linear, quadratic, cubic, etc., is all real numbers (ℝ). There are no restrictions on the input values for these types of functions.
- Square Root Functions: The domain of a square root function, such as f(x) = √x, is x ≥ 0. This is because the square root of a negative number is undefined in the real number system.
- Exponential Functions: The domain of an exponential function, such as f(x) = ax, is all real numbers (ℝ). Exponential functions are defined for any value of x.
- Logarithmic Functions: The domain of a logarithmic function, such as f(x) = log(x), is x > 0. Logarithmic functions are defined only for positive values of x.
- Rational Functions: The domain of a rational function, such as f(x) = 1/x, is determined by the denominator. The function is defined for all x-values except those that make the denominator equal to zero. To find the domain of a rational function, set the denominator ≠ 0.
These rules provide a general framework for determining the domain of different types of functions. By understanding the specific characteristics and restrictions of the function, we can accurately identify the domain and ensure that the function is well-defined for the given input values.
How to Find the Domain of a Function?
To find the domain of a function, we need to analyze the given function and identify any restrictions or limitations on the input values. Here is a step-by-step process for finding the domain of a function:
Step 1: Identify any restrictions or limitations on the input values. Look for any values that would make the function undefined or result in an error.
Step 2: Consider the specific characteristics and properties of the function. For example, if the function involves a square root, logarithm, or rational expression, there may be restrictions on the input values.
Step 3: Determine the set of input values that satisfy the restrictions or limitations. This set of values represents the domain of the function.
Step 4: Express the domain in the appropriate notation. Depending on the context, the domain can be expressed in interval notation, set-builder notation, or other appropriate formats.
By following this step-by-step process, we can systematically determine the domain of a function and ensure that the function is well-defined for the given input values.
Finding the Domain of a Function Defined by an Equation
Let’s consider an example to illustrate how to find the domain of a function defined by an equation. Suppose we have the function f(x) = 1 / (x – 2). To find the domain of this function, we need to identify any restrictions on the input values.
In this case, we can see that the denominator of the function is x – 2. To ensure that the denominator is not equal to zero (since division by zero is undefined), we need to find the values of x that make the denominator zero. In this case, x = 2 is the value that makes the denominator zero.
Therefore, the domain of the function f(x) = 1 / (x – 2) is all real numbers except x = 2. We can express the domain in interval notation as (-∞, 2) ∪ (2, ∞).
By identifying the restriction on the input value, we can accurately determine the domain of the function and ensure that it is well-defined for the given input values.
Finding the Domain of a Function as a Set of Ordered Pairs
In some cases, the domain of a function may be defined by a set of ordered pairs. To find the domain in this situation, we need to consider the x-coordinates of the ordered pairs.
Let’s consider an example to illustrate this concept. Suppose we have the function f = {(1, 2), (2, 3), (3, 4), (4, 5)}. To find the domain of this function, we need to consider the x-coordinates of the ordered pairs.
From the given set of ordered pairs, we can see that the x-coordinates are 1, 2, 3, and 4. Therefore, the domain of the function f is {1, 2, 3, 4}.
By considering the x-coordinates of the ordered pairs, we can determine the domain of the function and identify the valid input values for the function.
Finding the Domain of a Function Involving a Denominator
When a function involves a denominator, there may be restrictions on the input values to avoid division by zero. To find the domain in this situation, we need to set the denominator of the function to be not equal to zero and solve for the input values.
Let’s consider an example to illustrate this concept. Suppose we have the function f(x) = 1 / (x + 1). To find the domain of this function, we need to consider the values of x that make the denominator, x + 1, not equal to zero.
In this case, to avoid division by zero, we set the denominator x + 1 not equal to zero and solve for x:
x + 1 ≠ 0
x ≠ -1
Therefore, the domain of the function f(x) = 1 / (x + 1) is all real numbers except x = -1. We can express the domain in interval notation as (-∞, -1) ∪ (-1, ∞).
By considering the restrictions on the input values and avoiding division by zero, we can accurately determine the domain of the function and ensure that it is well-defined.
Range of a Function
The range of a function represents the set of all possible output values that the function can produce. It is important to identify the range to understand the full range of values that the function can yield.
To find the range of a function, we need to analyze the behavior and characteristics of the function and determine the set of possible output values. The range can vary depending on the type of function and the specific values it can produce.
Rules of Finding Range of a Function
There are certain rules that can help us determine the range of different types of functions. These rules provide guidelines for identifying the set of possible output values. Let’s explore some of the common rules for finding the range of a function:
- Linear Functions: The range of a linear function, such as f(x) = mx + b, is all real numbers (ℝ). Linear functions can produce any real number as an output.
- Quadratic Functions: The range of a quadratic function, such as f(x) = ax^2 + bx + c, depends on the direction of the quadratic curve. If the parabola opens upward and the leading coefficient is positive (a > 0), the range is y ≥ k, where k is the y-coordinate of the vertex. If the parabola opens downward and the leading coefficient is negative (a < 0), the range is y ≤ k.
- Exponential Functions: The range of an exponential function, such as f(x) = a^x, is y > 0. Exponential functions always produce positive values.
- Logarithmic Functions: The range of a logarithmic function, such as f(x) = log(x), is all real numbers (ℝ). Logarithmic functions can produce any real number as an output.
- Square Root Functions: The range of a square root function, such as f(x) = √x, is y ≥ 0. Square root functions always produce non-negative values.
These rules provide a general framework for determining the range of different types of functions. By understanding the specific characteristics and properties of the function, we can accurately identify the range and ensure that it represents the set of possible output values.
How to Find the Range of a Function?
To find the range of a function, we need to analyze the given function and identify the set of possible output values. Here is a step-by-step process for finding the range of a function:
Step 1: Analyze the behavior and properties of the function. Consider any restrictions or limitations on the output values.
Step 2: Determine the set of possible output values based on the specific characteristics of the function. Consider any restrictions or limitations on the output values.
Step 3: Express the range in the appropriate notation. Depending on the context, the range can be expressed in interval notation, set-builder notation, or other appropriate formats.
By following this step-by-step process, we can systematically determine the range of a function and accurately represent the set of possible output values.
Co-Domain and Range
In addition to the domain and range, it is also important to understand the concepts of co-domain and range. The co-domain of a function represents the set of all possible output values, while the range represents the subset of the co-domain that is actually produced by the function.
For example, consider a function f: A → B, where A is the domain and B is the co-domain. The co-domain includes all possible output values that the function can produce. However, the range represents the subset of the co-domain that is actually produced by the function.
To illustrate this concept, let’s consider a function f: x → x^2, where x is a real number. The co-domain of this function is the set of all real numbers (ℝ), as any real number can be squared. However, the range of this function is the set of non-negative real numbers, as squaring a negative number would result in a positive value.
Understanding the co-domain and range helps to clarify the relationship between the possible output values and the actual output values produced by a function. It provides a more comprehensive understanding of the function’s behavior and properties.
How To Calculate Domain And Range?
Calculating the domain and range of a function involves analyzing the specific characteristics and properties of the function. By understanding the rules and guidelines for different types of functions, we can systematically determine the domain and range.
To calculate the domain and range of a function, follow these steps:
Step 1: Identify the type of function you are working with. Consider whether it is a polynomial function, exponential function, logarithmic function, etc.
Step 2: Apply the specific rules and guidelines for finding the domain and range of that type of function. Consider any restrictions or limitations on the input or output values.
Step 3: Solve any equations or inequalities that arise from the specific rules and guidelines. This will help determine the set of valid input or output values.
Step 4: Express the domain and range in the appropriate notation. Depending on the context, this can be interval notation, set-builder notation, or other appropriate formats.
By following these steps and applying the appropriate rules and guidelines, you can accurately calculate the domain and range of a function.
Domain and Range of Exponential Functions
Exponential functions are functions of the form f(x) = a^x, where a is a constant and x is the input value. The domain and range of exponential functions depend on the specific value of a and the restrictions or limitations on the input and output values.
The domain of an exponential function is all real numbers (ℝ). Exponential functions are defined for any value of x, as long as a is a positive number. The range of an exponential function is y > 0, as exponential functions always produce positive values.
For example, consider the function f(x) = 2^x. The domain of this function is all real numbers (ℝ), as it is defined for any value of x. The range of this function is y > 0, as exponential functions always produce positive values.
It is important to consider the specific value of a and any restrictions or limitations on the input and output values when determining the domain and range of exponential functions. By understanding the behavior and properties of exponential functions, we can accurately calculate their domain and range.
Domain and Range of Trigonometric Functions
Trigonometric functions are functions that involve the ratios of the sides of a right triangle. The domain and range of trigonometric functions depend on the specific trigonometric function and the restrictions or limitations on the input and output values.
The domain of trigonometric functions is all real numbers (ℝ), as they are defined for any value of the input angle. However, there may be specific restrictions on the input values for certain trigonometric functions. For example, the domain of the tangent function is ℝ – (2n + 1)π/2, where n is an integer. This is because the tangent function is undefined for angles that are odd multiples of π/2.
The range of trigonometric functions varies depending on the specific trigonometric function. For the sine and cosine functions, the range is [-1, 1]. This is because the sine and cosine functions produce values between -1 and 1 as the input angle varies. The range of other trigonometric functions, such as secant, cosecant, tangent, and cotangent, can vary depending on the specific function.
It is important to consider the specific trigonometric function and any restrictions or limitations on the input and output values when determining the domain and range of trigonometric functions. By understanding the behavior and properties of trigonometric functions, we can accurately calculate their domain and range.
Trigonometric Functions, Domain, Range (Table)
| Trigonometric Function | Domain | Range |
|---|---|---|
| sin θ | ℝ | [-1, 1] |
| cos θ | ℝ | [-1, 1] |
| tan θ | ℝ – (2n + 1)π/2 | ℝ |
| cot θ | ℝ – nπ | ℝ |
| sec θ | ℝ – (2n + 1)π/2 | (-∞, -1] U [1, +∞) |
| csc θ | ℝ – nπ | (-∞, -1] U [1, +∞) |
This table provides an overview of the domain and range of common trigonometric functions. It is important to consider the specific trigonometric function and any restrictions or limitations on the input and output values when determining the domain and range.
Domain and Range of an Absolute Value Function
Absolute value functions are functions of the form f(x) = |x|, where x is the input value. The domain and range of absolute value functions depend on the specific behavior and properties of the function.
The domain of an absolute value function is all real numbers (ℝ), as it is defined for any value of x. However, the range of an absolute value function is y ≥ 0, as absolute value functions always produce non-negative values. The absolute value of any number is always positive or zero.
For example, consider the function f(x) = |x|. The domain of this function is all real numbers (ℝ), as it is defined for any value of x. The range of this function is y ≥ 0, as the absolute value of any number is always non-negative.
It is important to consider the specific behavior and properties of absolute value functions when determining their domain and range. By understanding the nature of absolute value functions, we can accurately calculate their domain and range.
Domain and Range of a Square Root Function
Square root functions are functions of the form f(x) = √x, where x is the input value. The domain and range of square root functions depend on the specific behavior and properties of the function.
The domain of a square root function is x ≥ 0, as the square root of a negative number is undefined in the real number system. Square root functions are only defined for non-negative values of x.
The range of a square root function is y ≥ 0, as the square root of any non-negative number is always non-negative. Square root functions always produce non-negative values.
For example, consider the function f(x) = √x. The domain of this function is x ≥ 0, as the square root of a negative number is undefined. The range of this function is y ≥ 0, as the square root of any non-negative number is always non-negative.
It is important to consider the specific behavior and properties of square root functions when determining their domain and range. By understanding the nature of square root functions, we can accurately calculate their domain and range.
Domain and Range of a Rational Function
Rational functions are functions that involve ratios of two polynomials. The domain and range of rational functions depend on the specific behavior and properties of the function.
The domain of a rational function is determined by the values of x for which the denominator is not equal to zero. Division by zero is undefined, so we need to avoid those values. The domain can be found by setting the denominator of the function not equal to zero and solving for x.
The range of a rational function can vary depending on the specific function. It is determined by the behavior of the function as x approaches positive or negative infinity. The range can be found by analyzing the end behavior of the function and identifying any horizontal asymptotes.
For example, consider the function f(x) = 1 / (x – 1). To find the domain of this function, we need to set the denominator not equal to zero: x – 1 ≠ 0. Solving this inequality, we find x ≠ 1. Therefore, the domain of the function f(x) = 1 / (x – 1) is all real numbers except x = 1.
The range of a rational function can be found by analyzing the end behavior and identifying any horizontal asymptotes. In this case, as x approaches positive or negative infinity, the function approaches zero. Therefore, the range of the function f(x) = 1 / (x – 1) is y ≠ 0.
By understanding the behavior and properties of rational functions, we can accurately determine their domain and range.
Domain and Range From Graph
One way to find the domain and range of a function is by looking at its graph. The domain of a function is the set of all x-values that appear on the graph, while the range is the set of all y-values that appear on the graph. To find these values, you look at the horizontal and vertical extents of the graph.
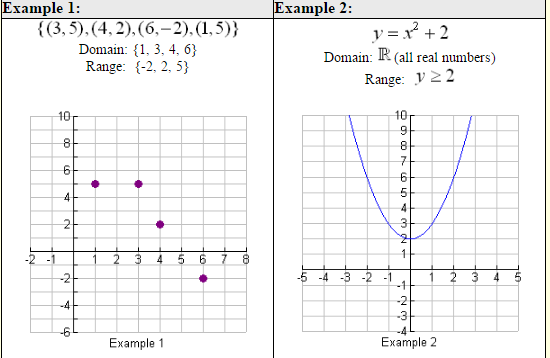
Interval Notation of Domain and Range
Interval notation is a way of writing subsets of the real number line. It uses brackets to indicate whether endpoints are included in the interval. For example, the interval [a, b] means all the numbers between a and b, including a and b. The interval (a, b) means all the numbers between a and b, excluding a and b. This notation is often used to express the domain and range of a function.
Quadratic Domain and Range
A quadratic function is a function of the form y = ax² + bx + c, where a, b, and c are constants. The domain of a quadratic function is all real numbers, because you can substitute any real number for x and compute a real number for y. The range of a quadratic function, however, depends on the leading coefficient a. If a is positive, then the range is all numbers greater than or equal to the minimum value of the function. If a is negative, then the range is all numbers less than or equal to the maximum value of the function.
Solved Examples on Domain and Range
Let’s take a look at some examples to further illustrate how to find the domain and range of different types of functions.
Example 1: Find the domain and range of the following function: f(x)=5x+3
Solution: Any real number, negative, positive or zero can be replaced with x in the given function. Therefore, the domain of the function f(x)=5x+3 is all real numbers, or as written in interval notation, is: D:(−∞,∞)). Because the function f(x)=5x+3 is a polynomial of degree 1, it is a straight line (without any breaks or holes).
The range of any polynomial of degree 1 is all real numbers or written in interval notation, is: R: (−∞,∞).
Example 2: Find the range of the function f(x) = 1/ (4x − 3).
Solution: Let the function be f(x) = y = 1/ (4x − 3)
y(4x − 3) = 1
4xy – 3y = 1
4xy = 1 + 3y
x = 4y / (1 + 3y)
Here, we observe that x is defined for all the values except of y for y = −1/3 as on y = -1/3, we get an undefined value of x.
So, the range of f(x) = 1/ (4x − 3) is (−∞, −1/3) U (1/3, ∞)
Example 3: Find the domain of f(x) = 1/(x2 – 1)
Solution: Given,
- f(x) = 1/(x2 – 1)
Now, putting x = -1, 1 in f(x)
- f(-1) = 1/{(-1)2 – 1} = 1/0 = ∞
- f(1) = 1/{(1)2 – 1} = 1/0 = ∞
Thus, on -1 and 1 the function is f(x) is undefined and apart form that at all points the f(x) is defined. Thus, the domain of f(x) is R – {-1, 1}
How Kunduz Can Help You Learn Domain and Range?
Kunduz is a powerful tool that can help you master the concepts of domain and range, as well as many other math topics. With Kunduz, you can access a wide range of resources and tools, including step-by-step solutions, expert guidance, and interactive learning experiences. Kunduz is designed to help you learn at your own pace and in your own way, making it a valuable companion on your journey to math mastery.
