Entropy is a fundamental concept in the field of thermodynamics, which is the study of energy and its transformations. It is a measure of the randomness or disorder in a system. The concept of entropy was first introduced by the German physicist Rudolf Clausius in the 19th century. Since then, it has become a central concept in the understanding of the behavior of matter and energy.
What is Entropy?
Entropy can be understood as a measure of the number of possible arrangements or configurations of a system. The greater the number of arrangements, the higher the entropy. In other words, entropy is a measure of the system’s disorder or randomness.
Entropy is often described in terms of the probability or likelihood of a particular arrangement occurring in a system. A highly ordered or organized system has low entropy, while a highly disordered or random system has high entropy.

Entropy: The Second Law of Thermodynamics
The concept of entropy is closely related to the second law of thermodynamics, which states that the entropy of an isolated system always increases over time. This means that natural processes tend to move towards a state of greater disorder or randomness.
The second law of thermodynamics can be understood in terms of the statistical behavior of particles. In any given system, there are many more possible arrangements that correspond to high entropy than there are arrangements that correspond to low entropy. Therefore, it is much more likely for a system to move towards a higher entropy state than towards a lower entropy state.
What is Internal Energy? The Relationship between Internal Energy and Entropy
Internal energy is a measure of the total energy of a system, including both its kinetic energy (associated with motion) and its potential energy (associated with forces between particles). The internal energy of a system can change due to heat transfer, work done on or by the system, or changes in its composition.
The relationship between internal energy and entropy can be understood in terms of the second law of thermodynamics. According to the second law, the entropy of an isolated system always increases over time. This means that in any spontaneous process, the total entropy of the system and its surroundings always increases.
What is Thermodynamics?
Thermodynamics is the branch of physics that deals with the relationships between heat and other forms of energy. It is concerned with the behavior of macroscopic systems, such as gases, liquids, and solids, and how they respond to changes in temperature, pressure, and volume.
Entropy Formula
The entropy change for a process can be calculated using the formula ΔS = q_rev/T, where ΔS is the change in entropy, q_rev is the heat absorbed or released reversibly by the system, and T is the absolute temperature. This formula applies to a reversible process, which is a process that can be reversed without leaving any net effect on either the system or the surroundings.
Entropy Equation
The entropy equation related to the Second Law of Thermodynamics is ΔS_universe = ΔS_system + ΔS_surroundings. This equation states that the total change in entropy of the universe is the sum of the changes in entropy of the system and its surroundings.
How To Calculate Entropy
Calculating entropy involves several steps. Here is a step-by-step guide on how to calculate entropy:
Step 1: Determine the system and its surroundings.
Step 2: Identify the heat transfer involved in the process.
Step 3: Determine the temperature at which the heat transfer occurs.
Step 4: Calculate the entropy change using the equation ΔS = q/T.
Step 5: Consider the sign of the entropy change. A positive value indicates an increase in entropy, while a negative value indicates a decrease in entropy.
Step 6: Repeat the calculations for each relevant heat transfer in the process.
Step 7: Sum up the entropy changes to find the total entropy change for the system.
Entropy Symbol
The symbol used to represent entropy is S.
Entropy Diagram
An entropy diagram is a graphical representation of the entropy of a substance as a function of temperature. It shows how the entropy changes with temperature and can provide valuable information about the behavior of the substance.

Units of Entropy
The SI unit for entropy is joules per kelvin (J/K).
Entropy Change
Entropy change refers to the difference in entropy between two states of a system. It is a measure of how much the randomness or disorder of the system has changed.
Reversible and Irreversible Changes
In thermodynamics, a reversible process is one that can be reversed by an infinitesimal change in the conditions of the system, while an irreversible process is one that cannot be reversed by such a change. Reversible processes are idealized and do not occur in practice, while irreversible processes are common in the real world.
Properties of Entropy
Entropy has several important properties:
- Entropy is a state function, which means that it depends only on the state of the system and not on the path taken to reach that state.
- Entropy is an extensive property, which means that it depends on the size or amount of the system.
- Entropy is always positive or zero. It can never be negative.
- The entropy of a system increases with an increase in temperature.
- The entropy of a system increases with an increase in the number of microstates.
Standard Entropy
Standard entropy is the entropy of a substance at a standard state, which is defined as a pressure of 1 bar and a temperature of 298 K. It is denoted by the symbol S°.
Entropy Change of Reaction
The entropy change of a reaction is a measure of the change in entropy that occurs when a reaction takes place. It is calculated by subtracting the sum of the entropies of the reactants from the sum of the entropies of the products.
Entropy and Feasible Reactions
Entropy plays a crucial role in determining the feasibility of a reaction. In general, a reaction is more likely to be spontaneous if it results in an increase in entropy. This is because an increase in entropy corresponds to a greater number of possible arrangements or configurations, which makes the reaction more likely to occur.
Development of Entropy Concept
The concept of entropy has evolved over time, beginning with the work of Rudolf Clausius in the 19th century. Clausius introduced the concept of entropy as a measure of the disorder or randomness in a system. Since then, the concept has been further developed and refined by many other scientists.
Applications of Entropy
Entropy has numerous applications in various fields. Some of the key applications include:
- Thermodynamics: Entropy is a fundamental concept in thermodynamics and is used to describe the behavior of energy and matter in systems.
- Information theory: Entropy is used to measure the amount of information in a message or signal.
- Statistical mechanics: Entropy is used to describe the behavior of systems with a large number of particles.
- Economics: Entropy is used to model and analyze economic systems, such as market dynamics and resource allocation.
- Biology: Entropy is used to study biological systems, such as protein folding and gene regulation.
State Variables and Functions of State
Entropy is a state variable, which means that it depends only on the current state of the system and not on how the system reached that state. It is also a function of state, which means that it can be determined by the values of other state variables, such as temperature and pressure.
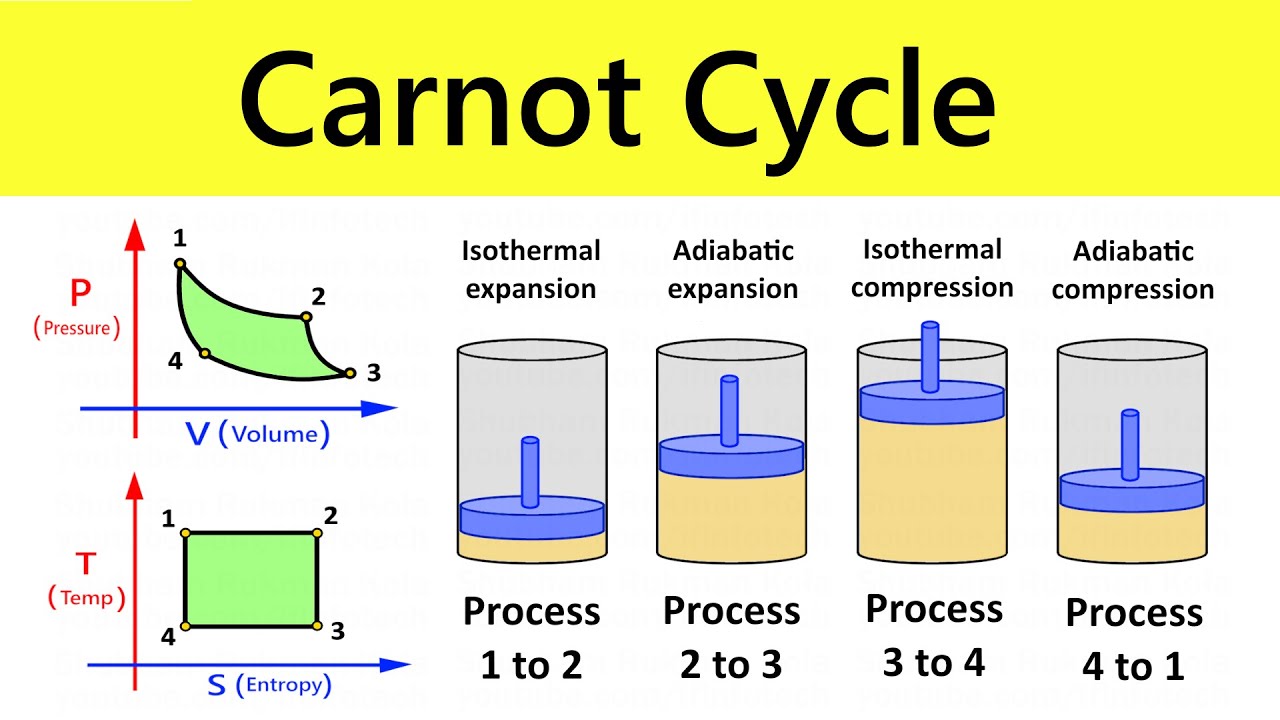
Carnot Cycle
The Carnot cycle is a theoretical thermodynamic cycle that represents the most efficient possible heat engine. It consists of four reversible processes: isothermal expansion, adiabatic expansion, isothermal compression, and adiabatic compression.
Classical Thermodynamics
Classical thermodynamics is the branch of thermodynamics that deals with macroscopic systems and their behavior. It is based on a set of fundamental principles and laws, including the first and second laws of thermodynamics.
Statistical Mechanics
Statistical mechanics is the branch of physics that connects the microscopic behavior of individual particles to the macroscopic behavior of systems. It provides a statistical description of systems with a large number of particles, such as gases and liquids.
Entropy of a System
The entropy of a system is a measure of the number of possible arrangements or configurations of the system. It is related to the probability or likelihood of a particular arrangement occurring.
Equivalence of Definitions
There are several different ways to define entropy, but they are all equivalent. This means that they all give the same value for entropy in a given system.
Difference Between Entropy and Enthalpy
| Entropy | Enthalpy |
|---|---|
| Represents disorder or randomness in a system | Represents the heat content of a system |
| Denoted by ‘S’ | Denoted by ‘H’ |
| Unit: Joules per Kelvin (J/K) | Unit: Joules (J) |
| Calculated using the formula: ΔS = q_rev/T | Calculated using the formula: ΔH = q_p (at constant pressure) |
Solved Examples on Entropy
Example 1: Calculate the entropy change when 100 J of heat is transferred to a system at 300 K.
Solution: The entropy change can be calculated using the formula ΔS = q/T.
ΔS = 100 J / 300 K = 0.33 J/K
Therefore, the entropy change is 0.33 J/K.
Example 2: Calculate the entropy change when 1 mol of gas expands against a constant pressure of 1 atm.
Solution: The entropy change can be calculated using the formula ΔS = nR ln(V2/V1), where n is the number of moles of gas, R is the gas constant, and V2/V1 is the ratio of the final and initial volumes.
Assuming an ideal gas, n = 1 mol, R = 8.314 J/(mol K), V2/V1 = 2.
ΔS = (1 mol)(8.314 J/(mol K)) ln(2) = 5.76 J/K
Therefore, the entropy change is 5.76 J/K.
Example 3: Calculate the change in entropy when 2 mol of a substance melts at its melting point of 100°C. The heat of fusion is 10 kJ/mol.
Solution: The change in entropy can be calculated using the formula ΔS = ΔHfusion/T, where ΔHfusion is the heat of fusion and T is the temperature in Kelvin.
Assuming the substance is an ideal solid, ΔHfusion = 10 kJ/mol and T = 100 + 273 = 373 K.
ΔS = (10 kJ/mol)/(373 K) = 26.8 J/(mol K)
Therefore, the change in entropy is 26.8 J/(mol K).
How Kunduz Can Help You Learn Entropy?
At Kunduz, we understand the importance of mastering concepts like entropy in the field of thermodynamics. That’s why we offer a range of resources and learning materials to help you understand and apply this fundamental concept.
Whether you’re a student studying thermodynamics for the first time or a professional looking to deepen your understanding of entropy, Kunduz is here to support you. Our user-friendly platform and accessible learning materials make it easy to learn and master this important concept.
Don’t let entropy intimidate you. With Kunduz, you can confidently navigate the complexities of thermodynamics and unlock new opportunities for learning and growth. Join us today and take your understanding of entropy to the next level.
