The circle is a fundamental concept in geometry, and it plays a crucial role in various mathematical problems and real-world applications. The equation of a circle is an algebraic expression that provides a concise way to describe a circle’s geometric properties on a coordinate plane.
An Introduction to the Equation of Circle
A circle is a two-dimensional geometric shape defined by a set of points in a plane that are equidistant from a fixed point, called the center. This distance from the center to any point on the circle is known as the radius. When we plot a circle on a coordinate plane, we typically need to know the coordinates of the center and the length of the radius.
What is an Equation of Circle?
In mathematics, the equation of a circle is an algebraic representation that defines the position of all points on the circle within a Cartesian plane. This equation is particularly useful in coordinate geometry and can be represented in various forms, including general form, standard form, parametric form, and polar form.
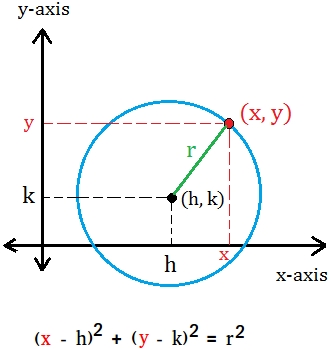
Equation of Circle Formula
The equation of a circle, in its most common or standard form, is given by:
[ (x – h)² + (y – k)² = r² ]
Here, (h, k) represents the coordinates of the center of the circle, and r represents the radius of the circle. Additionally, (x, y) denotes an arbitrary point on the circumference of the circle.
Derivation of Circle Equation
The equation of a circle can be derived from the distance formula. Given that (h, k) is the center of the circle and r is the radius, any point (x, y) on the circle’s circumference is at a distance equal to the radius from the center. Applying the distance formula, we have:
[ √{(x – h)² + (y – k)²} = r ]
Squaring both sides, we get the standard form of the equation of the circle:
[ (x – h)² + (y – k)² = r² ]
Graphing the Equation of Circle
To graph the equation of a circle on a coordinate plane, we need to know the center’s coordinates and the radius length. Once we have these details, we can plot the center on the plane, use the radius to determine the boundary points, and then draw the circle. For example, suppose we have a circle with the equation (x – 3)² + (y – 2)² = 36. The center of this circle would be at (3, 2), and its radius would be 6 units.

How to Find the Equation of a Circle?
Finding the equation of a circle involves knowing the coordinates of the center and the length of the radius. Depending on the location of the center, there are several scenarios we might face.
Equation of Circle With Center at (x1, y1)
When the center of the circle is at any general point (x1, y1), and the radius is r, the equation of the circle is given as:
[ (x – x1)² + (y – y1)² = r² ]
Equation of Circle With Center at the Origin
If the circle’s center is at the origin (0, 0), its equation simplifies to:
[ x² + y² = r² ]
Equation of Circle With Centre on x-Axis
When the center of the circle is on the x-axis at a point (a, 0), the equation of the circle becomes:
[ (x – a)² + y² = r² ]
Equation of Circle With Centre on Y-Axis
When the center of a circle is on the y-axis at a point (0, b), the equation of the circle becomes:
[ x² + (y – b)² = r² ]
Equation of Circle Touching x-Axis
If a circle touches the x-axis, the y-coordinate of its center is equal to the radius (r), and its equation becomes:
[ (x – a)² + (y – r)² = r² ]
Equation of Circle Touching y-Axis
If a circle touches the y-axis, the x-coordinate of the center equals the radius (r), and its equation becomes:
[ (x – r)² + (y – b)² = r² ]
Equation of Circle Which Touches Both the Axes
If a circle touches both axes, the coordinates of the center of the circle become equal to the radius (r, r), and its equation becomes:
[ (x – r)² + (y – r)² = r² ]
Different Forms of Equation of Circle
Depending on the parameters known, the equation of a circle can be expressed in several forms, including the general form, standard form, parametric form, and polar form.
General Equation of a Circle
The general form of the equation of a circle is written as:
[ x² + y² + 2gx + 2fy + c = 0 ]
In this form, (x, y) is any point on the circle, and g, f, and c are constants. This form is useful for finding the center and radius of a circle.
Standard Equation of a Circle
The standard form of the equation of a circle is the most common representation and is given as:
[ (x – h)² + (y – k)² = r² ]
Here, (h, k) represents the coordinates of the center of the circle, and r represents the radius of the circle.
Parametric Equation of a Circle
The parametric equation of a circle introduces a new variable, usually denoted as θ, which represents an angle. The parametric equations are given as:
[ x = h + rcos(θ), y = k + rsin(θ) ]
Polar Equation of a Circle
The polar form of the equation of a circle is written as:
[ r = a ]
Here, a is the radius of the circle, and r, θ are the polar coordinates. This form is particularly useful when the circle is centered at the origin.
Converting General Form to Standard Form
To convert the general form of the equation of a circle to the standard form, we complete the square for the x and y terms. Here’s how:
Given a general form equation of a circle as:
[ x² + y² + 2gx + 2fy + c = 0 ]
We rearrange the equation to group the x terms and y terms together:
[ x² + 2gx + y² + 2fy = -c ]
Then, we complete the square for the x terms and the y terms:
[ (x² + 2gx + g²) – g² + (y² + 2fy + f²) – f² = – c ]
This simplifies to:
[ (x + g)² + (y + f)² = g² + f² – c ]
Which matches the standard form of the equation of a circle:
[ (x – h)² + (y – k)² = r² ]
Converting Standard Form to General Form
To convert the standard form of the equation of a circle to the general form, we expand the squares and simplifying the equation. Here’s how:
Given a standard form equation of a circle as:
[ (x – h)² + (y – k)² = r² ]
We expand the squares:
[ (x² – 2hx + h²) + (y² – 2ky + k²) = r² ]
Then, we rearrange the equation to group the x terms and y terms together:
[ x² – 2hx + y² – 2ky + (h² + k² – r²) = 0 ]
This matches the general form of the equation of a circle:
[ x² + y² + 2gx + 2fy + c = 0 ]
How Kunduz Can Help You Learn the Equation of Circle?
Kunduz is an innovative learning platform that provides expert assistance in understanding the equation of a circle and other geometry concepts. Its user-friendly interface and interactive learning materials make studying fun and effective. With Kunduz, students can access comprehensive resources such as detailed explanations, step-by-step solutions, and interactive quizzes to reinforce their understanding of the equation of a circle and other complex mathematical concepts.
