An equilateral triangle is a fundamental geometric shape that has fascinated mathematicians for centuries. With its three equal sides and three equal angles, the equilateral triangle is a symmetrical and balanced figure. In this article, we will explore the definition, properties, angles, area, formulas, and examples related to the equilateral triangle.
An Introduction to the Equilateral Triangle
The equilateral triangle is a type of triangle where all three sides are of equal length. This means that each angle of the equilateral triangle measures 60 degrees. The term “equilateral” is derived from the Latin words “aequus,” meaning equal, and “latus,” meaning side. Therefore, an equilateral triangle can also be referred to as a regular triangle.
What is an Equilateral Triangle?
An equilateral triangle is a polygon with three congruent sides and three congruent angles. It is considered a regular polygon because all its sides and angles are equal. The sides of an equilateral triangle are denoted by the length “a.” In an equilateral triangle, all three sides measure “a,” and all three angles measure 60 degrees.
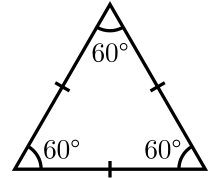
Properties of Equilateral Triangle
The equilateral triangle possesses several unique properties that distinguish it from other types of triangles. These properties include:
- Equal Side Lengths: All three sides of an equilateral triangle are equal in length. In triangle ABC, sides AB = BC = CA = a units.
- Equal Angles: All three angles of an equilateral triangle are equal to 60 degrees. In triangle ABC, ∠A = ∠B = ∠C = 60°.
- Symmetry: The equilateral triangle has three lines of symmetry, dividing the triangle into three congruent parts.
- Perpendicular Bisector: The perpendicular drawn from any vertex of an equilateral triangle to the opposite side bisects the side and the vertex angle, creating two equal halves.
- Orthocenter and Centroid: The orthocenter and centroid of an equilateral triangle coincide at the same point.
- Equal Medians, Angle Bisectors, and Altitudes: The medians, angle bisectors, and altitudes of an equilateral triangle for all sides are equal.
Angles of Equilateral Triangle
The angles of an equilateral triangle are all congruent and measure 60 degrees. Each angle is formed by the intersection of two sides of the triangle. The sum of the interior angles of any triangle is always 180 degrees, so in an equilateral triangle, 60 + 60 + 60 = 180 degrees.
Shape of Equilateral Triangle
The shape of an equilateral triangle resembles a regular polygon with three sides. It is a closed figure with straight sides and three vertices. The equilateral triangle is the simplest regular polygon and is widely observed in our surroundings. Some examples of equilateral triangle shapes include tiles, clocks, nachos, and sweets.
Equilateral Triangle Formulas
To calculate various aspects of an equilateral triangle, we can use specific formulas. These formulas include:
Area of an Equilateral Triangle
The area of an equilateral triangle can be calculated using the formula:
Area of an Equilateral Triangle = √3/4 * a²
where “a” represents the side length of the triangle.
Perimeter of an Equilateral Triangle
The perimeter of an equilateral triangle is equal to the sum of all three side lengths. Since all three sides are equal, the perimeter can be calculated using the formula:
Perimeter of an Equilateral Triangle = 3 * a
where “a” represents the side length of the triangle.
Height of an Equilateral Triangle
The height or altitude of an equilateral triangle can be determined using the formula:
Height of an Equilateral Triangle = √3/2 * a
where “a” represents the side length of the triangle.
Equilateral Triangle Area using Heron’s Formula
Heron’s formula is a method to calculate the area of a triangle when only the lengths of the sides are known. For an equilateral triangle, the formula becomes:
Area of an Equilateral Triangle = √3/4 * a²
where “a” represents the side length of the triangle.
Derivation for Equilateral Triangle Formula
The formula for the area of an equilateral triangle can be derived using basic trigonometry. Consider an equilateral triangle with side length “a.” If we draw an altitude from one vertex to the opposite side, it will divide the equilateral triangle into two congruent right-angled triangles.
By using the Pythagorean theorem, we can find the height of the equilateral triangle. The hypotenuse of one of the right-angled triangles is “a,” and one of the legs is “a/2.” Let’s denote the height as “h.” Applying the Pythagorean theorem, we have:
(h)² + (a/2)² = a²
Simplifying the equation, we get:
h² + a²/4 = a²
Multiplying both sides by 4, we have:
4h² + a² = 4a²
Rearranging the equation, we get:
4h² = 3a²
Taking the square root of both sides, we have:
2h = √3a
Dividing both sides by 2, we get:
h = √3/2 * a
Therefore, the formula for the area of an equilateral triangle is:
Area of an Equilateral Triangle = √3/4 * a²
Equilateral Triangle Theorem And Proof
The equilateral triangle theorem states that for any equilateral triangle ABC, if P is any point on the arc BC of the circumcircle of triangle ABC, then PA = PB + PC. This theorem can be proved using the properties of an equilateral triangle.
To prove the theorem, consider an equilateral triangle ABC with a circumcircle. Let P be any point on the arc BC of the circumcircle. We can prove that PA = PB + PC by using the properties of cyclic quadrilaterals and the angle sum property of triangles.
Let’s consider the cyclic quadrilateral ABPC. By the properties of cyclic quadrilaterals, we know that the opposite angles of a cyclic quadrilateral add up to 180 degrees. Therefore, we have:
∠PAB + ∠PBC = 180° ∠PAC + ∠PCB = 180°
Since triangle ABC is an equilateral triangle, all angles are equal to 60 degrees. Let’s denote the measure of ∠PAB = ∠PAC = ∠PBC = x. Substituting these values into the equations, we get:
x + 60° = 180° x + 60° = 180°
Simplifying the equations, we have:
x = 120°
Therefore, all three angles of the cyclic quadrilateral ABPC are equal to 120 degrees. Now, let’s consider triangle PAB. Since PB = PA, we can denote their length as “y.” By the angle sum property of triangles, we have:
x + 60° + 60° = 180°
Simplifying the equation, we get:
x = 60°
Therefore, the measure of angle ∠PAB = 60 degrees. By the properties of equilateral triangles, we know that ∠PAB = ∠PBC = ∠PCB = 60 degrees.
Now, let’s consider the equation PA = PB + PC. Since PB = PA = y, we can rewrite the equation as:
y = y + PC
Simplifying the equation, we get:
PC = 0
Therefore, PC is equal to zero, which means that point P coincides with point C. Hence, the equilateral triangle theorem is proved.
Centroid of Equilateral Triangle
The centroid of a triangle is the point of concurrency of all three medians. In an equilateral triangle, the centroid coincides with the orthocenter and circumcenter. This point divides each median into two segments, with the distance from the centroid to the vertex being twice the distance from the centroid to the midpoint of the opposite side.
The coordinates of the centroid of an equilateral triangle with side length “a” are given by:
Centroid (x, y) = (0, a/√3)

Differences between Scalene Triangles, Isosceles Triangles, and Equilateral Triangles (Table)
Let’s compare the differences between scalene triangles, isosceles triangles, and equilateral triangles in a table format:
| Property | Scalene Triangle | Isosceles Triangle | Equilateral Triangle |
|---|---|---|---|
| Side Lengths | All sides have different lengths. | Two sides have the same length, and one side is different. | All sides have the same length. |
| Angle Measures | All angles have different measures. | Two angles have the same measure, and one angle is different. | All angles have the same measure (60 degrees). |
| Lines of Symmetry | No lines of symmetry. | One line of symmetry (axis of symmetry through the equal sides). | Three lines of symmetry (axis of symmetry through each side and through each angle bisector). |
| Congruent Segments | No congruent segments. | Two congruent segments (the equal sides). | Three congruent segments (all sides). |
| Altitudes | Altitudes are of different lengths. | Altitudes from the equal sides are of the same length, and the altitude from the unequal side is a different length. | All altitudes are of the same length. |
| Perpendicular Bisects | Perpendicular bisects are of different lengths. | Perpendicular bisects from the equal sides are of the same length, and the perpendicular bisect from the unequal side is different. | Perpendicular bisects are of the same length. |
| Circumcircle Center | No specific relationship between the center of the circumcircle and the triangle. | The center of the circumcircle lies on the perpendicular bisect of the unequal side. | The center of the circumcircle coincides with the centroid and orthocenter of the triangle. |
| Area Formula | No specific formula due to varying side lengths. | Area = 1/2 * base * height (base is the unequal side and height is the perpendicular from the base to the opposite vertex). | Area = √3/4 * a² (a is the side length). |
| Perimeter Formula | No specific formula due to varying side lengths. | Perimeter = 2 * equal side length + unequal side length. | Perimeter = 3 * side length. |
| Examples | Triangle with side lengths 3 cm, 4 cm, and 5 cm. | Triangle with side lengths 4 cm, 4 cm, and 6 cm. | Triangle with side lengths 5 cm, 5 cm, and 5 cm. |
| Classification | Scalene triangle. | Isosceles triangle. | Equilateral triangle. |
Frequently Asked Questions About Equilateral Triangle
Let’s address some frequently asked questions related to the equilateral triangle:
Does an equilateral triangle have a 180-degree angle?
No, an equilateral triangle does not have a 180-degree angle. Each angle in an equilateral triangle measures 60 degrees. The sum of the interior angles of any triangle is always 180 degrees.
Do equilateral triangles have equal sides and angles?
Yes, equilateral triangles have equal sides and angles. All three sides of an equilateral triangle are equal in length, and all three angles are equal, measuring 60 degrees.
What is the Equilateral Triangle Altitude Formula?
The formula to calculate the altitude of an equilateral triangle is:
Height of an Equilateral Triangle = √3/2 * a
where “a” represents the side length of the triangle.
Is the Equilateral Triangle a Regular Polygon?
Yes, an equilateral triangle is considered a regular polygon. A regular polygon is a polygon with all sides and angles equal. Since an equilateral triangle has equal sides and angles, it meets the criteria for a regular polygon.
How many Sides and Angles does an Equilateral Triangle have?
An equilateral triangle has three sides and three angles. The lengths of all three sides are equal, and all three angles measure 60 degrees.
Solved Examples on Equilateral Triangle
Let’s solve some examples related to the equilateral triangle to further understand its properties and formulas.
Example 1: Finding the Area of an Equilateral Triangle
Find the area of an equilateral triangle when the side length is 6 cm.
Solution: Given data: Side length (a) = 6 cm
We know that the formula for the area of an equilateral triangle is:
Area of an Equilateral Triangle = √3/4 * a²
Substituting the given values into the formula, we have:
Area = √3/4 * (6)² = √3/4 * 36 = 9√3 cm²
Therefore, the area of the equilateral triangle is 9√3 square cm.
Example 2: Finding the Perimeter of an Equilateral Triangle
Find the perimeter of an equilateral triangle when the side length is 10 cm.
Solution: Given data: Side length (a) = 10 cm
We know that the formula for the perimeter of an equilateral triangle is:
Perimeter of an Equilateral Triangle = 3 * a
Substituting the given values into the formula, we have:
Perimeter = 3 * 10 = 30 cm
Therefore, the perimeter of the equilateral triangle is 30 cm.
Example 3: Finding the Height of an Equilateral Triangle
Find the height of an equilateral triangle with a side length of 8 cm.
Solution: Given data: Side length (a) = 8 cm
We know that the formula for the height of an equilateral triangle is:
Height of an Equilateral Triangle = √3/2 * a
Substituting the given values into the formula, we have:
Height = √3/2 * 8 = 4√3 cm
Therefore, the height of the equilateral triangle is 4√3 cm.
How Kunduz Can Help You Learn Equilateral Triangle?
At Kunduz, we understand the importance of mastering geometry concepts like the equilateral triangle. We offer a range of resources, including online tutorials, interactive lessons, and practice problems, to help you enhance your understanding of this topic. Our step-by-step explanations and visual aids make learning geometry enjoyable and accessible. Whether you’re a student looking to improve your grades or an educator seeking additional teaching materials, Kunduz is here to support your learning journey. Join us today and unlock the world of geometry with ease.
