Fractions are a fundamental aspect of mathematics, representing parts of a whole or a collection. Each fraction consists of two parts: the numerator (the number above the line) and the denominator (the number below the line). The numerator indicates how many equal parts of the whole are taken, while the denominator shows how many equal parts the whole has been divided into.
Equivalent fractions, a crucial concept within the realm of fractions, are fractions that may appear different due to their distinct numerators and denominators but actually represent the same value. To put it simply, they are ‘equal in value but different in appearance’.
What are Equivalent Fractions?
As the name suggests, equivalent fractions are fractions that are equivalent or equal in value, even though their numerators (top number) and denominators (bottom number) may differ. To illustrate, the fractions 1/2, 2/4, and 3/6 are all equivalent fractions, as they all represent the same value or proportion of a whole, despite comprising different numerators and denominators.
In essence, equivalent fractions highlight the phenomenon that different fractions can represent the same mathematical value or ratio.

How to Find Equivalent Fractions?
Identifying equivalent fractions involves two primary methods:
Multiplying the Numerator and Denominator by the Same Number
To discover equivalent fractions, you can multiply both the numerator and the denominator of the given fraction by the same number. This method is based on the principle that multiplying by 1 (which is what you’re doing when you multiply the numerator and the denominator by the same value) does not alter the original value of the fraction.
For instance, to find an equivalent fraction for 3/4, you can multiply the numerator (3) and the denominator (4) by the same number, say, 2. Hence, 6/8 is an equivalent fraction of 3/4.
Dividing the Numerator and Denominator by the Same Number
Equally, you can generate equivalent fractions by dividing both the numerator and denominator of the given fraction by the same number. This process, often referred to as simplifying fractions, is particularly useful for finding the simplest form of a fraction.
For example, to find an equivalent fraction for 18/24, you can divide both the numerator (18) and the denominator (24) by their common factor, which is 6. Hence, 3/4 is an equivalent fraction of 18/24.
Equivalent Fractions Chart
A chart or table can be an invaluable tool to visualize and comprehend equivalent fractions. Here’s an example of an equivalent fractions chart:
| Unit Fraction | Equivalent Fractions |
|---|---|
| 1/2 | 2/4, 3/6, 4/8… |
| 1/3 | 2/6, 3/9, 4/12… |
| 1/4 | 2/8, 3/12, 4/16… |
| 1/5 | 2/10, 3/15, 4/20… |
| 1/6 | 2/12, 3/18, 4/24… |
| 1/7 | 2/14, 3/21, 4/28… |
| 1/8 | 2/16, 3/24, 4/32… |
| 1/9 | 2/18, 3/27, 4/36… |
This chart provides the equivalent fractions for various unit fractions (fractions with a numerator of 1). It serves as a quick reference tool to understand and identify equivalent fractions.
Methods to Determine Equivalent Fractions
There are several methods to determine whether two fractions are equivalent:
- Making the Denominators the Same: By finding the Least Common Multiple (LCM) of the denominators and adjusting the fractions accordingly, you can check if they are equivalent.
- Finding the Decimal Form for Both the Fractions: Converting both fractions to decimal form can help determine their equivalence. If the decimal forms are identical, the fractions are equivalent.
- Cross Multiplication Method: Cross multiplying the numerators and denominators of two fractions and comparing the products can indicate equivalence. If both products are the same, the fractions are equivalent.
- Visual Method: Drawing pictures or using physical objects to represent the fractions can provide a visual confirmation of equivalence.
How to Create Equivalent Fractions?
Creating equivalent fractions involves either multiplying or dividing both the numerator and denominator of the given fraction by the same number. This process is based on the principle of maintaining the value of the fraction, as multiplying or dividing by the same number is akin to multiplying or dividing by 1, which does not alter the original value.
For instance, to generate equivalent fractions for 2/3, you can multiply or divide both the numerator and denominator by the same number, say 2. Consequently, 4/6 (obtained by multiplying) and 1/1.5 (obtained by dividing) are equivalent fractions for 2/3.
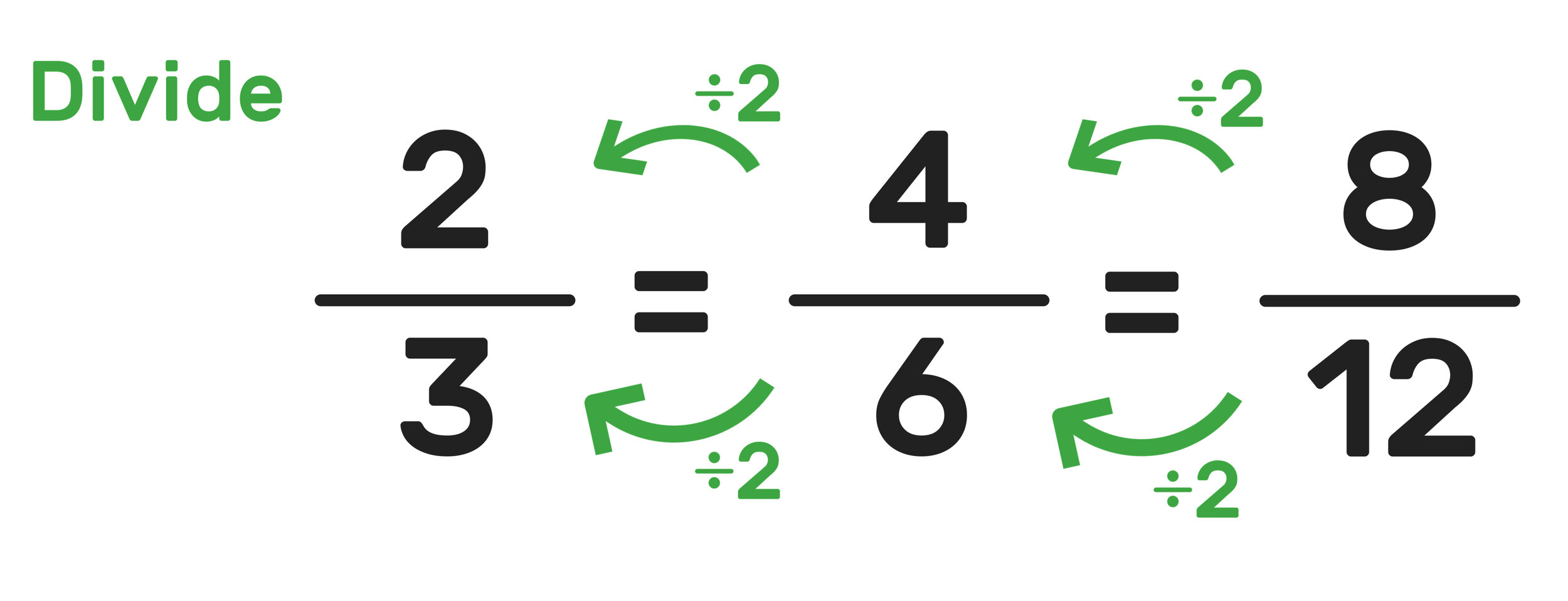
How to Order Fractions with Different Denominators
Ordering fractions with different denominators can be a challenging task. However, understanding the concept of equivalent fractions can simplify this process. To order fractions with different denominators, you first need to convert them into equivalent fractions with the same denominator (preferably the Least Common Multiple or LCM of the original denominators). Once the fractions have the same denominator, you can easily order them based on their numerators.
How do you know if Two Fractions are Equivalent?
There are various methods to determine whether two fractions are equivalent:
Making the Denominators the Same
By making the denominators the same (via finding the LCM of the denominators and modifying the fractions accordingly), you can check if the fractions are equivalent. If both fractions are equivalent to the same fraction with the LCM as the denominator, they are equivalent.
Finding the Decimal form of Both the Fractions
By converting both fractions into decimal form and comparing the results, you can ascertain their equivalence. If both fractions yield the same decimal, they are equivalent.
Cross Multiplication Method
The cross multiplication method involves cross multiplying the numerators and denominators of the two fractions and comparing the products. If both products are equal, the fractions are equivalent.
Visual Method
The visual method involves representing each fraction pictorially or graphically on identical shapes and checking if the shaded portions of both shapes are equal. If they are, the fractions are equivalent.
Equivalent Fractions Examples
Let’s consider some examples of equivalent fractions:
- 1/2, 2/4, and 3/6: All these fractions are equivalent as they represent the same value – half of the whole.
- 2/3, 4/6, and 6/9: These fractions are equivalent as they all equate to two-thirds of the whole.
- 3/4, 6/8, and 9/12: These fractions are equivalent as they all represent three-fourths of the whole.
Solved Examples on Equivalent Fractions
Example 1: Find an equivalent fraction for 2/3 by multiplying the numerator and denominator by 4.
Solution: 2/3 * 4/4 = 8/12 Thus, the equivalent fraction for 2/3 is 8/12.
Example 2: Find an equivalent fraction for 5/6 by dividing the numerator and denominator by 2.
Solution: 5/6 ÷ 2/2 = 5/6 ÷ 2/2 = 5/6 ÷ 1 = 5/6 Thus, the equivalent fraction for 5/6 is 5/6.
Example 3: Determine if 3/4 and 6/8 are equivalent fractions.
Solution: To check if two fractions are equivalent, we can simplify both fractions to their simplest form. 3/4 = 3 * 1/4 * 1 = 3/4 6/8 = 6 * 1/8 * 1 = 6/8 Since both fractions are already in their simplest form and have the same value, 3/4 and 6/8 are equivalent fractions.
How Kunduz Can Help You Learn Equivalent Fractions?
Understanding the concept of equivalent fractions is crucial for developing solid mathematical foundations. At Kunduz, we offer personalized one-on-one math tutoring programs for grades 2 through 8, aligned with your state’s standards and assessments.
Our experienced and dedicated online math tutors provide differentiated instruction to close individual learning gaps and ensure every student learns at the right pace. Plus, we provide regular reports every step of the way, so you can track your progress.
For those grasping the concept of equivalent fractions and keen on furthering their understanding of fraction operations, our subtracting fractions and division of fractions pages serve as valuable companions. These resources delve into essential principles that enhance the comprehension of fraction manipulation, providing a well-rounded exploration of mathematical operations within the realm of fractions.
