Exponential functions play a crucial role in mathematics and have numerous real-world applications. They help us understand exponential growth and decay, model populations, compute investments, and more. In this comprehensive guide, we will explore the definition, formula, properties, graphs, rules, asymptotes, domain, and range of exponential functions. So let’s dive in and unravel the fascinating world of exponential functions!
An Introduction to Exponential Functions
Exponential functions are mathematical functions that involve exponents. They are characterized by the form f(x) = ax, where “x” is a variable and “a” is a constant known as the base of the function. The base “a” should be greater than 0 and not equal to 1. The most commonly used base for exponential functions is the transcendental number e, which is approximately equal to 2.71828.
What are Exponential Functions?
Exponential functions are functions that grow or decay at a constant rate. The growth or decay is determined by the base “a” in the function. If the base “a” is greater than 1, the function exhibits exponential growth. On the other hand, if the base “a” is between 0 and 1, the function shows exponential decay. Exponential functions are widely used in various fields, such as biology, finance, physics, and more, to model natural phenomena.
What is Exponential Growth And Decay?
Exponential growth and decay are fundamental concepts associated with exponential functions. Exponential growth refers to a situation where a quantity increases rapidly over time. It starts slowly and then accelerates at an ever-increasing rate. On the other hand, exponential decay occurs when a quantity decreases rapidly over time. It starts with a high value and then gradually approaches zero.
Exponential Function Formula
The formula for an exponential function is f(x) = ax, where “a” is the base of the function and “x” is the exponent. The base “a” can be any positive number greater than 0. The value of the exponent “x” determines the growth or decay of the function. If “x” is positive, the function experiences exponential growth. If “x” is negative, the function undergoes exponential decay.
Exponential Growth
Exponential growth can be represented by the formula y = a(1 + r)^x, where “a” is the initial value, “r” is the growth rate, and “x” is the time. The growth rate “r” is expressed as a decimal or fraction. The exponential growth formula is commonly used in population studies, compound interest calculations, and other scenarios where quantities grow rapidly.
Exponential Decay
Exponential decay can be represented by the formula y = a(1 – r)^x, where “a” is the initial value, “r” is the decay rate, and “x” is the time. The decay rate “r” is expressed as a decimal or fraction. The exponential decay formula is used in scenarios where quantities decrease rapidly over time, such as radioactive decay or the depreciation of assets.
| Exponential Growth | Exponential Decay |
|---|---|
| The function increases rapidly and then more rapidly over time. | The function decreases rapidly and then more slowly over time. |
| Represented by y = a(1 + r)^x. | Represented by y = a(1 – r)^x. |
| Used to model population growth, compound interest, etc. | Used to model radioactive decay, depreciation of assets, etc. |
Exponential Function Graph
Graphing exponential functions helps visualize their behavior and understand their properties. The graph of an exponential function depends on the base “a” and the exponent “x”. Let’s take a look at the graph of the exponential function y = 2^x.

From the graph, we can observe that the exponential function y = 2^x is an increasing function. It starts at (0, 1) and grows rapidly as x increases. The graph never intersects the x-axis and approaches it asymptotically as x approaches negative infinity. The exponential function graph exhibits exponential growth.
Now, let’s consider the graph of the exponential function y = (1/2)^x.
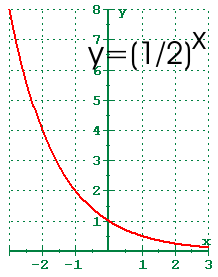
In this case, the exponential function y = (1/2)^x is a decreasing function. It starts at (0, 1) and decreases as x increases. The graph never intersects the x-axis and approaches it asymptotically as x approaches positive infinity. The exponential function graph demonstrates exponential decay.
Exponential Function Equation
The exponential function equation is given by f(x) = ax, where “a” is the base and “x” is the exponent. The equation represents the relationship between the input variable “x” and the output variable “f(x)” in the exponential function. By manipulating the equation, we can solve for different variables and explore various properties of exponential functions.
Exponential Function Derivative
The derivative of an exponential function is equal to the function itself. In other words, the rate of change of an exponential function at any point is proportional to its current value. The unique property of exponential functions is that their derivatives are equal to the original functions. For example, the derivative of f(x) = e^x is f'(x) = e^x.
The Natural Exponential Function
The natural exponential function is a specific type of exponential function with the base “e”. The constant “e” is a transcendental number approximately equal to 2.71828. The natural exponential function is denoted by f(x) = e^x. It plays a significant role in various areas of mathematics, science, and engineering due to its unique properties and applications.
Exponential Series
The exponential function can be represented as a power series, allowing it to be extended to complex numbers. The power series representation of the exponential function is given by:
e^x = 1 + x + (x^2 / 2!) + (x^3 / 3!) + …
This power series converges for all real and complex values of “x”. It provides an alternative way to define the exponential function and allows for calculations involving complex numbers and infinite series expansions.
Parameters of the Exponential Function
The exponential function has several important parameters that affect its behavior. These parameters include the base “a”, the exponent “x”, the initial value, growth rate, and decay rate. Understanding these parameters is crucial for interpreting and manipulating exponential functions in various contexts.
Exponential Function Properties
Exponential functions exhibit several unique properties that distinguish them from other types of functions:
- The domain of an exponential function is all real numbers, while the range is all positive real numbers.
- The graph of an exponential function is always above the x-axis.
- The function is always increasing if the base is greater than one and decreasing if the base is less than one.
- The graph passes through the point (0, 1), irrespective of the base.
Exponential Function Rules
Exponential functions follow specific rules, often referred to as the laws of exponents. These rules include:
- a^x × a^y = a^(x + y)
- a^x / a^y = a^(x – y)
- (a^x)^y = a^(xy)
- a^-x = 1 / a^x
- a^0 = 1
Exponential Function Asymptotes
Asymptotes are horizontal, vertical, or oblique lines that a function approaches but never intersects. Exponential functions have a horizontal asymptote at y = 0. This means that as x approaches positive or negative infinity, the graph of the exponential function gets arbitrarily close to the x-axis but never touches it. The presence of asymptotes helps us understand the long-term behavior of exponential functions.
Domain and Range of Exponential Function
The domain of an exponential function is the set of all real numbers, as exponential functions are defined for any real input. However, the range of an exponential function depends on the base “a”. If the base “a” is greater than 1, the range includes all positive real numbers. If the base “a” is between 0 and 1, the range includes all positive real numbers less than 1. Understanding the domain and range of exponential functions is crucial for interpreting their graphs and solving equations involving exponential functions.
Integration of Exponential Function
The integration of exponential functions involves finding the antiderivative of the function. The antiderivative of an exponential function f(x) = ax is given by F(x) = (a^x) / ln(a), where ln(a) is the natural logarithm of the base “a”. This integration formula allows us to calculate the area under the curve of an exponential function and solve problems involving exponential growth or decay.
Frequently Asked Questions on Exponential Functions
How do you know if a function is exponential?
A function is considered exponential if it can be written in the form f(x) = ax, where “a” is a constant and “x” is the variable. The variable “x” appears as an exponent in the function. Exponential functions exhibit specific growth or decay patterns depending on the base “a”.
How do you write an exponential function?
To write an exponential function, you need to determine the base “a” and the exponent “x” that represent the relationship between the input and output variables. The base “a” determines the growth or decay rate, while the exponent “x” represents the variable being raised to a power. The general form of an exponential function is f(x) = ax.
How does exponential growth compare to polynomial growth?
Exponential growth and polynomial growth are distinct mathematical concepts. Exponential growth refers to a situation where a quantity increases rapidly over time, while polynomial growth refers to a situation where a quantity increases at a slower rate over time. Exponential growth is characterized by an exponential function, while polynomial growth is characterized by a polynomial function.
How do you Simplify an Exponential Equation?
To simplify an exponential equation, you can apply the rules of exponents. These rules include combining like terms, factoring out common factors, and simplifying expressions with exponents. By simplifying an exponential equation, you can make it easier to solve and understand.
How do you Solve an Exponential Equation Using a Log?
To solve an exponential equation using a logarithm, you can take the logarithm of both sides of the equation. This allows you to bring down the exponent and solve for the variable. By using logarithms, you can easily solve exponential equations and find the value of the variable that satisfies the equation.
What are the different types of exponential functions?
There are various types of exponential functions, depending on the base “a”. Some common types include exponential growth functions, exponential decay functions, and natural exponential functions. The type of exponential function depends on the value of the base and its effect on the growth or decay of the function.
Solved Examples on Exponential Functions
Let’s solve a couple of examples to demonstrate how exponential functions can be applied in real-world situations.
Example 1: Population Growth
The population of a city is currently 100,000 and is growing at an annual rate of 5%. Write an exponential function to model the population growth over time.
Solution:
The exponential function can be written as P(t) = P0 * (1 + r)^t, where P(t) is the population at time t, P0 is the initial population, r is the growth rate, and t is the time.
In this case, P0 = 100,000, r = 0.05 (5%), and t is the number of years.
The exponential function for population growth is P(t) = 100,000 * (1 + 0.05)^t.
Example 2: Compound Interest
You invest $10,000 in a savings account that offers an annual interest rate of 3%. Write an exponential function to model the growth of your investment over time.
Solution:
The exponential function can be written as A(t) = P * (1 + r/n)^(n*t), where A(t) is the amount at time t, P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the time in years.
In this case, P = $10,000, r = 0.03 (3%), n = 1 (compounded annually), and t is the number of years.
The exponential function for compound interest is A(t) = $10,000 * (1 + 0.03/1)^(1*t).
Example 3: Solve for x in the given equation: 2^(2x) = 16.
Solution: Given equation: 2^(2x) = 16 Rewrite 16 as a power of 2: 2^(2x) = 2^4 Now, as the bases are equal, equate the powers: 2x = 4 Solving for x gives us: x = 4/2 = 2
Therefore, the solution to the given equation is x = 2.
How Kunduz Can Help You Learn Exponential Functions?
At Kunduz, we understand the importance of mastering exponential functions for academic success. We offer a comprehensive range of resources, including online tutorials, practice questions, and personalized guidance, to help you grasp the concepts and excel in your studies.
Our experienced teachers and academic experts are dedicated to providing clear and concise explanations, step-by-step solutions, and practical examples to ensure your understanding of exponential functions. With Kunduz, you can learn at your own pace, ask questions, and gain the confidence to tackle any problem involving exponential functions.
