Mathematics is a fascinating subject that encompasses a wide range of concepts and patterns. One such pattern that has captivated mathematicians for centuries is the Fibonacci sequence. Named after the Italian mathematician Leonardo Fibonacci, this sequence has a unique set of properties and is found in various natural and man-made phenomena. In this article, we will explore the formula, spiral, properties, list, formulas, golden ratio, diagrams, and examples associated with the Fibonacci sequence.
What is Fibonacci Sequence?
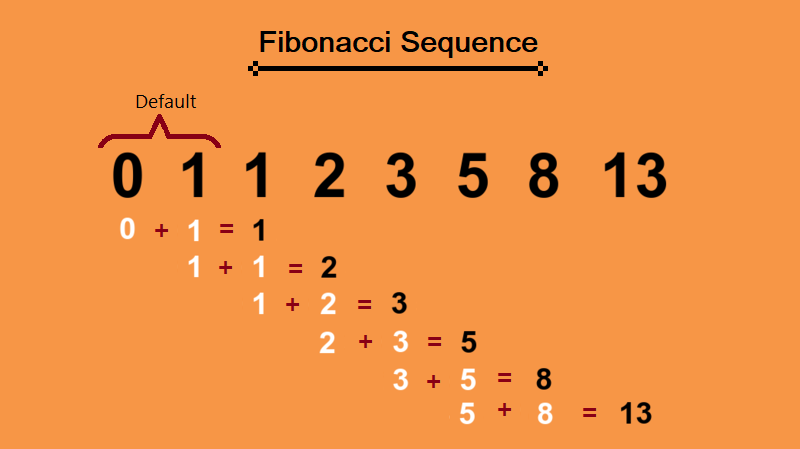
The Fibonacci sequence is a series of numbers in which each number is the sum of the two preceding numbers. It starts with 0 and 1, and the subsequent numbers are obtained by adding the two preceding numbers. The sequence continues infinitely and is denoted by the symbol “Fn.” The first few numbers of the Fibonacci sequence are as follows:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
As the sequence progresses, the ratio between consecutive Fibonacci numbers approaches a constant value known as the Golden Ratio, which is approximately 1.61803. This ratio has been observed in various natural and man-made structures, leading to its significance in mathematics and aesthetics.
Who is Leonardo Fibonacci?
Leonardo Fibonacci, also known as Leonardo of Pisa, was an Italian mathematician born in the 12th century. He introduced the Fibonacci sequence to the Western world through his book “Liber Abaci” (Book of Calculation) in 1202. Fibonacci encountered the sequence while studying the breeding patterns of rabbits, which led him to discover its mathematical properties. His work revolutionized mathematics and introduced Hindu-Arabic numerals to Europe, making him one of the most influential mathematicians of the Middle Ages.
:max_bytes(150000):strip_icc()/Leonardo-Pisano-Fibonacci-f9d544e22fb147fea36f99b4dcd77f50.jpg)
Fibonacci Spiral
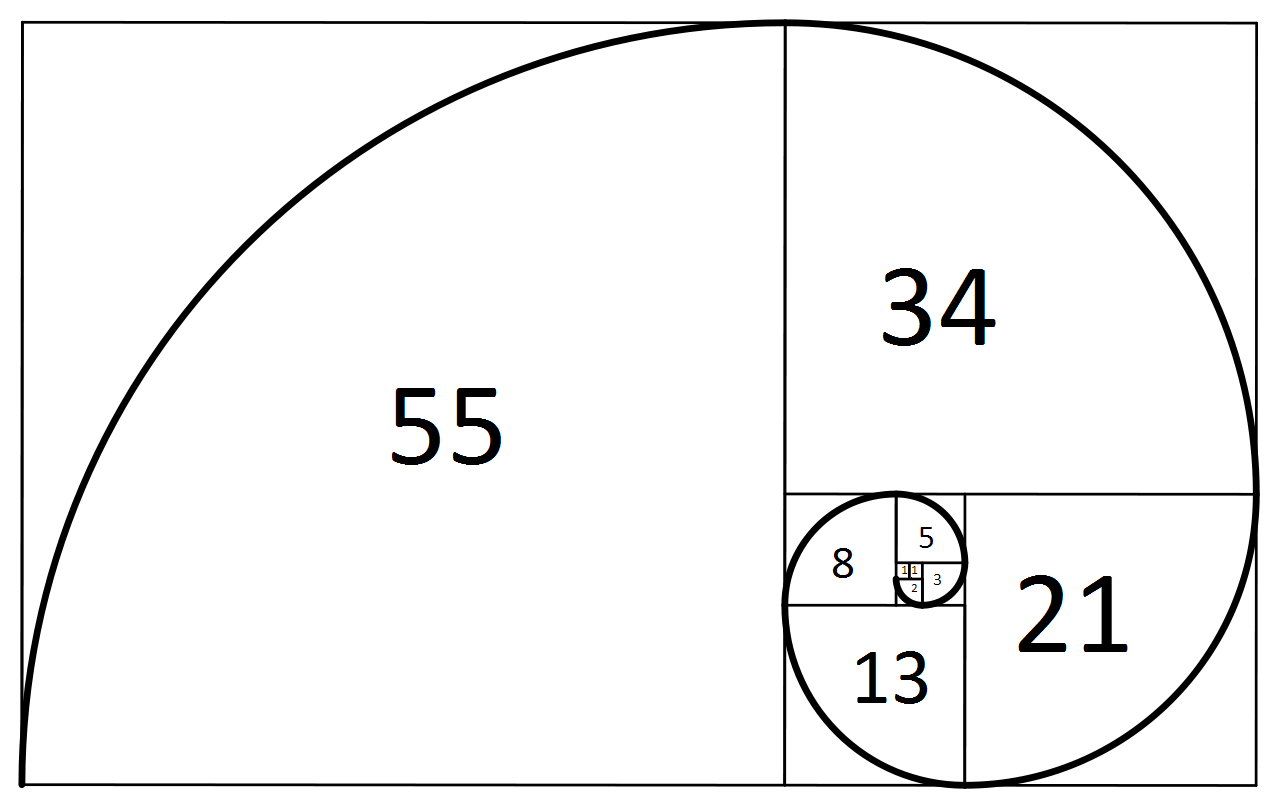
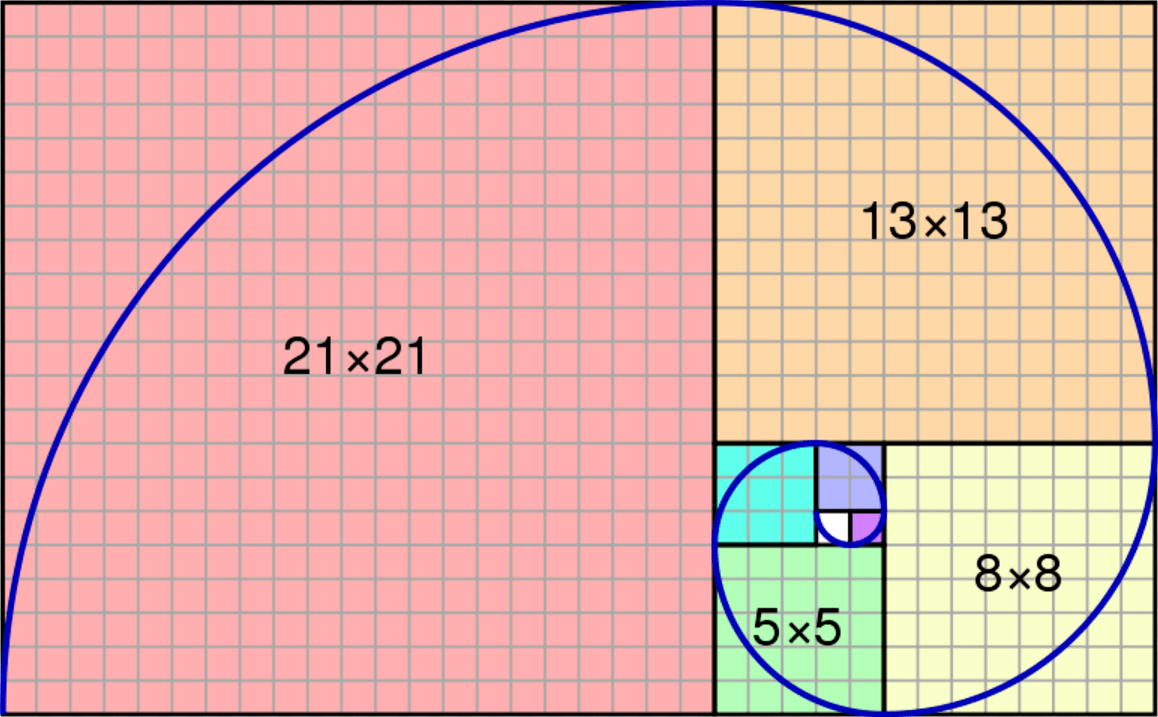
One of the fascinating aspects of the Fibonacci sequence is its connection to the Fibonacci spiral. The spiral is formed by drawing arcs connecting the corners of squares with side lengths equal to Fibonacci numbers. Starting with a small square, each subsequent square is added in a clockwise direction, creating a spiral pattern. This spiral can be observed in various natural phenomena, such as the arrangement of seeds in a sunflower, the shape of a nautilus shell, and the branching of trees.
Fibonacci Sequence Formula
The Fibonacci sequence can be expressed using a formula. The formula for calculating the nth term of the Fibonacci sequence is as follows:
Fn = Fn-1 + Fn-2
This means that each number in the sequence is obtained by adding the two preceding numbers. For example, to find the 6th term of the sequence, we add the 5th and 4th terms: 3 + 2 = 5. Similarly, to find the 7th term, we add the 6th and 5th terms: 5 + 3 = 8.
Fibonacci Sequence List
The Fibonacci sequence is an infinite sequence, but we can generate a list of Fibonacci numbers up to a certain term. Here is a table showing the Fibonacci sequence up to the 10th term:
| Term Position | Fn Term | Term Value / Fibonacci number |
|---|---|---|
| 1st | F0 | 0 |
| 2nd | F1 | 1 |
| 3rd | F2 | 1 |
| 4th | F3 | 2 |
| 5th | F4 | 3 |
| 6th | F5 | 5 |
| 7th | F6 | 8 |
| 8th | F7 | 13 |
| 9th | F8 | 21 |
| 10th | F9 | 34 |
Properties of Fibonacci Sequence
The Fibonacci sequence exhibits several interesting properties that make it a subject of fascination for mathematicians. Some of these properties include:
- Every third number in the sequence, starting at 2, is a multiple of 2. Similarly, every fourth number after 3 is a multiple of 3, every fifth number after 5 is a multiple of 5, and so on.
- The sum of two odd numbers is always an even number, whereas the sum of an even and an odd number is an odd number. Thus, the Fibonacci sequence follows an even, odd, odd, even, odd, odd pattern.
- The ratio between consecutive Fibonacci numbers approaches the Golden Ratio, which is approximately 1.61803. This ratio has aesthetic significance and can be found in various natural and man-made structures.
Golden Ratio to Calculate Fibonacci Numbers
The Golden Ratio, also known as phi (Φ), is a mathematical constant that has a close connection to the Fibonacci sequence. It is obtained by dividing a Fibonacci number by its preceding number as the sequence approaches infinity. The value of the Golden Ratio is approximately 1.61803. This ratio has been used in art, architecture, and design to create aesthetically pleasing proportions and compositions. The Golden Ratio can be calculated using the following formula:
ϕ = (1 + √5) / 2

History of Fibonacci Sequence
The Fibonacci sequence has a rich history that dates back to ancient civilizations. While Leonardo Fibonacci introduced the sequence to the Western world in the 12th century, its origins can be traced back to ancient Indian mathematics. The sequence was later studied by various mathematicians, including Indian mathematicians such as Pingala and Gopala, who discovered similar sequences in Sanskrit poetry. The Fibonacci sequence gained popularity in Europe during the Renaissance period and has since been a subject of fascination for mathematicians and scientists.
Calculating the Fibonacci Sequence
To calculate the Fibonacci sequence, we start with the first two terms, 0 and 1. Each subsequent term is obtained by adding the two preceding terms. Let’s calculate the Fibonacci sequence up to the 10th term:
Step 1: Start with the first two terms: 0, 1.
Step 2: Add the preceding two terms to get the next term.
- 0 + 1 = 1
Step 3: Add the last two terms to get the next term.
- 1 + 1 = 2
Step 4: Continue this process until we reach the desired term.
- 1 + 2 = 3
- 2 + 3 = 5
- 3 + 5 = 8
- 5 + 8 = 13
- 8 + 13 = 21
- 13 + 21 = 34
| Term | Fn Value |
|---|---|
| 1st | 0 |
| 2nd | 1 |
| 3rd | 1 |
| 4th | 2 |
| 5th | 3 |
| 6th | 5 |
| 7th | 8 |
| 8th | 13 |
| 9th | 21 |
| 10th | 34 |
Importance of Fibonacci Sequence
The Fibonacci sequence holds great importance in mathematics and various other fields. It serves as a foundation for understanding number patterns, ratios, and proportions. The sequence has applications in algebra, number theory, geometry, and computer science. It is also utilized in financial markets for technical analysis and predicting price movements. Moreover, the Fibonacci sequence and its properties have inspired artists, architects, and designers to create aesthetically pleasing compositions and structures.
Recursive Formula in Fibonacci Sequence
The Fibonacci sequence is a recursive sequence, meaning that each term is obtained by adding the two preceding terms. The recursive formula for the Fibonacci sequence can be expressed as follows:
Fn = Fn-1 + Fn-2
This recursive formula allows us to generate the Fibonacci sequence indefinitely by continuously adding the preceding two terms.
Types of Fibonacci Sequence
While the traditional Fibonacci sequence starts with 0 and 1, variations of the sequence can be generated by altering the initial terms. Some common types of Fibonacci sequences include the Lucas numbers, which start with 2 and 1, and the Pell numbers, which start with 0 and 1. These variations exhibit similar properties to the traditional Fibonacci sequence but have different initial terms.
Fibonacci Sequence Diagram
A diagram can be used to visualize the Fibonacci sequence and its patterns. The diagram typically consists of squares with side lengths equal to Fibonacci numbers arranged in a spiral pattern. This spiral is known as the Fibonacci spiral and can be observed in various natural phenomena, such as the arrangement of seeds in a sunflower or the shape of a nautilus shell.
Fibonacci Sequence and Binet’s Formula
Binet’s formula is an equation that allows us to calculate the nth term of the Fibonacci sequence without having to compute all the preceding terms. The formula is as follows:
F(n) = (phi^n – (-phi)^(-n)) / sqrt(5)
Here, phi represents the Golden Ratio, approximately equal to 1.61803. Using this formula, we can directly calculate any term of the Fibonacci sequence without having to go through the recursive process of summing the preceding terms.
The Sum of the Fibonacci Sequence
The sum of the Fibonacci sequence can be calculated using a formula derived from Binet’s formula. The sum of the first n terms of the Fibonacci sequence is given by:
∑(i=0 to n) Fi = F(n+2) – 1
For example, to find the sum of the first 10 terms of the Fibonacci sequence, we can use the formula: F(10+2) – 1 = F(12) – 1 = 144 – 1 = 143.
Finding Lucas Numbers from the Fibonacci Sequence
The Fibonacci sequence gives rise to another number sequence known as the Lucas numbers. The Lucas numbers start with 2 and 1, and each subsequent term is obtained by adding the two preceding terms, similar to the Fibonacci sequence. The Lucas numbers can be found within the Fibonacci sequence by skipping every other term. For example, the Lucas sequence derived from the Fibonacci sequence is as follows:
2, 1, 3, 4, 7, 11, 18, …
Fibonacci Sequence in Pascal’s Triangle
The Fibonacci sequence can also be found within Pascal’s triangle, a triangular array of numbers named after the French mathematician Blaise Pascal. In Pascal’s triangle, each number is the sum of the two numbers directly above it. If we look at the numbers on the diagonals of Pascal’s triangle, we will find the Fibonacci sequence. For example, the numbers on the diagonal of Pascal’s triangle are:
1, 1, 2, 3, 5, 8, …
Uses of the Fibonacci Sequence
The Fibonacci sequence has various applications in different fields. Some of the notable uses include:
- Coding: The Fibonacci sequence is used in coding, particularly in algorithms and distributed systems.
- Financial Analysis: The sequence is utilized in financial markets for technical analysis, predicting price movements, and determining support and resistance levels.
- Design and Architecture: The Golden Ratio, derived from the Fibonacci sequence, is used in design and architecture to create aesthetically pleasing proportions and compositions.
Applications of Fibonacci Sequence
The Fibonacci sequence finds applications in numerous fields, including:
- Art: Many artists incorporate the Fibonacci sequence and Golden Ratio in their compositions to create visually appealing artworks.
- Nature: The Fibonacci sequence appears in various natural phenomena, such as the arrangement of seeds in sunflowers, the branching of trees, and the shape of seashells.
- Biology: The sequence is observed in the growth patterns of plants, the structure of DNA molecules, and the spirals of pinecones.
- Geometry: The Fibonacci sequence is related to the geometry of shapes such as rectangles, squares, and the Golden Spiral.
Fibonacci Sequence in Nature
One of the most intriguing aspects of the Fibonacci sequence is its presence in the natural world. The sequence can be observed in various natural phenomena, including:
- Plants: The arrangement of seeds in sunflowers and pinecones follows the Fibonacci sequence. The spirals formed by these seeds exhibit the Golden Ratio.
- Animals: The breeding patterns of certain animals, such as rabbits, can be described using the Fibonacci sequence. Each pair of rabbits produces a new pair, resulting in the sequence 1, 1, 2, 3, 5, 8, …
- Shells: The spirals found in seashells, such as the nautilus shell, often conform to the Fibonacci sequence and the Golden Ratio.
- Galaxies: The spiral arms of galaxies often follow the Fibonacci sequence, providing insight into the structure and formation of these celestial bodies.
Solved Examples on Fibonacci Sequence
Let’s solve a few examples to better understand the Fibonacci sequence:
Example 1: Find the sum of the first 15 Fibonacci numbers.
Solution: Using the formula for the sum of the Fibonacci sequence, we can calculate:
∑(i=0 to 15) Fi = F(15+2) – 1 = F(17) – 1 = 1596 – 1 = 1595
Therefore, the sum of the first 15 Fibonacci numbers is 1595.
Example 2: Find the 5th Fibonacci number.
Solution: By using the formula for the nth Fibonacci number, we can calculate:
F(5) = F(5-1) + F(5-2) = F(4) + F(3) = 3 + 2 = 5
Therefore, the 5th Fibonacci number is 5.
Example 3: Find the next number when F14 = 377.
Solution: To find the next number in the sequence, we can use the Golden Ratio.
F(15) = F(14) x Golden Ratio ≈ 377 x 1.61803 ≈ 610
Therefore, the next number in the sequence is 610.
Example 4: Calculate the value of F(-6).
Solution: The Fibonacci sequence can be extended to negative indices using the formula:
F(-n) = (-1)^(n+1) x F(n)
Therefore, F(-6) = (-1)^(6+1) x F(6) = -1 x 8 = -8.
How Kunduz Can Help You Learn the Fibonacci Sequence?
At Kunduz, we understand the importance of a strong foundation in mathematics and aim to provide comprehensive learning resources to help you master concepts like the Fibonacci sequence. Our study materials, step-by-step explanations, are designed to make learning enjoyable and accessible. Whether you’re a student or an enthusiast, Kunduz is here to support your journey in understanding the fascinating world of mathematics. Join us today and unlock the potential of your mathematical abilities!
