In this article, we will explore the concept of geometric sequences, also known as geometric progressions. A geometric sequence is a series of numbers in which each term is obtained by multiplying the preceding term by a constant factor called the common ratio. We will discuss the definition, properties, and formulas related to geometric sequences, as well as provide examples and answer frequently asked questions.
An Introduction to the Geometric (Progression) Sequence?
Sequences play a crucial role in mathematics, as they help us identify patterns and relationships between numbers. A geometric sequence is a specific type of sequence where each term is obtained by multiplying the previous term by a constant ratio. This constant ratio is denoted by the letter “r” and can be either positive or negative.
Geometric sequences have various applications in different fields, such as finance, physics, and computer science. Understanding geometric sequences allows us to analyze and predict patterns in a wide range of real-world scenarios.
What is a Geometric (Progression) Sequence?
A geometric sequence is a pattern of numbers where each consecutive term is obtained by multiplying the preceding term by a constant, referred to as the common ratio. This common ratio, symbolized by ‘r’, could be positive or negative, but never zero. For instance, the sequence 2, 4, 8, 16, 32, 64, … showcases a geometric sequence where the common ratio is 2. Each successive term in this sequence is twice the preceding term.
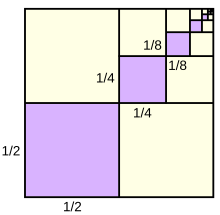
What is a Geometric Progression?
A geometric progression is another term used to describe a geometric sequence. It refers to the series of numbers obtained by following the pattern of multiplying each term by a common ratio. Geometric progressions can be either finite or infinite.
- Finite Geometric Progression: A finite geometric progression is a sequence that contains a finite number of terms. In other words, it has a defined last term. For example, the sequence 2, 6, 18, 54 is a finite geometric progression with a common ratio of 3.
- Infinite Geometric Progression: An infinite geometric progression is a sequence that continues indefinitely without a defined last term. For example, the sequence 2, 4, 8, 16, … is an infinite geometric progression with a common ratio of 2.
Geometric Sequence Formulas
nth Term of Geometric Sequence Formula
The formula for the nth term of a geometric sequence is given as an = ar^(n-1), where ‘an’ denotes the nth term, ‘a’ is the first term, and ‘r’ is the common ratio. This formula assists in finding any term in the sequence without requiring the knowledge of the preceding term.
Recursive Formula of Geometric Sequence
The recursive formula for a geometric sequence is an = r * a_(n-1), where ‘an’ is the nth term, ‘a_(n-1)’ is the preceding term, and ‘r’ is the common ratio. This formula is used when the preceding term and the common ratio are known.
Sum of Finite Geometric Sequence Formula
The sum of the first ‘n’ terms of a finite geometric sequence is given by the formula Sn = a * (r^n - 1) / (r - 1). Here, ‘Sn’ represents the sum of the first ‘n’ terms, ‘a’ is the first term, ‘r’ is the common ratio, and ‘n’ is the number of terms.
Sum of Infinite Geometric Sequence Formula
For an infinite geometric sequence, the sum is given by S = a / (1 - r), where ‘S’ is the sum, ‘a’ is the first term, and ‘r’ is the common ratio. This formula is applicable when the absolute value of the common ratio is less than 1, that is, |r| < 1.
Explicit Rule
The explicit rule for a geometric sequence is an = ar^(n-1). This rule allows us to find any term in the sequence directly without needing to find any other terms first.
General Form of Geometric Progression
The general form of a geometric progression is represented as a, ar, ar^2, ar^3, ..., ar^(n-1). Here, ‘a’ denotes the first term, ‘r’ is the common ratio, and ‘n’ is the number of terms. This form shows how each term in the sequence is generated by multiplying the preceding term by the common ratio.

Common Ratio of Geometric Progression
The common ratio of a geometric progression is the constant ratio between any term and its preceding term. It can be found by dividing any term by its preceding term. The common ratio is denoted by the letter “r”.
For example, if we have a geometric progression with terms 2, 4, 8, 16, 32, … the common ratio is 2. Each term is obtained by multiplying the preceding term by 2.
Sum of N term of Geometric Progression
The sum of the first n terms of a geometric progression can be calculated using the following formula:
Sn = a * (1 – r^n) / (1 – r)
Here, “Sn” represents the sum of the first n terms, “a” is the first term, “r” is the common ratio, and “n” is the number of terms.
This formula allows us to find the sum of a specific number of terms in a geometric progression.
Types of Geometric Sequence
Geometric sequences can be classified into two types based on the number of terms:
Finite Geometric Progression
A finite geometric progression is a sequence that has a finite number of terms. In other words, it has a defined last term. The last term of a finite geometric progression can be represented as ar^(n-1), where “a” is the first term, “r” is the common ratio, and “n” is the number of terms.
For example, the sequence 1, 2, 4, 8, 16 is a finite geometric progression with a common ratio of 2.
Infinite Geometric Progression
An infinite geometric progression is a sequence that continues indefinitely without a defined last term. The terms in an infinite geometric progression can be represented as ar^(n-1), where “a” is the first term, “r” is the common ratio, and “n” is the position of the term in the sequence.
For example, the sequence 3, 6, 12, 24, … is an infinite geometric progression with a common ratio of 2.
The distinction between finite and infinite geometric progressions lies in the number of terms in the sequence.
Properties of Geometric Sequence
Geometric sequences possess several properties that can help in understanding and analyzing their patterns. Some of these properties include:
- Multiplication Property: In a geometric sequence, each term is obtained by multiplying the preceding term by a constant ratio called the common ratio.
- Ratio Property: The ratio of any two consecutive terms in a geometric sequence is constant and equal to the common ratio (r). This means that if we divide any term by its preceding term, we will obtain the same value, which is the common ratio.
- Sum Property: The sum of the first n terms of a geometric sequence can be calculated using the formula Sn = a * (1 – r^n) / (1 – r), where “Sn” represents the sum, “a” is the first term, “r” is the common ratio, and “n” is the number of terms.
These properties allow us to identify and analyze the patterns and behavior of geometric sequences.
Geometric Sequence vs. Arithmetic Sequence
Geometric sequences are often compared to arithmetic sequences, as both involve patterns of numbers. However, there are some key differences between the two:
- Pattern: In a geometric sequence, each term is obtained by multiplying the preceding term by a constant ratio. In contrast, an arithmetic sequence involves adding a constant difference to each term to obtain the next term.
- Common Difference vs. Common Ratio: In an arithmetic sequence, the constant difference between consecutive terms is called the common difference. In a geometric sequence, the constant ratio between consecutive terms is called the common ratio.
- Growth Rate: In a geometric sequence, the terms either increase or decrease exponentially, depending on the common ratio. In an arithmetic sequence, the terms increase or decrease linearly, with a constant difference between each term.
- Applications: Geometric sequences are often used to model exponential growth or decay, such as population growth or radioactive decay. Arithmetic sequences are commonly used to model linear relationships, such as distance traveled over time or financial investments with fixed increments.
Understanding the differences between geometric and arithmetic sequences is important in various mathematical and real-world applications.
Table: Geometric Sequence vs. Arithmetic Sequence
| Property | Geometric Sequence | Arithmetic Sequence |
|---|---|---|
| Pattern | Multiplying by a common ratio | Adding a constant difference |
| Common Difference | Common Ratio | Common Difference |
| Growth Rate | Exponential | Linear |
| Applications | Exponential growth or decay | Linear relationships |
Frequently Asked Questions on Geometric Sequence
When Does a Geometric Sequence Diverge?
A geometric sequence with a common ratio ‘r’ diverges when the absolute value of ‘r’ is greater than or equal to 1, i.e., |r| ≥ 1. In such cases, the sequence does not converge to a finite value, and the sum of the sequence is undefined.
How to Find the Sum of a Finite Geometric Sequence?
The sum of the first ‘n’ terms of a finite geometric sequence can be found using the formula Sn = a * (r^n - 1) / (r - 1). Here, ‘Sn’ represents the sum of the first ‘n’ terms, ‘a’ is the first term, ‘r’ is the common ratio, and ‘n’ is the number of terms.
How to Find the Sum of an Infinite Geometric Sequence?
The sum of an infinite geometric sequence is given by the formula S = a / (1 - r), where ‘S’ is the sum, ‘a’ is the first term, and ‘r’ is the common ratio. This formula is applicable when the absolute value of the common ratio is less than 1, i.e., |r| < 1.
When Does a Geometric Sequence Converge?
A geometric sequence with a common ratio ‘r’ converges when the absolute value of ‘r’ is less than 1, i.e., |r| < 1. In such cases, the sequence converges to a finite value, and the sum of the sequence can be calculated using the formula for the sum of an infinite geometric sequence.
How to solve geometric sequences?
Geometric sequences can be solved using the geometric sequence formula an = ar^(n-1), where ‘an’ denotes the nth term, ‘a’ is the first term, and ‘r’ is the common ratio. This formula helps find any term in the sequence. To find the sum of ‘n’ terms, use the sum formula Sn = a * (r^n - 1) / (r - 1).
What is the sum of a geometric series?
The sum of a finite geometric series is given by the formula Sn = a * (r^n - 1) / (r - 1), where ‘Sn’ is the sum of ‘n’ terms, ‘a’ is the first term, ‘r’ is the common ratio, and ‘n’ is the number of terms. For an infinite geometric series where the absolute value of the common ratio is less than 1, the sum is given by S = a / (1 - r).
Solved Examples on Geometric Sequence
Let’s take a look at some solved examples to further illustrate the concepts of geometric sequences.
Example 1: Find the 10th term of the geometric sequence 1, 3, 9, 27, …
Solution: In this geometric sequence, the first term (a) is 1, and the common ratio (r) is 3. We can use the formula for the nth term of a geometric sequence to find the 10th term:
an = a * r^(n – 1)
Substituting the values, we have: a10 = 1 * 3^(10 – 1) = 1 * 3^9 = 1 * 19683 = 19683
Therefore, the 10th term of the geometric sequence is 19683.
Example 2: Find the sum of the first 15 terms of the geometric sequence 1, 1/2, 1/4, 1/8, …
Solution: In this geometric sequence, the first term (a) is 1, and the common ratio (r) is 1/2. We can use the formula for the sum of a finite geometric sequence to find the sum of the first 15 terms:
Sn = a * (1 – r^n) / (1 – r)
Substituting the values, we have: S15 = 1 * (1 – (1/2)^15) / (1 – 1/2) = 1 * (1 – 1/32768) / (1/2) = 1 * (32767/32768) / (1/2) = 2 * 32767/32768 ≈ 0.99994
Therefore, the sum of the first 15 terms of the geometric sequence is approximately 0.99994.
These examples demonstrate how to apply the formulas and concepts of geometric sequences to solve problems.
Example 3: Consider a geometric sequence where the first term ‘a’ is 2 and the common ratio ‘r’ is 3. To find the 5th term in the sequence, substitute ‘n’ as 5 in the geometric sequence formula an = ar^(n-1). Therefore, the 5th term is a5 = 2*3^(5-1) = 162.
Example 4: Let’s find the sum of the first 6 terms of a geometric sequence where the first term ‘a’ is 1 and the common ratio ‘r’ is 2. Using the sum formula Sn = a * (r^n - 1) / (r - 1), the sum of the first 6 terms is S6 = 1 * (2^6 - 1) / (2 - 1) = 63.
How Can Kunduz Help You Learn Geometric Sequence?
At Kunduz, we understand the importance of a strong foundation in mathematics. Geometric sequences are an essential topic in the study of sequences and series. We provide comprehensive study materials, practice questions, and video lessons that cover all aspects of geometric sequences.
Our step-by-step explanations and interactive learning resources make it easy for students to grasp the concepts and apply them to various problem-solving scenarios. Whether you need help understanding the formulas, finding the sum of a sequence, or solving a specific problem, Kunduz is here to support your learning journey.
By leveraging our resources, you can enhance your understanding of geometric sequences and build a solid mathematical foundation.
