In the field of mathematics, the concept of the Greatest Common Divisor (GCD) plays a crucial role. It is a fundamental concept that helps us understand the relationship between numbers and their factors. The GCD is the largest positive integer that divides two or more given numbers without leaving a remainder. It is also known as the greatest common factor (GCF) or highest common factor (HCF).
Understanding the GCD is essential in various mathematical applications, such as simplifying fractions, finding common denominators, and solving algebraic equations. In this article, we will delve into the definition of the GCD, explore different methods to find it, and provide practical examples to enhance your understanding.
For readers exploring the concept of greatest common divisors and interested in broadening their mathematical knowledge, our pages on how to rationalize the denominator and scale factor serve as valuable references. These resources offer insights into diverse mathematical techniques, providing a comprehensive exploration beyond the realm of greatest common divisors.
What is the Greatest Common Divisor?
The Greatest Common Divisor (GCD) refers to the largest positive integer that divides two or more numbers without leaving a remainder. It represents the highest common factor shared by the given numbers. For example, the GCD of 8 and 12 is 4, as 4 is the largest number that divides both 8 and 12 without a remainder.
The GCD is denoted as gcd(a, b), where ‘a’ and ‘b’ represent the given numbers. It is important to note that the GCD is always a positive integer and is never negative or zero. The GCD of any two numbers is at least 1, as the smallest common divisor is always 1.
Greatest Common Divisor Formula
The GCD of two numbers (a, b) can be calculated using the following formula:
GCD(a, b) = (a * b) / LCM(a, b)
Here, LCM refers to the Least Common Multiple of the two numbers.
Methods to Find the Greatest Common Divisor
There are several methods to find the Greatest Common Divisor (GCD) of two or more numbers. Let’s explore some of the commonly used methods:
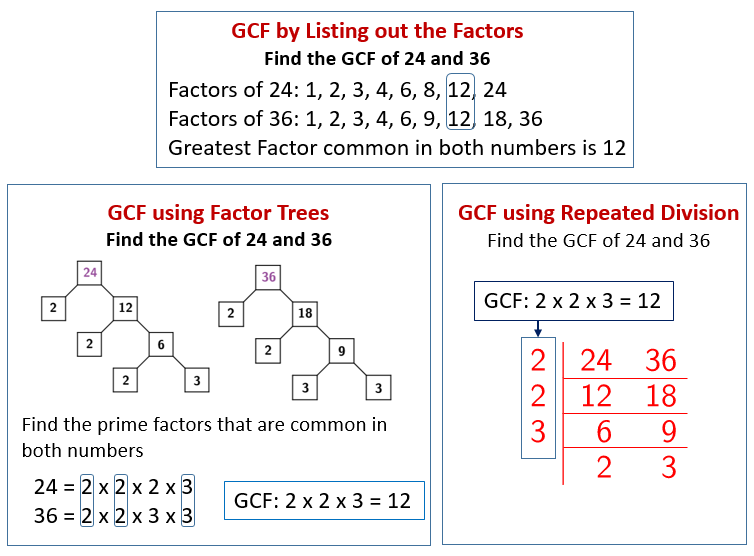
Listing Method
The listing method involves listing all the factors of the given numbers and identifying the common factors. The greatest common divisor is the largest number that appears in the list of common factors.
Repeated Division Method
The repeated division method, also known as the Euclidean algorithm, involves repeatedly dividing the larger number by the smaller number until the remainder becomes zero. The last non-zero remainder obtained is the GCD of the given numbers.
Prime Factorization Method
The prime factorization method involves finding the prime factors of the given numbers and identifying the common prime factors. The GCD is obtained by multiplying the common prime factors.
Long Division Method
The long division method is another approach to find the GCD. It involves performing long division between the given numbers and finding the remainder at each step. The GCD is the last non-zero remainder obtained.
Euclid’s Division Algorithm
Euclid’s division algorithm is an efficient method to find the GCD of two numbers. It involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder obtained. This process continues until the remainder becomes zero. The GCD is the last non-zero remainder obtained.
Each of these methods has its advantages and can be used depending on the situation and the numbers involved.
How to Find the GCD of Two Numbers?
To find the GCD of two numbers using the listing method, follow these steps:
- Write down the factors of each number.
- Identify the common factors.
- Choose the greatest common factor as the GCD.
For example, let’s find the GCD of 24 and 36 using the listing method:
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24 Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Common factors: 1, 2, 3, 4, 6, 12
GCD(24, 36) = 12
Finding Greatest Common Divisor by LCM Method
The GCD can also be found using the LCM (Least Common Multiple) method. The steps to calculate the GCD of (a, b) using the LCM method are as follows:
- Find the product of a and b.
- Find the LCM of a and b.
- Divide the product of the numbers by the LCM.
- The obtained value after division is the GCD of (a, b).
For example, let’s find the GCD of 12 and 18 using the LCM method:
Product of 12 and 18 = 216 LCM of 12 and 18 = 36
GCD(12, 18) = 216 / 36 = 6
What are Factors?
Factors are numbers that divide another number evenly without leaving a remainder. In other words, factors are the numbers that can be multiplied together to obtain a given number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
What are Common Factors?
Common factors are the factors that are shared by two or more numbers. To find the common factors of two numbers, list the factors of each number and identify the factors that appear in both lists. The common factors are the numbers that divide both numbers evenly without leaving a remainder.
For example, let’s find the common factors of 14 and 21:
Factors of 14: 1, 2, 7, 14 Factors of 21: 1, 3, 7, 21
Common factors: 1, 7
Greatest Common Factor vs. Greatest Common Divisor
The terms Greatest Common Factor (GCF) and Greatest Common Divisor (GCD) are often used interchangeably and refer to the same concept. Both terms denote the largest positive integer that divides two or more given numbers without leaving a remainder.
Applications of Greatest Common Divisor
The concept of the Greatest Common Divisor (GCD) has various practical applications in mathematics and beyond. Some of the key applications include:
- Simplifying Fractions: The GCD is used to simplify fractions by dividing both the numerator and denominator by their GCD. This process reduces fractions to their lowest terms.
- Finding Common Denominators: When adding or subtracting fractions with different denominators, the GCD is used to find the least common multiple (LCM) of the denominators, which serves as the common denominator.
- Solving Diophantine Equations: Diophantine equations are algebraic equations that require integer solutions. The GCD is used to find the solutions to these equations by applying the Extended Euclidean Algorithm.
- Cryptography: In cryptography, the GCD is used in various algorithms to ensure the security and efficiency of encryption and decryption processes.
These are just a few examples highlighting the significance of the GCD in mathematical computations and real-world applications.
Solved Examples on Greatest Common Divisor
Let’s work through some examples to illustrate how to find the Greatest Common Divisor (GCD) using different methods:
- Find the GCD of 24 and 36 using the prime factorization method.
Solution: The prime factorization of 24 is 2^3 * 3, and the prime factorization of 36 is 2^2 * 3^2. The common prime factors are 2^2 * 3, which gives the GCD as 12. - Calculate the GCD of 48 and 60 using the repeated division method.
Solution: The repeated division process yields the following steps: 48 = 2 * 24 + 0 24 = 2 * 12 + 0 12 = 2 * 6 + 0 6 = 2 * 3 + 0The GCD of 48 and 60 is 6. - Determine the GCD of 42, 56, and 70 using the long division method.
Solution: Perform long division as follows: GCD(42, 56) = 14 GCD(14, 70) = 14The GCD of 42, 56, and 70 is 14.
These examples demonstrate the different methods to find the GCD and showcase the versatility of these methods in solving various problems.
How Kunduz Can Help You Learn Greatest Common Divisor?
At Kunduz, we understand the importance of mastering mathematical concepts such as the Greatest Common Divisor (GCD). That’s why we provide comprehensive resources and personalized tutoring to help you enhance your understanding and excel in your math journey.
Our expert tutors are experienced in teaching complex mathematical concepts in a simplified and engaging manner. They can guide you through various methods to find the GCD, provide step-by-step explanations, and solve practice problems to reinforce your learning.
Whether you need assistance with finding the GCD of two numbers or understanding its applications in real-world scenarios, Kunduz is here to support you every step of the way. Our mission is to empower you with the knowledge and skills to tackle any math problem with confidence.
Don’t let math be a hurdle in your academic journey. Join Kunduz today and unlock your full mathematical potential!
