An Introduction to Henderson-Hasselbalch Equation
In the field of chemistry and biochemistry, the Henderson-Hasselbalch equation plays a crucial role in estimating the pH of buffer solutions. Buffer solutions are designed to resist changes in pH when small amounts of acid or base are added. The Henderson-Hasselbalch equation provides a relationship between the pH, the acid dissociation constant (pKa), and the molar concentrations of weak acids and their conjugate bases. By understanding this equation, we can effectively calculate and control the pH of buffer solutions.
For those exploring the concept of Henderson-Hasselbalch Equation and interested in delving deeper into various chemistry topics, our ideal gas constant and benzoic acid pages serve as valuable references. They offer insights into fundamental principles such as gas behavior and acid-base properties, complementing the understanding of Henderson-Hasselbalch Equation within the broader context of chemistry.
What is Henderson-Hasselbalch Equation?
The Henderson-Hasselbalch equation is an important tool in understanding the pH of buffer solutions. It is written as:
pH = pKa + log10 ([A–]/[HA])
In this equation, [A–] represents the molar concentration of the conjugate base, and [HA] represents the molar concentration of the weak acid. The pKa value is the negative logarithm of the acid dissociation constant (Ka) and provides information about the acid’s strength. By using the Henderson-Hasselbalch equation, we can estimate the pH of a buffer solution when the concentrations of the acid and its conjugate base are known.
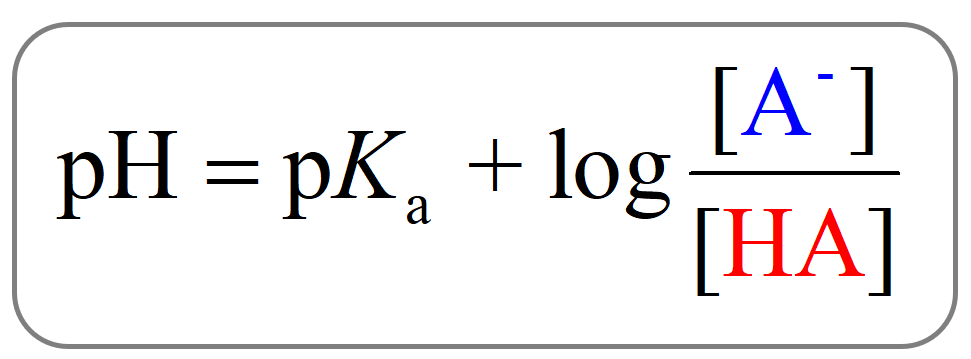
Who is Karl Albert Hasselbalch?
Karl Albert Hasselbalch, a Danish chemist, made significant contributions to the field of chemistry during the early 20th century. He is best known for re-expressing the equation derived by Lawrence Joseph Henderson in logarithmic terms. By doing so, he provided a more convenient and understandable form of the equation, which is now known as the Henderson-Hasselbalch equation. Hasselbalch’s work greatly influenced the field of acid-base chemistry and remains a fundamental concept in the study of buffer solutions.

Who is Lawrence Joseph Henderson?
Lawrence Joseph Henderson was an American chemist who made significant contributions to the field of biochemistry. He is best known for his work on acid-base equilibrium and his derivation of the equation that later became known as the Henderson-Hasselbalch equation. Henderson’s research focused on the role of pH in biological systems, and his work laid the foundation for our understanding of how pH affects various physiological processes. His contributions continue to be highly regarded in the field of biochemistry.

History of Henderson-Hasselbalch Equation
The Henderson-Hasselbalch equation has a rich history dating back to the early 20th century. It was first derived by Lawrence Joseph Henderson, an American chemist, in 1908. Henderson’s equation provided a mathematical relationship between the pH of a solution and the acid dissociation constant (pKa) of a weak acid. This equation formed the basis for understanding the behavior of buffer solutions. Later, in 1917, Karl Albert Hasselbalch, a Danish chemist, re-expressed the equation in logarithmic terms, making it more accessible and widely applicable. The resulting equation, known as the Henderson-Hasselbalch equation, is still widely used today in various fields of chemistry and biochemistry.
Derivation of the Henderson Hasselbalch Equation
The Henderson-Hasselbalch equation can be derived from the definition of the acid dissociation constant (Ka). Consider a weak acid, HA, in water:
HA + H2O ⇌ A– + H3O+
The acid dissociation constant, Ka, can be defined as:
Ka = [A–][H3O+]/[HA]
Taking the negative logarithm of both sides, we get:
-log Ka = -log [A–][H3O+]/[HA]
Using the properties of logarithms, we can rewrite this equation as:
-log Ka = -log [A–] – log [H3O+] + log [HA]
We know that -log [H3O+] is equal to pH, and -log Ka is equal to pKa. Substituting these values, we get:
pKa = pH – log [A–]/[HA]
Rearranging the equation, we have:
pH = pKa + log [A–]/[HA]
This is the Henderson-Hasselbalch equation, which provides a relationship between the pH, pKa, and the concentrations of the conjugate base and weak acid.
Derivation of Henderson Hasselbalch Equation for Base
In a similar manner, we can derive the Henderson-Hasselbalch equation for a weak base. Consider the ionization of a weak base, B, in water:
B + H2O ⇌ OH– + BH+
The base dissociation constant, Kb, can be defined as:
Kb = [OH–][BH+]/[B]
Taking the negative logarithm of both sides, we get:
-log Kb = -log [OH–][BH+]/[B]
Using the properties of logarithms, we can rewrite this equation as:
-log Kb = -log [OH–] – log [BH+] + log [B]
We know that -log [OH–] is equal to pOH, and -log Kb is equal to pKb. Substituting these values, we get:
pKb = pOH – log [BH+]/[B]
Rearranging the equation, we have:
pOH = pKb + log [BH+]/[B]
This is the Henderson-Hasselbalch equation for a weak base, which provides a relationship between the pOH, pKb, and the concentrations of the conjugate acid and weak base.
Formula for Henderson-Hasselbalch Equation
The Henderson-Hasselbalch equation can be written as:
pH = pKa + log [A–]/[HA]
In this equation, pH represents the negative logarithm of the hydrogen ion concentration, pKa represents the negative logarithm of the acid dissociation constant, [A–] represents the molar concentration of the conjugate base, and [HA] represents the molar concentration of the weak acid. The Henderson-Hasselbalch equation is a useful tool for estimating the pH of a buffer solution when the concentrations of the acid and its conjugate base are known.
Limitations of the Henderson Hasselbalch Equation
While the Henderson-Hasselbalch equation is a valuable tool in estimating the pH of buffer solutions, it does have its limitations. Some of the limitations include:
- The equation assumes that the concentrations of the acid and its conjugate base at chemical equilibrium remain the same as the formal concentrations. In reality, the binding of protons to the base and the self-dissociation of water can affect the concentrations and lead to deviations from the predicted pH values.
- The Henderson-Hasselbalch equation is not applicable to strong acids and bases, as their ionization constants are much larger and the assumption of weak acid or base behavior does not hold.
- The equation does not take into account the effect of temperature on the acid dissociation constant, which can lead to deviations from the predicted pH values.
- The equation assumes that the buffer system is in equilibrium, which may not always be the case in real-life situations.
Despite these limitations, the Henderson-Hasselbalch equation remains a valuable tool in the field of chemistry and biochemistry for estimating the pH of buffer solutions.
Applications of Henderson Hasselbalch Equation
The Henderson-Hasselbalch equation has a wide range of applications in various fields of chemistry and biochemistry. Some of the key applications include:
- Buffer Solution Preparation: The Henderson-Hasselbalch equation is used to calculate the concentrations of acid and salt required to prepare buffer solutions of specific pH values. By adjusting the concentrations of the acid and its conjugate base, buffer solutions can be created with the desired pH.
- pH Estimation: The Henderson-Hasselbalch equation is used to estimate the pH of buffer solutions in chemical and biological systems. It provides a convenient and accurate method for determining the pH based on the concentrations of the acid and its conjugate base.
- Isoelectric Point Determination: The Henderson-Hasselbalch equation is used to calculate the isoelectric point of proteins. The isoelectric point is the pH at which the net charge of a protein is zero, and it can be determined by considering the acid-base properties of the amino acid residues in the protein.
- Acid-Base Reactions: The Henderson-Hasselbalch equation is used to calculate the equilibrium pH in acid-base reactions. It provides a quantitative understanding of how the pH changes as acids and bases react with each other.
Significance of Henderson Hasselbalch Equation
The Henderson-Hasselbalch equation is of great significance in the study of acid-base equilibrium and buffer systems. Its applications extend to various fields of chemistry and biochemistry. Some of the key points highlighting the significance of the Henderson-Hasselbalch equation are:
- pH Calculation: The Henderson-Hasselbalch equation provides a simple and effective way to calculate the pH of buffer solutions. By knowing the concentrations of the acid and its conjugate base, we can determine the pH with precision.
- Buffer Solution Design: The Henderson-Hasselbalch equation is used in designing buffer solutions with specific pH values. By manipulating the concentrations of the acid and its conjugate base, we can create buffer solutions that can resist changes in pH.
- Acid-Base Equilibrium: The Henderson-Hasselbalch equation is based on the principles of acid-base equilibrium. It allows us to understand and quantify the relationship between the pH, concentration of acid and its conjugate base, and the acid dissociation constant.
- Biological Systems: The Henderson-Hasselbalch equation is particularly relevant in the study of biological systems, where maintaining a specific pH is crucial for the proper functioning of enzymes, proteins, and other biomolecules.
How to Use Henderson Hasselbalch Equation?
To use the Henderson-Hasselbalch equation, follow these steps:
- Identify the weak acid and its conjugate base in the buffer solution.
- Determine the molar concentrations of the acid ([HA]) and its conjugate base ([A–]).
- Obtain the pKa value for the weak acid.
- Plug the values into the Henderson-Hasselbalch equation: pH = pKa + log [A–]/[HA].
- Calculate the logarithm of the ratio [A–]/[HA].
- Add the logarithm to the pKa value to obtain the pH of the buffer solution.
By following these steps, you can effectively use the Henderson-Hasselbalch equation to estimate the pH of buffer solutions.
Solved Examples on Henderson-Hasselbalch Equation
Example 1: Calculate the pH of a buffer solution made from 0.20M acetic acid (HC2H3O2) and 0.50M acetate ion (C2H3O2–). The acid dissociation constant (pKa) of acetic acid is 4.74.
Solution: Using the Henderson-Hasselbalch equation: pH = pKa + log [A–]/[HA]
Given: pKa = 4.74 [A–] = 0.50M [HA] = 0.20M
pH = 4.74 + log (0.50M / 0.20M) pH = 4.74 + log 2.5 pH = 4.74 + 0.40 pH = 5.14
Therefore, the pH of the buffer solution is 5.14.
Example 2: A buffer solution is prepared by mixing 0.10M ammonia (NH3) and 0.20M ammonium chloride (NH4Cl). The pKa of ammonia is 9.25. Calculate the pH of the buffer solution.
Solution: Using the Henderson-Hasselbalch equation: pH = pKa + log [A–]/[HA]
Given: pKa = 9.25 [A–] = 0.10M [HA] = 0.20M
pH = 9.25 + log (0.10M / 0.20M) pH = 9.25 + log 0.5 pH = 9.25 – 0.30 pH = 8.95
Therefore, the pH of the buffer solution is 8.95.
Example 3: A buffer solution is created by mixing 0.30M benzoic acid (C6H5COOH) and 0.50M sodium benzoate (C6H5COONa). The pKa of benzoic acid is 4.20. Calculate the pH of the buffer solution.
Solution: Using the Henderson-Hasselbalch equation: pH = pKa + log [A–]/[HA]
Given: pKa = 4.20 [A–] = 0.50M [HA] = 0.30M
pH = 4.20 + log (0.50M / 0.30M) pH = 4.20 + log 1.67 pH = 4.20 + 0.22 pH = 4.42
Therefore, the pH of the buffer solution is 4.42.
How Kunduz Can Help You Learn Henderson-Hasselbalch Equation?
At Kunduz, we understand the importance of mastering the Henderson-Hasselbalch equation in chemistry and biochemistry. We offer comprehensive study materials, step-by-step tutorials, and practice questions to help you understand and apply this equation effectively. Our expert educators are available to provide personalized guidance and support, ensuring that you have a solid grasp of the Henderson-Hasselbalch equation and its applications. With Kunduz, you can confidently approach your chemistry studies and achieve academic success.
