Polygons have long captivated mathematicians and enthusiasts alike with their diverse shapes and characteristics. From the simplicity of triangles to the complexity of polygons with numerous sides, each shape holds its own unique properties. Among these intriguing polygons is the heptagon, a seven-sided figure that exhibits fascinating properties and patterns. In this article, we will explore the world of heptagons, gaining an understanding of their definition, properties, types, formulas, and even solving example problems. So, let’s embark on this geometric journey and unravel the mysteries of the heptagon!
What is a Heptagon?
At its core, a heptagon is a polygon with seven sides and seven angles. The term “heptagon” is derived from the Greek words “hepta,” meaning seven, and “gon,” meaning sides. It is also known as a 7-gon or septagon. Heptagons can come in different forms, including regular and irregular heptagons, each with its own set of properties and characteristics.
Heptagon Formulas
Area of Heptagon
To calculate the area of a heptagon, we use the formula:
Area of a Heptagon = (7/4) * a² * cot(π/7)
Where “a” represents the length of each side of the heptagon.
Perimeter of Heptagon
The perimeter of a heptagon can be calculated by multiplying the length of one side by 7, since all sides of a regular heptagon are of equal length. The formula for the perimeter is:
Perimeter of a Heptagon = 7 * a
Where “a” represents the length of each side of the heptagon.
Let’s explore the area and perimeter of a regular heptagon through a solved example.
Solved Examples on Heptagon
Example 1: Find the area and perimeter of a regular heptagon with a side length of 5 cm.
Solution: Given: Side length (a) = 5 cm
To find the area of the heptagon, we can use the formula:
Area of a Heptagon = (7/4) * a² * cot(π/7)
Substituting the given value of “a” into the formula:
Area of a Heptagon = (7/4) * (5 cm)² * cot(π/7)
Calculating the area:
Area of a Heptagon = (7/4) * 25 cm² * cot(π/7)
Approximately, the area of the heptagon is 90.85 cm².
To find the perimeter of the heptagon, we can use the formula:
Perimeter of a Heptagon = 7 * a
Substituting the given value of “a” into the formula:
Perimeter of a Heptagon = 7 * 5 cm
Calculating the perimeter:
Perimeter of a Heptagon = 35 cm
Therefore, the area of the heptagon is 90.85 cm² and the perimeter is 35 cm.
Polygon Shapes
Before we delve deeper into the properties of heptagons, let’s take a moment to explore other important polygon shapes. Understanding the characteristics of these polygons will provide a foundation for comprehending the intricacies of heptagons. Here are some key polygon shapes:
Triangle
A triangle is a polygon with three sides and three angles. It is the simplest polygon shape, forming the building block for more complex polygons. Triangles can be classified based on the lengths of their sides and the measures of their angles. There are several types of triangles, including equilateral, isosceles, and scalene triangles.

Quadrilateral
A quadrilateral is a polygon with four sides and four angles. Like triangles, quadrilaterals can also be classified based on the lengths of their sides and the measures of their angles. Examples of quadrilaterals include squares, rectangles, parallelograms, and trapezoids.
Pentagon
A pentagon is a polygon with five sides and five angles. It is a versatile shape that can be found in various contexts, from architecture to nature. Pentagons can be classified based on the lengths of their sides and the measures of their angles. Regular pentagons have all sides and angles equal, while irregular pentagons have sides and angles of different measures.
Hexagon
A hexagon is a polygon with six sides and six angles. It is a widely recognized shape, often used in design and architecture. Like other polygons, hexagons can be classified based on the lengths of their sides and the measures of their angles. Regular hexagons have all sides and angles equal, while irregular hexagons have sides and angles of different measures.
Square
A square is a special type of quadrilateral with four equal sides and four right angles. It is known for its symmetry and stability, making it a popular shape in construction and design. All angles in a square measure 90 degrees, and all sides have equal length.
Rectangle
A rectangle is also a quadrilateral, but with four right angles. Unlike a square, a rectangle does not have all sides of equal length. However, opposite sides of a rectangle are parallel and equal in length, making it a versatile shape in various applications.

Parallelogram
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length. Like rectangles and squares, a parallelogram has four right angles. However, the angles in a parallelogram do not have to be 90 degrees.
Trapezoid
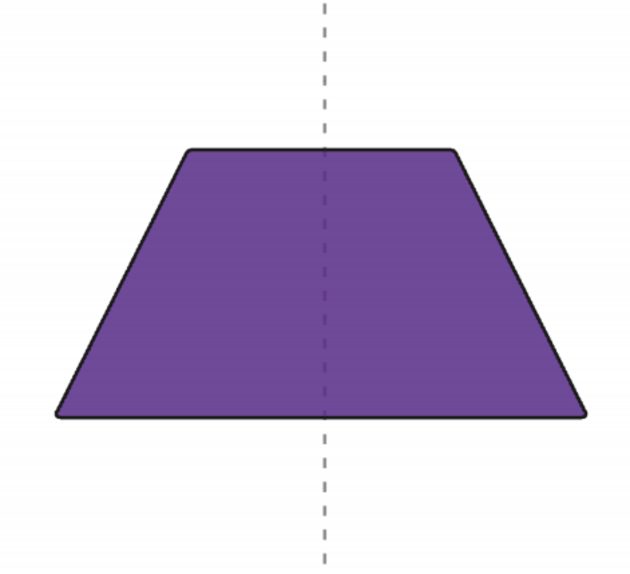
A trapezoid is a quadrilateral with only one pair of parallel sides. The non-parallel sides of a trapezoid are known as legs, while the parallel sides are called bases. Trapezoids can have different angles and side lengths, making them a diverse group of shapes.
Rhombus
A rhombus is a quadrilateral with four sides of equal length. Like rectangles and squares, a rhombus has opposite sides that are parallel to each other. However, unlike rectangles and squares, the angles in a rhombus do not have to be 90 degrees.
These polygon shapes lay the groundwork for understanding the properties and characteristics of heptagons. Let’s now shift our focus back to the unique features of heptagons and explore their angles in more detail.

Heptagon Angles
In a heptagon, the angles play a crucial role in determining its properties and symmetry. Let’s explore the angles of a heptagon in more detail:
Interior Angles of a Regular Heptagon
The interior angles of a regular heptagon are congruent, meaning they all have the same measure. To find the measure of each interior angle, we can use the formula:
Measure of each interior angle = (n - 2) × 180° / n
In the case of a regular heptagon, n = 7 (since it has 7 sides). Substituting this value into the formula, we get:
Measure of each interior angle = (7 - 2) × 180° / 7
Simplifying the equation, we find that the measure of each interior angle in a regular heptagon is approximately 128.57°.
Exterior Angles of a Regular Heptagon
The exterior angles of a regular heptagon are also congruent, meaning they all have the same measure. To find the measure of each exterior angle, we can use the formula:
Measure of each exterior angle = 360° / n
Using the value of n = 7 (number of sides in a heptagon), we can substitute it into the formula:
Measure of each exterior angle = 360° / 7
Simplifying the equation, we find that the measure of each exterior angle in a regular heptagon is approximately 51.43°.
These interior and exterior angles contribute to the overall shape and symmetry of a heptagon. The distribution of these angles determines whether a heptagon is regular or irregular. Let’s explore the types of heptagons based on their symmetry and characteristics.
Types of Heptagon
Heptagons can be classified into different types based on their symmetry, side lengths, and angle measures. Let’s explore the various types of heptagons:
Regular Heptagon
A regular heptagon is a heptagon with all sides and angles equal. In other words, each side has the same length, and each interior angle measures the same. The regular heptagon is a symmetrical shape that exhibits uniformity and balance.
Irregular Heptagon
An irregular heptagon does not have all sides and angles equal. Its sides and angles can have varying lengths and measures. Unlike regular heptagons, irregular heptagons lack symmetry and may appear more complex in their overall shape.
Convex Heptagon
A convex heptagon is a heptagon in which all interior angles measure less than 180 degrees. The sides of a convex heptagon do not intersect when extended. Convex heptagons can be either regular or irregular, depending on the lengths of their sides and measures of their angles.
Concave Heptagon
A concave heptagon has at least one interior angle greater than 180 degrees. It may also have sides that intersect when extended. Concave heptagons can be either regular or irregular, depending on the lengths of their sides and measures of their angles. The presence of interior angles greater than 180 degrees gives concave heptagons a unique and distinct shape.
These types of heptagons highlight the diverse possibilities within this seven-sided polygon. Now, let’s explore the properties that set heptagons apart from other polygon shapes.
Properties of Heptagon
Heptagons possess several distinctive properties that make them unique among polygons. Understanding these properties is crucial to comprehend the characteristics and behavior of heptagons. Here are some key properties of heptagons:
- Number of Sides: A heptagon has seven sides, making it a septagonal figure.
- Number of Angles: A heptagon has seven angles, each formed at the intersection of two sides.
- Sum of Interior Angles: The sum of the interior angles in any heptagon is always 900 degrees. This property holds true for both regular and irregular heptagons.
- Sum of Exterior Angles: The sum of the exterior angles in any heptagon is always 360 degrees. Again, this property applies to both regular and irregular heptagons.
- Diagonals: A heptagon has 14 diagonals, which are line segments connecting non-adjacent vertices. These diagonals play a crucial role in the overall structure and properties of a heptagon.
- Regular Heptagons: Regular heptagons are a subset of heptagons in which all sides and angles are equal. The presence of symmetry and uniformity in regular heptagons makes them particularly intriguing.
- Triangles in Heptagon: It is fascinating to note that a heptagon can be divided into five triangles, illustrating the interconnectedness of polygons and their composite shapes.
These properties contribute to the overall understanding and analysis of heptagons. By examining these properties, we gain valuable insights into the symmetry, angles, and structure of these unique polygons. Now, let’s explore some frequently asked questions about heptagons to address common queries and misconceptions.
Frequently Asked Questions on Heptagon
Can a heptagon have all equal angles?
No, a heptagon cannot have all equal angles unless it is a regular heptagon. In an irregular heptagon, the angles can have different measures.
What is the sum of the interior angles of a heptagon?
The sum of the interior angles of any heptagon is always equal to (7 – 2) * 180 degrees, which is 900 degrees.
Can a heptagon have parallel sides?
No, a heptagon cannot have parallel sides because each side connects to the adjacent sides, and they cannot be parallel while still forming a closed figure.
What is the formula to find the measure of each interior angle in a regular heptagon?
The measure of each interior angle in a regular heptagon can be calculated using the formula: (n – 2) * 180 degrees / n. In the case of a heptagon, where n = 7 (since it has 7 sides), the formula simplifies to (7 – 2) * 180 degrees / 7.
What is the formula to find the measure of each exterior angle in a heptagon?
The measure of each exterior angle in any heptagon, regular or irregular, can be found by subtracting the measure of the corresponding interior angle from 180 degrees.
Can a heptagon be divided into congruent triangles?
No, a heptagon cannot be divided into congruent triangles, as the angles and sides of the heptagon do not allow for such a division.
What is the relationship between heptagons and circles?
Heptagons can be inscribed within circles, meaning all the vertices of the heptagon lie on the circumference of a circle. The center of the circle is the point of intersection of the perpendicular bisectors of the sides of the heptagon.
Are there any famous mathematical problems involving heptagons?
Yes, one of the most famous problems involving heptagons is the construction of a regular heptagon using only a compass and straightedge. This problem, known as the “trisecting the angle” problem, has challenged mathematicians for centuries.
How many sides does a heptagon have?
A heptagon has seven sides, making it a septagonal figure.
These frequently asked questions shed light on common queries and misconceptions surrounding heptagons. By addressing these questions, we can deepen our understanding of these unique polygons and their properties. Now, let’s apply our knowledge to solve some example problems involving heptagons.
Solved Examples on Heptagon
Let’s consider a couple of examples to illustrate the concepts discussed above.
Example 1:
Find the area and perimeter of a regular heptagon whose side length is 6 cm.
Solution:
Given that the side length of the heptagon, denoted as ‘a’, is 6 cm.
We know that the perimeter (P) of a regular heptagon is calculated using the formula P = 7a. Substituting a = 6 cm into the formula, we get:
P = 7 x 6 cm = 42 cm
Therefore, the perimeter of the heptagon is 42 cm.
Next, we’ll calculate the area (A) of the heptagon using the formula A = 3.634a². Substituting a = 6 cm into the formula, we get:
A = 3.634 x (6 cm)² = 3.634 x 36 sq.cm = 131.624 sq.cm
Therefore, the area of the heptagon is approximately 131.624 square cm.
Example 2:
Find the measure of each interior angle in a regular heptagon.
Solution:
We use the formula for the measure of each interior angle in a regular polygon: (n-2) x 180 degrees / n, where n represents the number of sides. For a heptagon, n equals 7.
Substituting n = 7 into the formula, we get:
Interior angle = (7 – 2) x 180 degrees / 7 = 5 x 180 degrees / 7 = 900 degrees / 7 = approximately 128.57 degrees
Therefore, each interior angle of a regular heptagon measures approximately 128.57 degrees.
How Kunduz Can Help You Learn Heptagon?
By understanding the concept of heptagons, you’re not only expanding your mathematical knowledge but also enhancing your spatial reasoning and problem-solving skills. So go ahead and explore the fascinating world of heptagons, and don’t hesitate to seek help if you need it. Remember, every step you take in learning brings you closer to your academic goals!
For readers exploring the properties of heptagon and interested in a broader understanding of polygons, we offer various other polygon pages. These resources delve into the formulas, characteristics, and classifications of polygons, providing a comprehensive exploration of geometric shapes beyond the heptagon:
What is Quadrilateral? Properties, Definition, Types, Area, Solved Examples, FAQs
Pentagon: Definition, Shape, Properties, Types, Formula & Example
Octagon Shape: Definition, Properties, Formula, Examples, Sides & Angles
