In the realm of mathematics, understanding the behavior of functions is crucial for analyzing their graphs. One important concept that helps us comprehend the end behavior of a function is the horizontal asymptote. While vertical asymptotes describe the behavior of a function as the input approaches positive or negative infinity, horizontal asymptotes describe the behavior of a function as the input gets significantly large or small.
What is Asymptote?
Before delving into the specifics of horizontal asymptotes, it’s important to understand the general concept of asymptotes. An asymptote is a line that a curve approaches but never touches or crosses. It provides insight into the behavior of a function as the input values approach certain limits.
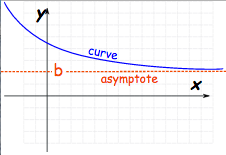
What is a Horizontal Asymptote?
The horizontal asymptote (HA) of a function is a horizontal line represented by the equation y = b. The curve of the function approaches this line as the value of x (the input) heads towards positive or negative infinity. However, it’s important to note that the curve may never actually touch or cross this line.
How to Find Horizontal Asymptotes?
Identifying horizontal asymptotes involves analyzing the function and its behavior as x approaches infinity. The process varies depending on the type of function you’re dealing with.
Horizontal Asymptotes From Graph
One way to determine the horizontal asymptote is by examining the graph of the function. By observing the behavior of the graph as x gets significantly large or small, we can infer the presence and position of a horizontal asymptote.
For example, consider the rational function f(x) = (2x – 1) / (3x + 2). By analyzing the graph of this function, we can observe that as x approaches positive or negative infinity, the graph approaches the horizontal line y = 2/3. This indicates that the function has a horizontal asymptote at y = 2/3.
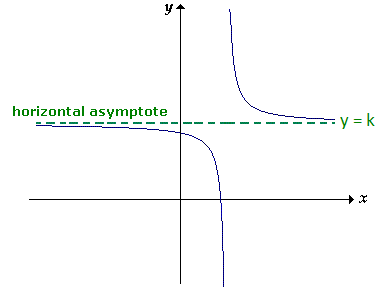
Horizontal Asymptotes From Equation
Another method to find the horizontal asymptote is by analyzing the equation of the function. By comparing the degrees of the numerator and denominator, we can determine the presence and position of the horizontal asymptote.
Finding Horizontal Asymptotes of Rational Functions
A rational function is a function that can be expressed as the ratio of two polynomial functions. To find the horizontal asymptote of a rational function, we can follow a set of rules based on the degrees of the numerator and denominator:
- If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is at y = 0 (the x-axis).
- If the degree of the numerator is equal to the degree of the denominator, the horizontal asymptote is at y = the ratio of the leading coefficients of the numerator and denominator.
- If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote. However, there may be a slant or oblique asymptote if the degree of the numerator is exactly one greater than the degree of the denominator.
Let’s consider the rational function f(x) = (x^3 – 1) / (3 + x^2) as an example. The degree of the numerator is 3, and the degree of the denominator is 2. Since the degree of the numerator is greater than the degree of the denominator, this function does not have a horizontal asymptote.
Finding Horizontal Asymptote of an Exponential Function
Exponential functions have a different approach to determining horizontal asymptotes. In an exponential function of the form f(x) = a * b^(kx) + c, the horizontal asymptote is always at y = c. If c is equal to 0, then the horizontal asymptote is at y = 0 (the x-axis).
For instance, let’s consider the exponential function f(x) = 4^x + 1. Since the constant term is 1, the horizontal asymptote is at y = 1.
Horizontal Asymptotes Using Limits
In some cases, we can determine the horizontal asymptote of a function by evaluating the limits as x approaches positive or negative infinity. By analyzing the behavior of the function as x gets infinitely large or small, we can infer the presence and position of the horizontal asymptote.
For example, consider the function f(x) = (x^2 + 3) / (2x). By taking the limits as x approaches positive or negative infinity, we can find that the function approaches y = 1/2. Hence, the horizontal asymptote is at y = 1/2.
Horizontal Asymptotes Formula
As mentioned earlier, when the degrees of the numerator and denominator of a rational function are the same, the horizontal asymptote can be calculated using a simple formula. If the rational function is in the form f(x) = (P(x)) / (Q(x)), where P(x) and Q(x) are polynomials, the horizontal asymptote is given by:
y = (leading coefficient of P(x)) / (leading coefficient of Q(x))
For example, consider the rational function f(x) = (2x^2 – 1) / (x^2 + 3). In this case, the degrees of the numerator and denominator are the same, and the leading coefficients are 2 and 1, respectively. Therefore, the horizontal asymptote is at y = 2/1 = 2.
Can a Horizontal Asymptote Cross the Curve?
One common misconception is that a horizontal asymptote cannot cross the curve of a function. However, this is not true. Unlike vertical asymptotes, which the graph of a function can never touch, a horizontal asymptote can be crossed by the function’s graph.
For example, consider the function f(x) = x / (x^2 + 1). The horizontal asymptote of this function is at y = 0 (the x-axis). However, if we solve the equation x / (x^2 + 1) = 0, we find that x = 0. This means that the graph of the function crosses the horizontal asymptote at (0, 0). It’s important to note that crossing the asymptote does not invalidate its presence or significance.
Horizontal Asymptote Rules
To summarize the rules for horizontal asymptotes:
- If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is at y = 0 (the x-axis).
- If the degree of the numerator is equal to the degree of the denominator, the horizontal asymptote is at y = the ratio of the leading coefficients of the numerator and denominator.
- If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote. However, there may be a slant or oblique asymptote if the degree of the numerator is exactly one greater than the degree of the denominator.
These rules provide a systematic approach to finding the horizontal asymptotes of rational functions.
How to Graph Horizontal Asymptote?
Graphing a horizontal asymptote is relatively straightforward. Once you have determined the equation of the horizontal asymptote, you can plot it on the graph to visualize its position relative to the function.
For example, if the horizontal asymptote is at y = 2, you can draw a dashed horizontal line at the height of y = 2 on the graph. This line represents the behavior of the function as x approaches positive or negative infinity.
It’s important to note that the graph of the function may touch or intersect the horizontal asymptote at certain points. This is completely acceptable and does not invalidate the presence or significance of the asymptote.

Horizontal Asymptote Equation
The equation of a horizontal asymptote can be determined using the rules discussed earlier. If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is at y = 0 (the x-axis). If the degrees are equal, the horizontal asymptote is given by the ratio of the leading coefficients of the numerator and denominator. If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.
For example, let’s consider the rational function f(x) = (3x^2 + 2) / (x^2 + 1). The degrees of the numerator and denominator are the same, and the leading coefficients are 3 and 1, respectively. Therefore, the equation of the horizontal asymptote is y = 3/1 = 3.
How to Identify Horizontal Asymptotes
To identify horizontal asymptotes, you need to analyze the behavior of the function as x approaches positive or negative infinity. By evaluating the limits of the function at these extremes, you can determine the presence and position of the horizontal asymptote.
If the limits as x approaches positive or negative infinity yield a real number, then the function has a horizontal asymptote at that value. If the limits give infinity or negative infinity, there is no horizontal asymptote. It’s important to note that horizontal asymptotes provide information about the long-term behavior of the function and do not necessarily imply any restrictions on the function’s values or behavior within a finite range.
Horizontal Asymptotes vs. Vertical Asymptotes
Horizontal asymptotes and vertical asymptotes serve different purposes and provide different information about the behavior of a function.
Vertical asymptotes describe the behavior of a function as the input approaches positive or negative infinity. They are vertical lines that the graph of the function cannot touch or cross. Vertical asymptotes are determined by the zeroes of the denominator in a rational function.
On the other hand, horizontal asymptotes describe the behavior of a function as the input gets significantly large or small. They are horizontal lines that the graph of the function approaches but does not intersect. Horizontal asymptotes are determined by comparing the degrees of the numerator and denominator in a rational function.
While vertical asymptotes indicate specific behavior near the origin, horizontal asymptotes provide general behavior far off to the sides of the graph. Vertical and horizontal asymptotes complement each other in providing a comprehensive understanding of a function’s behavior.
Differences Between Horizontal Asymptotes and Vertical Asymptotes
To compare and contrast horizontal and vertical asymptotes, let’s examine their key characteristics:
| Aspect | Horizontal Asymptotes | Vertical Asymptotes |
|---|---|---|
| Definition | Horizontal lines that the graph approaches as x approaches positive or negative infinity | Vertical lines that the graph approaches as x approaches certain values |
| Behavior | Describes the end behavior of the function as x gets large or small | Indicates specific behavior near the origin |
| Touching/Crossing | Can be touched or crossed by the graph of the function | Cannot be touched or crossed by the graph of the function |
| Determination | Analyzing the limits of the function as x approaches infinity | Finding the zeroes of the denominator in a rational function |
| Position | Far off to the sides of the graph | Close to the origin on the graph |
| Representation | y = b (where b is a real number) | x = a (where a is a real number) |
Understanding these differences helps us grasp the distinct roles and implications of horizontal and vertical asymptotes in analyzing the behavior of functions.
Asymptotes of a Hyperbola
Hyperbolas, which are conic sections, also have asymptotes. Unlike vertical and horizontal asymptotes, which are straight lines, the asymptotes of a hyperbola are oblique lines. These asymptotes help define the overall shape and behavior of the hyperbola.
For example, the equation of a hyperbola in standard form is given by (x^2 / a^2) – (y^2 / b^2) = 1. The oblique asymptotes of this hyperbola can be determined by analyzing the coefficients in the equation.
The equations of the oblique asymptotes for the given hyperbola are y = (b / a) * x and y = -(b / a) * x. These lines provide a sense of direction and symmetry for the hyperbola.
Solved Examples on Horizontal Asymptote
Let’s solve a few examples to solidify our understanding of horizontal asymptotes:
Example 1: Find the horizontal asymptote of the function f(x) = (2x^2 + 1) / (3x^2 – x + 1).
To find the horizontal asymptote, we compare the degrees of the numerator and denominator. Since both have the same degree (2), the horizontal asymptote is given by the ratio of the leading coefficients. In this case, it is y = 2/3.
Example 2: Determine the horizontal asymptote of the function f(x) = (5x^3 – 2x^2 + 1) / (2x^3 + 3x – 1).
By comparing the degrees of the numerator and denominator, we find that the degree of the numerator is greater. Therefore, there is no horizontal asymptote for this function.
Example 3: Consider the function f(x) = e^x + 1. What is the horizontal asymptote, if any?
Since the function is an exponential function, the horizontal asymptote is always at y = c, where c is the constant term. In this case, the horizontal asymptote is y = 1.
These examples highlight the application of the rules discussed earlier in finding the horizontal asymptotes of various functions.
How Kunduz Can Help You Learn Horizontal Asymptote?
At Kunduz, we understand the importance of mastering mathematical concepts like horizontal asymptotes. Our platform offers comprehensive learning materials, including video tutorials, practice problems, and step-by-step explanations, to help you understand and apply these concepts effectively.
Whether you’re a student looking to strengthen your math skills or an educator seeking resources to support your teaching, Kunduz provides a user-friendly and accessible platform for learning about horizontal asymptotes and other mathematical topics.
With our engaging and interactive content, you can explore the intricacies of horizontal asymptotes and gain a deeper understanding of their significance in analyzing the behavior of functions. Our materials are designed to cater to different learning styles and provide a solid foundation for further mathematical exploration.
Discover the power of Kunduz and unlock your mathematical potential today!
