When we think of lines, one of the fundamental types that comes to mind is the horizontal line. It is a line that extends from left to right, parallel to the horizon. In geometry, horizontal lines are significant as they have distinct properties and applications. Understanding the concept of a horizontal line is essential for various fields, including mathematics, engineering, and design.
What is the Horizontal Line?
A horizontal line is a straight line that runs parallel to the horizon or the ground. It can be visualized as a line that extends from left to right or right to left. The term “horizontal” is derived from the word “horizon,” which refers to the line where the earth’s surface appears to meet the sky. Horizontal lines are often associated with stability, balance, and tranquility.
In coordinate geometry, horizontal lines are lines that are parallel to the x-axis. They have a constant y-coordinate, while the x-coordinate can vary. This means that all points on a horizontal line share the same y-coordinate.

Horizontal Line Equation
The equation of a horizontal line is of the form y = c, where c is a constant value representing the y-intercept of the line. Since all points on a horizontal line have the same y-coordinate, the equation indicates that the line passes through all points where the y-coordinate is equal to c.
For example, if we have a horizontal line passing through the point (2, 5), the equation of the line would be y = 5. This means that all points on the line will have a y-coordinate of 5, regardless of their x-coordinate.
Slope of Horizontal Line
The slope of a line represents its inclination or steepness. However, when it comes to horizontal lines, the slope is always zero. This is because horizontal lines have no vertical movement and remain at a constant height from the ground. In other words, there is no change in the y-coordinate as we move along a horizontal line.
To calculate the slope of a line, we use the formula:
Slope = (Change in y-coordinate) / (Change in x-coordinate)
Since the change in the y-coordinate is always zero for a horizontal line, the numerator of the formula becomes zero. Dividing zero by any non-zero value still yields zero, resulting in a slope of zero.
How to Draw a Horizontal Line?
Drawing a horizontal line is relatively simple. All you need is a ruler or a straight edge to guide your drawing.
Here are the steps to draw a horizontal line:
- Start by placing the ruler or straight edge on a piece of paper or a drawing surface.
- Ensure that the ruler is parallel to the edge of the page or the desired direction for the horizontal line.
- Hold the ruler firmly and draw a straight line from left to right or right to left using a pencil or pen.
- The line should remain parallel to the ruler and have a consistent distance from the edge of the page.
By following these steps, you can draw a precise and accurate horizontal line.
Graphing a Horizontal Line
Graphing a horizontal line on a coordinate plane involves plotting points with a constant y-coordinate. Since all points on a horizontal line share the same y-coordinate, the line will appear as a straight, level line parallel to the x-axis.
To graph a horizontal line, follow these steps:
- Identify the y-coordinate of the point through which the horizontal line passes.
- Plot multiple points with the same y-coordinate but different x-coordinates.
- Connect the plotted points with a straight line, ensuring that it remains parallel to the x-axis.
- Extend the line in both directions to show that it continues infinitely.
For example, if we want to graph the equation y = 3, which represents a horizontal line passing through the point (0, 3), we would plot points such as (1, 3), (2, 3), (-1, 3), and so on. Connecting these points would result in a horizontal line at y = 3.
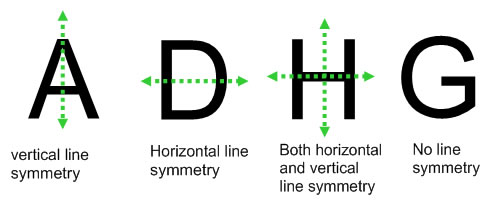
Horizontal Line Symmetry
Symmetry is a fundamental concept in geometry, and horizontal lines play a role in this concept. A horizontal line can have reflective symmetry, also known as line symmetry or mirror symmetry. When a shape or figure is reflected along a horizontal line, the resulting image is identical to the original shape.
For example, consider the letter “A.” If we draw a horizontal line through the center of the letter, the top and bottom halves will be mirror images of each other. This demonstrates horizontal line symmetry.
Horizontal line symmetry is also present in many other shapes and figures, such as squares, rectangles, and circles. When a shape has horizontal line symmetry, it means that it can be divided into two equal halves through a horizontal line, and each half will be a mirror image of the other.
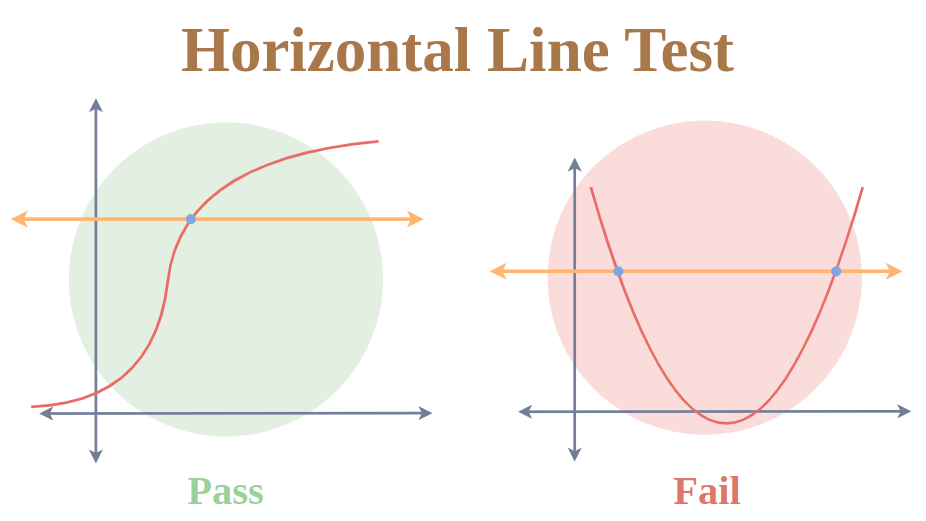
Horizontal Line Test
The horizontal line test is a method used to determine whether a function is one-to-one or injective. In other words, it helps identify if a function has a unique output for every input.
To perform the horizontal line test, imagine drawing a horizontal line across the graph of a function. If the line intersects the graph in more than one point, then the function fails the test and is not one-to-one. On the other hand, if the line intersects the graph at most once, the function passes the test and is considered one-to-one.
This test is based on the fact that a vertical line can intersect a graph at most once, while a horizontal line can intersect it multiple times if the function is not one-to-one.
Horizontal Line Segment
In geometry, a line segment is a portion of a line that is bounded by two distinct points. A horizontal line segment is a line segment that is parallel to the x-axis and has a constant y-coordinate. The x-coordinate of the points on the line segment can vary.
Horizontal line segments are commonly found in various shapes and figures. For example, in a rectangle, the top and bottom sides are horizontal line segments. Similarly, in a square, all four sides are horizontal line segments.
Horizontal vs. Vertical Lines
Horizontal and vertical lines are two fundamental types of lines that have distinct characteristics and applications. Understanding the difference between these two types is crucial in geometry and other fields.
A horizontal line is one that extends from left to right, parallel to the horizon or the ground. It has a slope of zero and has the equation y = c, where c is a constant representing the y-coordinate of all points on the line.
On the other hand, a vertical line is one that extends from top to bottom, perpendicular to the horizon or the ground. It has an undefined slope, and its equation is x = c, where c is a constant representing the x-coordinate of all points on the line.
Horizontal and vertical lines are perpendicular to each other. When a horizontal and vertical line intersect, they form a right angle, which measures 90 degrees. This perpendicular relationship is a key concept in geometry and is used in various applications, such as determining angles and constructing shapes.
| Horizontal Lines | Vertical Lines |
|---|---|
| They are sleeping lines. | They are standing lines. |
| They are parallel to the x-axis. | They are parallel to the y-axis. |
| They have a slope of zero. | They have an undefined slope. |
| The y-coordinates are constant for different x-coordinates. | The x-coordinates are constant for different y-coordinates. |
Frequently Asked Questions on Horizontal Line
Is “horizontal” from side to side?
Yes, a horizontal line extends from side to side, parallel to the horizon or the ground. It does not have any vertical movement.
Is horizontal up or down?
Horizontal lines are neither up nor down. They are parallel to the horizon or the ground and extend from left to right or right to left.
Are horizontal lines at 0 degrees?
Yes, horizontal lines have a slope of zero degrees. This means that they do not have any inclination or steepness.
What does a Horizontal Line Look Like?
A horizontal line appears as a straight, level line that extends from left to right or right to left. It does not have any vertical movement and remains at a constant height from the ground.
What are the Properties of Horizontal Lines?
Horizontal lines have several properties:
- They have a slope of zero.
- All points on a horizontal line share the same y-coordinate.
- Horizontal lines are parallel to the x-axis.
- They do not intersect the x-axis.
Is A Horizontal Line A Function?
A horizontal line is not a function because it fails the vertical line test. Since a horizontal line has a constant y-coordinate, it does not pass the test for unique x-values for each y-value.
Solved Examples on Horizontal Line
Example 1: Find the equation of the horizontal line passing through the point (3, 5).
Solution: Since the line is horizontal, all points on the line will have the same y-coordinate. Therefore, the equation of the line is y = 5.
Example 2: Determine whether the function f(x) = 2x – 3 is one-to-one.
Solution: To determine if the function is one-to-one, we can perform the horizontal line test. If a horizontal line intersects the graph of the function at more than one point, then the function is not one-to-one.
Let’s consider a horizontal line y = c, where c is a constant. To find the points of intersection, we substitute y = c into the equation of the function:
c = 2x – 3
Solving for x, we get:
2x = c + 3 x = (c + 3)/2
Since the equation is linear, we see that for every value of c, there is a unique value of x. Therefore, the function is one-to-one.
Example 3: Find the equation of the horizontal line passing through the point (1, -1).
Solution: For a horizontal line passing through a point (x, y), the equation is y = k, where k is the y-coordinate of the point. In this case, the equation of the line would be y = -1.
How Kunduz Can Help You Learn Horizontal Line?
Kunduz is an educational platform that provides comprehensive resources and assistance to help you learn about horizontal lines and other mathematical concepts. Whether you are a student, teacher, or simply interested in expanding your knowledge, Kunduz offers a range of materials tailored to your needs.
Through Kunduz, you can access step-by-step tutorials, interactive exercises, practice problems, and solved examples related to horizontal lines. These resources are designed to enhance your understanding and mastery of the topic. Additionally, Kunduz provides personalized support and guidance to address any questions or difficulties you may have.
