In mathematics, rationalizing the denominator is a crucial step to simplify calculations involving fractions. When we rationalize the denominator, we eliminate any radical expressions, such as square roots or cube roots, from the denominator. This process allows us to work with rational numbers, making calculations easier and more straightforward. In this article, we will explore different methods of rationalizing the denominator, understand the concept of rational numbers, and provide step-by-step examples to enhance your understanding.
An Introduction to Rationalize the Denominator
Rationalizing the denominator is a technique used in algebra to simplify fractions by removing any radical expressions from the denominator. The term “rationalize” means to make rational or to bring the fraction to its simplest form. By rationalizing the denominator, we ensure that the denominator becomes a rational number, which is a number that can be expressed as a fraction with an integer numerator and a non-zero integer denominator.
What is Rationalizing the Denominator?
Rationalizing the denominator involves multiplying both the numerator and the denominator of a fraction by a suitable value to eliminate the radical expression in the denominator. The value we multiply by, known as the rationalizing factor, is carefully chosen to ensure that the denominator becomes a rational number. By rationalizing the denominator, we simplify the fraction and make it easier to perform calculations.
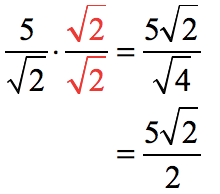
What is a Rational Number?
Before we delve into rationalizing the denominator, let’s understand what a rational number is. In mathematics, a rational number is any number that can be expressed as a fraction, where the numerator and denominator are both integers, and the denominator is not zero. Rational numbers can be positive, negative, or zero.
For example, the numbers 2, -3, and 0 are rational numbers because they can be written as fractions: 2/1, -3/1, and 0/1. Similarly, fractions such as 3/4, -5/2, and 1/5 are also rational numbers. Rational numbers can be represented on the number line and can be operated using arithmetic operations like addition, subtraction, multiplication, and division.
What is a Denominator?
In a fraction, the denominator represents the total number of equal parts into which the whole object is divided. It is the number at the bottom of the fraction that indicates the type of fraction described by the numerator. The denominator can be any positive integer, except for zero, as division by zero is undefined.
For example, in the fraction 3/5, the denominator is 5, indicating that the whole object is divided into 5 equal parts. Similarly, in the fraction 1/2, the denominator is 2, indicating that the whole object is divided into 2 equal parts.
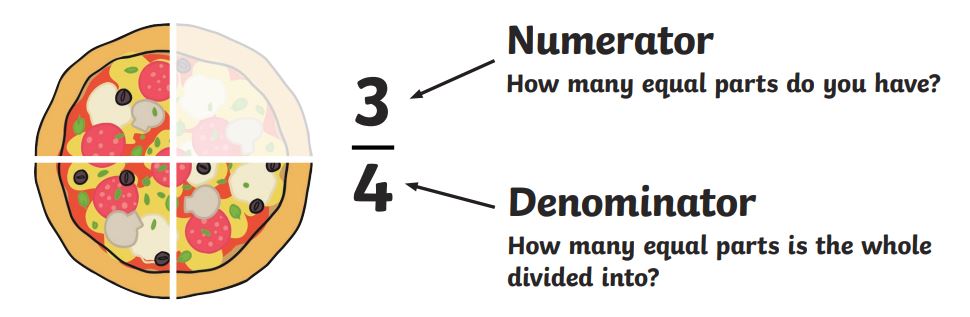
Numerator and Denominator
In a fraction, the numerator represents the number of parts of the whole object that we are considering. It is the number at the top of the fraction that indicates the count of the part of the object present in the given fraction. The numerator can be any integer, positive or negative, including zero.
For example, in the fraction 2/5, the numerator is 2, indicating that we have 2 parts of the whole object. In the fraction -3/4, the numerator is -3, indicating that we have -3 parts of the whole object. And in the fraction 0/1, the numerator is 0, indicating that we have no parts of the whole object.
The numerator and denominator together form a fraction, representing a ratio or a comparison between two quantities.
How to Rationalize the Denominator?
Rationalizing the denominator can be done using different methods depending on the type of denominator we are dealing with. Let’s explore the methods of rationalizing the denominator with single terms, two terms, three terms, and variables.
Rationalize the Denominator with Single Term
When the denominator of a fraction contains a single radical term, rationalizing the denominator is relatively simple. We can multiply both the numerator and the denominator by the same radical term to eliminate the radical from the denominator. By doing so, we obtain a rational denominator.
Let’s consider an example to understand the process:
Example 1: Rationalize the denominator of the fraction 1/√2
To rationalize the denominator, we multiply the numerator and the denominator by √2:
(1/√2) x (√2/√2) = √2/(√2)2 = √2/2
By multiplying both the numerator and the denominator by √2, we have successfully rationalized the denominator, which is now a rational number.
Let’s consider a few more examples to reinforce the concept:
Example 2: Rationalize the denominator of the fraction 1/√3
To rationalize the denominator, we multiply the numerator and the denominator by √3:
(1/√3) x (√3/√3) = √3/(√3)2 = √3/3
Example 3: Rationalize the denominator of the fraction 1/√5
To rationalize the denominator, we multiply the numerator and the denominator by √5:
(1/√5) x (√5/√5) = √5/(√5)2 = √5/5
By multiplying both the numerator and the denominator by the respective radical terms, we have obtained rational denominators in these examples.
Rationalize the Denominator with Two Terms
When the denominator of a fraction contains two terms along with a radical, we need to multiply both the numerator and the denominator by the conjugate of the denominator. The conjugate is obtained by changing the sign between the two terms in the denominator.
Let’s consider an example to understand the process:
Example: Rationalize the denominator for the fraction 2/(√3+5)
In this example, the denominator has one radical term and a whole number added to it. To rationalize the denominator, we multiply both the numerator and the denominator by the conjugate of the denominator, which is √3 – 5.
(2/(√3+5)) x ((√3-5)/(√3-5))
Using the formula (a+b)(a-b) = a^2 – b^2, we simplify the expression:
((2)(√3-5))/((√3)^2 – (5)^2) = (2)(√3-5)/(3 – 25) = (2)(√3-5)/(-22) = -2(√3-5)/22
By multiplying both the numerator and the denominator by the conjugate of the denominator, we have successfully rationalized the denominator. The fraction is now in its simplest form.
Rationalize the Denominator With Three Terms
Rationalizing the denominator with three terms involves grouping the terms as a sum of two terms and then applying the same method as rationalizing the denominator with two terms. By multiplying both the numerator and the denominator by the conjugate of the denominator, we eliminate the radicals from the denominator.
Let’s consider an example to understand the process:
Example: Rationalize the denominator for the fraction (5 – √3)/(2 + √5 + √3)
To rationalize the denominator, we group the terms as (2 + √5) + √3 and multiply both the numerator and the denominator by the conjugate of the denominator, which is (2 + √5) – √3.
((5 – √3)/((2 + √5) + √3)) x (((2 + √5) – √3)/((2 + √5) – √3))
Using the formula (a+b)(a-b) = a^2 – b^2, we simplify the expression:
((5 – √3)((2 + √5) – √3))/((2 + √5)^2 – (√3)^2) = ((5 – √3)(2 + √5) – (5 – √3)(√3))/((2 + √5)^2 – (√3)^2) = (10 + 5√5 – 2√3 – √15 – 5√3 + 3)/((2 + √5)^2 – 3) = (13 – √3 – √15 + 5√5 – 5√3)/((2 + √5)^2 – 3) = (13 – 6√3 – √15 + 5√5)/((2 + √5)^2 – 3)
By multiplying both the numerator and the denominator by the conjugate of the denominator, we have successfully rationalized the denominator. The fraction is now in its simplest form.
Rationalize the Denominator with Variables
Rationalizing the denominator with variables involves applying the same principles as rationalizing the denominator with radical terms. By multiplying both the numerator and the denominator by an appropriate value, we eliminate the radicals from the denominator and obtain a rational denominator.
Let’s consider an example to understand the process:
Example: Rationalize the denominator and find the value of x and y for the expression (5 + 4√3)/(4 + 5√3) = x + y√3
To rationalize the denominator and find the value of x and y, we multiply the numerator and the denominator by the conjugate of the denominator, which is (4 – 5√3).
((5 + 4√3)/(4 + 5√3)) x ((4 – 5√3)/(4 – 5√3))
Using the formula (a+b)(a-b) = a^2 – b^2, we simplify the expression:
((5 + 4√3)(4 – 5√3))/((4)^2 – (5√3)^2) = ((5)(4) + (5)(-5√3) + (4√3)(4) + (4√3)(-5√3))/((4)^2 – (5√3)^2) = (20 – 25√3 + 16√3 – 60)/((4)^2 – (5√3)^2) = (-40 – 9√3)/(-59)
Comparing the expression with x + y√3, we can determine the values of x and y:
x = -40/(-59) = 40/59 y = -9/(-59) = 9/59
By multiplying both the numerator and the denominator by the conjugate of the denominator, we have successfully rationalized the denominator and found the values of x and y.
How to Rationalize the Denominator Calculator?
If you need to rationalize the denominator of a fraction and want to simplify the process, you can use a rationalize the denominator calculator. This calculator deals with different types of radical division, including radical/radical, sum/radical, radical/sum, and sum/sum. The calculator performs the rationalization of the denominator and provides the simplified result.
Radical / Radical – (a * ⁿ√b) / (x * ᵏ√y)
To rationalize the denominator in this case, you need to multiply the expression by the rationalizing factor, which is ᵏ√(yᵏ⁻¹) / ᵏ√(yᵏ⁻¹). This will result in the denominator x * ᵏ√y * ᵏ√(yᵏ⁻¹) = x * ᵏ√(yᵏ) = x * y.
Sum / Radical – (a * ⁿ√b + c * ᵐ√d) / (x * ᵏ√y)
Similar to the previous case, you need to multiply the expression by the rationalizing factor, which is (a * ⁿ√b + c * ᵐ√d) / (x * ᵏ√y). This multiplication will result in the denominator x * y.
Radical / Sum – (a * √b) / (x * √y + z * √u)
To rationalize the denominator in this case, you need to multiply the expression by the rationalizing factor, which is (x * √y – z * √u) / (x * √y – z * √u). This multiplication will result in the denominator (x * √y)^2 – (z * √u)^2 = xy – zu.
Sum / Sum – (a * √b + c * √d) / (x * √y + z * √u)
Similar to the previous case, you need to multiply the expression by the rationalizing factor, which is (x * √y – z * √u) / (x * √y – z * √u). This multiplication will result in the denominator (x * √y)^2 – (z * √u)^2 = xy – zu.
By using the rationalize the denominator calculator, you can simplify the process of rationalizing the denominator and obtain the simplified result.
Rationalizing Radicals
Rationalizing radicals is an essential concept in algebra that involves eliminating radical expressions from fractions. Radical expressions can include square roots, cube roots, or any other root expressions. By rationalizing radicals, we simplify the expressions and make calculations more manageable.
Rationalizing radicals can be done using various techniques, such as multiplying by the conjugate, using algebraic identities, or applying specific formulas. The choice of method depends on the type of radical expression and the desired outcome.
Why Rationalize a Denominator?
The primary reason for rationalizing a denominator is to simplify calculations involving fractions. Rationalizing the denominator allows us to work with rational numbers, which are easier to manipulate and perform arithmetic operations on. By eliminating radical expressions from the denominator, we obtain a rational denominator, making it more convenient to add, subtract, multiply, or divide fractions.
Rationalizing the denominator also helps in expressing fractions in their simplest form. It allows us to present fractions with a rational denominator, which is generally preferred over fractions with radical denominators. Simplifying fractions by rationalizing the denominator provides a clearer representation and facilitates further mathematical operations.
Solved Examples on Rationalize the Denominator
To better understand the concept of rationalizing the denominator, let’s solve a few examples step by step.
Example 1: Rationalize the denominator of the fraction 3/(2 + √5)
To rationalize the denominator, we multiply both the numerator and the denominator by the conjugate of the denominator, which is 2 – √5.
(3/(2 + √5)) x ((2 – √5)/(2 – √5))
Using the formula (a + b)(a – b) = a^2 – b^2, we simplify the expression:
(3(2 – √5))/((2)^2 – (√5)^2) = (6 – 3√5)/(4 – 5) = (6 – 3√5)/(-1) = -6 + 3√5
By multiplying both the numerator and the denominator by the conjugate of the denominator, we have successfully rationalized the denominator. The fraction is now in its simplest form.
Example 2: Rationalize the denominator of the fraction 1/(4√2)
To rationalize the denominator, we multiply both the numerator and the denominator by √2:
(1/(4√2)) x (√2/√2) = √2/(4√2√2) = √2/(4 x 2) = √2/8 = 1/√8
By multiplying both the numerator and the denominator by √2, we have successfully rationalized the denominator. The fraction is now in its simplest form.
Example 3: Rationalize the denominator of the fraction 1/(√3 + √5)
To rationalize the denominator, we multiply both the numerator and the denominator by the conjugate of the denominator, which is √3 – √5.
(1/(√3 + √5)) x ((√3 – √5)/(√3 – √5)) = (√3 – √5)/(√3√3 – √5√3 + √3√5 – √5√5) = (√3 – √5)/(3 – 5) = (√3 – √5)/(-2) = -√3/2 + √5/2
By multiplying both the numerator and the denominator by the conjugate of the denominator, we have successfully rationalized the denominator. The fraction is now in its simplest form.
How Kunduz Can Help You Learn to Rationalize the Denominator?
If you’re seeking assistance in learning how to rationalize the denominator or any other mathematical concepts, Kunduz is here to help. Kunduz is a comprehensive online learning platform that offers a wide range of courses to enhance your mathematical skills. Whether you’re a student or an adult looking to improve your mathematical understanding, Kunduz provides comprehensive and accessible courses designed to cater to your learning needs.
With Kunduz, you can access step-by-step lessons, practice problems, and real-world examples that will strengthen your understanding of rationalizing the denominator and other mathematical concepts. Our experienced instructors are dedicated to helping you succeed and are available to provide support and guidance throughout your learning journey.
Don’t let the challenges of mathematics hold you back. Join Kunduz today and unlock your full mathematical potential.
