An Introduction to Hyperbolic Function
In mathematics, hyperbolic functions are a set of functions that are analogous to trigonometric functions but are defined using the hyperbola instead of the unit circle. Just as trigonometric functions are defined using the coordinates of points on the unit circle, hyperbolic functions are defined using the coordinates of points on the hyperbola. The six basic hyperbolic functions are sinh (hyperbolic sine), cosh (hyperbolic cosine), tanh (hyperbolic tangent), coth (hyperbolic cotangent), sech (hyperbolic secant), and csch (hyperbolic cosecant).
What is Hyperbolic Function?
Hyperbolic functions are a class of functions that are defined using the exponential function (ex) and its inverse (e-x). These functions are expressed in terms of the coordinates of points on the hyperbola, which allows for the calculation of various mathematical properties. Hyperbolic functions have applications in fields such as geometry, physics, and engineering.

Hyperbolic Definition
Hyperbolic functions are defined using the exponential function and its inverse. The basic hyperbolic functions can be defined as follows:
- sinh x = (ex – e-x)/2
- cosh x = (ex + e-x)/2
- tanh x = sinh x/cosh x
- coth x = cosh x/sinh x
- sech x = 1/cosh x
- csch x = 1/sinh x
These functions are defined for real values of x.
Hyperbolic Functions Formulas
The hyperbolic functions can be expressed using the exponential function. The formulas for the basic hyperbolic functions are as follows:
- sinh x = (ex – e-x)/2
- cosh x = (ex + e-x)/2
- tanh x = sinh x/cosh x
- coth x = cosh x/sinh x
- sech x = 1/cosh x
- csch x = 1/sinh x
These formulas allow for the calculation of the values of the hyperbolic functions for any given value of x.
Hyperbolic Sine Function
The hyperbolic sine function, sinh x, is defined as the difference between the exponential function ex and its inverse e-x, divided by 2. It can be represented as:
sinh x = (ex – e-x)/2
Hyperbolic Cosine Function
The hyperbolic cosine function, cosh x, is defined as the sum of the exponential function ex and its inverse e-x, divided by 2. It can be represented as:
cosh x = (ex + e-x)/2
Hyperbolic Tangent Function
The hyperbolic tangent function, tanh x, is defined as the ratio of the hyperbolic sine function sinh x to the hyperbolic cosine function cosh x. It can be represented as:
tanh x = sinh x/cosh x = (ex – e-x)/(ex + e-x)
Hyperbolic Cotangent Function
The hyperbolic cotangent function, coth x, is defined as the ratio of the hyperbolic cosine function cosh x to the hyperbolic sine function sinh x. It can be represented as:
coth x = cosh x/sinh x = (ex + e-x)/(ex – e-x)
Hyperbolic Secant Function
The hyperbolic secant function, sech x, is defined as the reciprocal of the hyperbolic cosine function cosh x. It can be represented as:
sech x = 1/cosh x = 2/(ex + e-x)
Hyperbolic Cosecant Function
The hyperbolic cosecant function, csch x, is defined as the reciprocal of the hyperbolic sine function sinh x. It can be represented as:
csch x = 1/sinh x = 2/(ex – e-x)
These formulas allow for the calculation of the values of the hyperbolic functions for any given value of x.
Hyperbolic Functions Graphs
The graphs of hyperbolic functions represent the rectangular hyperbola. The graph of the hyperbolic sine function, sinh x, is symmetric with respect to the origin and approaches infinity as x approaches infinity. The graph of the hyperbolic cosine function, cosh x, is also symmetric with respect to the origin and approaches infinity as x approaches infinity. The graph of the hyperbolic tangent function, tanh x, is symmetric with respect to the origin and approaches -1 and 1 as x approaches negative and positive infinity, respectively. The graphs of the other hyperbolic functions have similar characteristics.
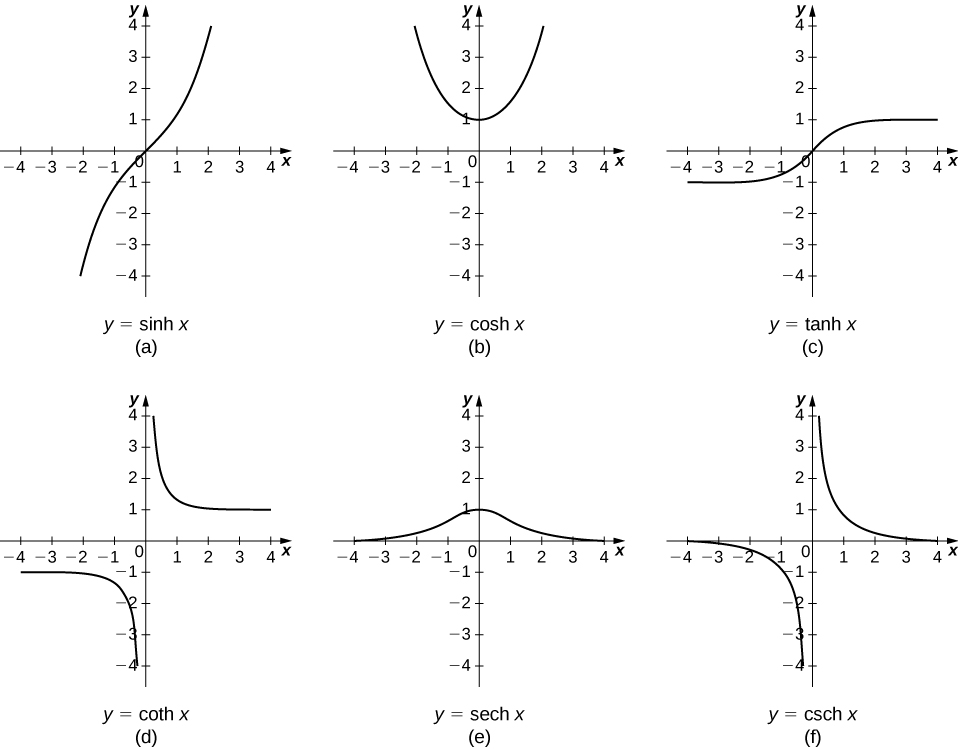
Properties of Hyperbolic Functions
The hyperbolic functions have various properties that are analogous to the properties of trigonometric functions. Some of the important properties of hyperbolic functions are:
- sinh (-x) = -sinh x
- cosh (-x) = cosh x
- sinh 2x = 2 sinh x cosh x
- cosh 2x = cosh^2 x + sinh^2 x
These properties allow for the manipulation and simplification of expressions involving hyperbolic functions.
Domain and Range of Hyperbolic Functions
The domain and range of hyperbolic functions depend on the specific function. The domain of hyperbolic sine and hyperbolic cosine functions is the set of all real numbers, while the range of the hyperbolic sine function is the set of all real numbers and the range of the hyperbolic cosine function is [1, ∞). The domain of the hyperbolic tangent function is the set of all real numbers except for x = ±π/2, ±3π/2, ±5π/2, …, and the range is (-1, 1). The domain of the hyperbolic cotangent function is the set of all real numbers except for x = 0, ±π, ±2π, …, and the range is (-∞, -1) U (1, ∞). The domain of the hyperbolic secant function is the set of all real numbers except for x = ±π/2, ±3π/2, ±5π/2, …, and the range is (0, 1]. The domain of the hyperbolic cosecant function is the set of all real numbers except for x = 0, ±π, ±2π, …, and the range is (-∞, 0) U (0, ∞).
Hyperbolic Function Identities
The hyperbolic function identities are similar to the trigonometric function identities and can be used to simplify expressions involving hyperbolic functions. Some of the important hyperbolic function identities are:
- sinh(-x) = -sinh(x)
- cosh(-x) = cosh(x)
- sinh(x ± y) = sinh(x) cosh(y) ± cosh(x) sinh(y)
- cosh(x ± y) = cosh(x) cosh(y) ± sinh(x) sinh(y)
- tanh(x ± y) = (tanh(x) ± tanh(y)) / (1 ± tanh(x) tanh(y))
- coth(x ± y) = (coth(x) coth(y) ± 1) / (coth(y) ± coth(x))
These identities can be used to simplify and manipulate expressions involving hyperbolic functions.
Hyperbolic Functions Derivatives
The derivatives of hyperbolic functions can be calculated using the rules of differentiation. The derivative of the hyperbolic sine function sinh(x) is the hyperbolic cosine function cosh(x), and the derivative of the hyperbolic cosine function cosh(x) is the hyperbolic sine function sinh(x). The derivatives of the other hyperbolic functions can be obtained using the quotient rule and the chain rule. The derivatives of the hyperbolic functions are:
- d/dx sinh(x) = cosh(x)
- d/dx cosh(x) = sinh(x)
- d/dx tanh(x) = sech^2(x)
- d/dx coth(x) = -csch^2(x)
- d/dx sech(x) = -sech(x) tanh(x)
- d/dx csch(x) = -csch(x) coth(x)
These derivatives can be used to find the rate of change of hyperbolic functions with respect to the independent variable.
Hyperbolic Function Integrals
The integrals of hyperbolic functions can be calculated using the rules of integration. The integral of the hyperbolic sine function sinh(x) is the hyperbolic cosine function cosh(x), and the integral of the hyperbolic cosine function cosh(x) is the hyperbolic sine function sinh(x). The integrals of the other hyperbolic functions can be obtained using integration by substitution and other techniques. The integrals of the hyperbolic functions are:
- ∫ sinh(x) dx = cosh(x) + C
- ∫ cosh(x) dx = sinh(x) + C
- ∫ tanh(x) dx = ln(cosh(x)) + C
- ∫ coth(x) dx = ln(sinh(x)) + C
- ∫ sech(x) dx = arctan(sinh(x)) + C
- ∫ csch(x) dx = ln(tanh(x/2)) + C
These integrals can be used to find the area under the curve of hyperbolic functions and to solve various mathematical problems.
Inverse Hyperbolic Functions
The inverse hyperbolic functions are the inverse functions of the hyperbolic functions. They can be used to find the hyperbolic angle corresponding to a given value of a hyperbolic function. The inverse hyperbolic functions are denoted as sinh^(-1)(x), cosh^(-1)(x), tanh^(-1)(x), coth^(-1)(x), sech^(-1)(x), and csch^(-1)(x). These functions can be used to solve equations involving hyperbolic functions and to find the values of hyperbolic functions for a given hyperbolic angle.
Applications of Hyperbolic Functions
Hyperbolic functions have various applications in mathematics, physics, and engineering. They are used in the calculation of distances and angles in hyperbolic geometry. They also play a role in the solutions of linear differential equations, cubic equations, and Laplace’s equation in Cartesian coordinates. Hyperbolic functions can be used to model the shape of suspension bridges and the behavior of electric circuits. They are also used in the study of fluid dynamics, heat transfer, and electromagnetic theory.
Relationship to the Equations for a Unit Circle
The hyperbolic functions can be related to the equations for a unit circle. While trigonometric functions are defined using the coordinates of points on a unit circle, hyperbolic functions are defined using the coordinates of points on a hyperbola. The equations for a unit circle are x^2 + y^2 = 1, while the equations for a hyperbola are x^2 – y^2 = 1. The hyperbolic functions can be derived from the trigonometric functions by replacing the unit circle with a hyperbola in the equations.
Shape of a Suspension Bridge
The shape of a suspension bridge can be modeled using the hyperbolic functions. The curve of the suspension cable is a catenary, which is a shape described by the hyperbolic cosine function. The equation for a catenary is y = a cosh(x/a), where a is a constant that determines the shape of the curve. The hyperbolic functions can be used to calculate the dimensions and properties of the suspension bridge.
Solved Examples on Hyperbolic Function
Example 1: Find the value of sinh(0)
Solution: The hyperbolic sine function sinh(x) is defined as (ex – e-x)/2. When x = 0, the expression becomes (e0 – e-0)/2 = (1 – 1)/2 = 0. Therefore, sinh(0) = 0.
Example 2: Find the derivative of cosh(x)
Solution: The hyperbolic cosine function cosh(x) is defined as (ex + e-x)/2. To find the derivative, we can use the rules of differentiation. Taking the derivative of cosh(x), we get d/dx cosh(x) = sinh(x). Therefore, the derivative of cosh(x) is sinh(x).
Example 3: Find the integral of tanh(x)
Solution: The hyperbolic tangent function tanh(x) is defined as sinh(x)/cosh(x). To find the integral, we can use the rules of integration. Taking the integral of tanh(x), we get ∫ tanh(x) dx = ln(cosh(x)) + C, where C is the constant of integration. Therefore, the integral of tanh(x) is ln(cosh(x)) + C.
How Kunduz Can Help You Learn Hyperbolic Function?
Kunduz is an online learning platform that offers comprehensive resources and tools for learning hyperbolic functions. With Kunduz, you can access interactive lessons, practice problems, and step-by-step solutions to help you master hyperbolic functions. Our experienced instructors are available to provide personalized guidance and support, ensuring that you have a thorough understanding of the concepts. Whether you are a student studying for an exam or a professional looking to expand your mathematical knowledge, Kunduz can help you achieve your goals. Join Kunduz today and unlock the power of hyperbolic functions.
