In the realm of mathematics, there exists a class of numbers that are not considered “real.” These numbers, known as imaginary numbers, play a crucial role in various mathematical concepts and applications. Despite their name, imaginary numbers are very much real and are used to solve complex equations that involve the square root of negative numbers. In this article, we will explore the definition, rules, operations, and examples of imaginary numbers, as well as the value of “i” in mathematics.
What are Imaginary Numbers?
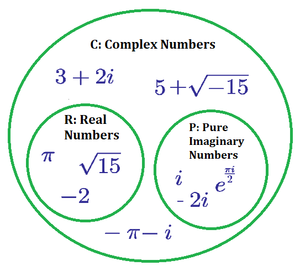
Imaginary numbers are numbers that yield a negative result when squared. They are defined as the square root of negative numbers, which lack a tangible value. Imaginary numbers cannot be represented on a number line, which is why they are called ‘imaginary’. However, they are real in the sense that they are used in mathematics.
These numbers are denoted by the symbol “i”, where i = √(-1). Therefore, an imaginary number is essentially a real number multiplied by “i”. For instance, if you have 3i, “3” is the real number and “i” is the imaginary unit. When 3i is squared, it results in -9, since i² = -1.
Imaginary Number Rules
Several rules govern the operation and manipulation of imaginary numbers. These rules are based on the fundamental principle i = √-1. From this formula, we derive the following key rules:
- i² = -1
- i³ = -i
- i⁴ = 1
These rules are vital in performing algebraic operations on imaginary numbers.
Value of “i” in Math
In mathematics, “i” is known as an imaginary unit whose value is √-1. It is used to compute the square roots of negative numbers. When squared, “i” gives -1, and when cubed, it gives -i.
The multiple of “i” follows a particular cycle. For example:
- i⁴ = 1
- i⁵ = i
- i⁶ = -1
- i⁷ = -i
- i⁸ = 1
This cycle repeats every four multiples, forming a pattern that helps simplify calculations involving powers of “i”.
Algebraic Operations on Imaginary Numbers
Imaginary numbers can be subjected to various algebraic operations, including addition, subtraction, multiplication, and division. Let’s explore each of these operations in detail:
Addition of Numbers Having Imaginary Numbers
When adding two complex numbers a + bi and c + di, we simply add the real parts (a + c) and the imaginary parts (b + d) separately. The result is a complex number of the form (a + c) + (b + d)i.
Example:
(a + bi) + (c + di) = (a + c) + (b + d)i
Subtraction of Numbers Having Imaginary Numbers
Subtracting one complex number (c + di) from another (a + bi) is similar to addition. We subtract the real parts (a – c) and the imaginary parts (b – d) separately to obtain the result in the form (a – c) + (b – d)i.
Example:
(a + bi) - (c + di) = (a - c) + (b - d)i
Multiplication of Numbers Having Imaginary Numbers
Multiplication involves expanding and simplifying the product, taking into account the rules of “i”. For instance, (2 + 3i)(1 – 2i) would be expanded to 2 – 4i + 3i – 6i². Using the rule i² = -1, this simplifies to 2 – i + 6, which equals 8 – i.
Example:
(a + bi) * (c + di) = (ac - bd) + (ad + bc)i
Division of Numbers Having Imaginary Numbers
Dividing one complex number (a + bi) by another (c + di) involves multiplying both the numerator and denominator by the conjugate of the denominator (c – di). This process eliminates the imaginary part in the denominator and simplifies the expression.
Example:
(a + bi) / (c + di) = (a + bi)(c - di) / (c + di)(c - di)
Simplifying Imaginary Numbers
Simplifying imaginary numbers involves expressing them in their simplest form, where the real and imaginary parts are combined. For example, the number 3 + 4i is already in its simplest form, as there are no common factors that can be factored out. However, the number 6 + 8i can be simplified by dividing both the real and imaginary parts by their greatest common factor, which in this case is 2. The simplified form of 6 + 8i is 3 + 4i.
Geometrical Interpretation of Imaginary Numbers
In addition to their algebraic properties, imaginary numbers can also be represented geometrically. In the complex plane, the real part of a complex number is plotted on the horizontal axis, while the imaginary part is plotted on the vertical axis. This representation allows complex numbers, including imaginary numbers, to be visualized as points in a two-dimensional plane. Imaginary numbers, in particular, lie along the vertical axis, as they have no real component.
Principal Square Root of Number
The principal square root of a non-negative real number is the non-negative square root. However, when dealing with negative numbers, the square root is expressed in terms of the imaginary unit “i.” For example, the principal square root of -1 is denoted as √(-1) = i. Similarly, the square root of -4 is expressed as √(-4) = 2i.

Real And Imaginary Numbers
Real numbers and imaginary numbers are distinct but interconnected concepts in mathematics. Real numbers include all rational and irrational numbers, such as integers, fractions, and decimals. Imaginary numbers, on the other hand, involve the square root of negative numbers, which cannot be represented on the real number line. However, both real and imaginary numbers are components of complex numbers, which combine the real and imaginary parts.
Imaginary Numbers Symbol
The symbol for imaginary numbers is “i,” which represents the square root of -1. In mathematical expressions, “i” is multiplied by the coefficient of the imaginary part to form a complex number. For example, in the expression 3 + 4i, the symbol “i” is multiplied by 4 to indicate the imaginary part of the complex number.
Imaginary Numbers Chart
Keeping track of the powers of “i” can be simplified using an imaginary numbers chart. This chart shows the pattern that emerges when “i” is raised to different powers.
| Power of i | Output |
|---|---|
| i¹ | i |
| i² | -1 |
| i³ | -i |
| i⁴ | 1 |
| i⁵ | i |
This pattern repeats every four multiples, which greatly simplifies calculations involving powers of “i”.
Uses of Imaginary Numbers
Imaginary numbers have numerous applications in various fields of mathematics and science. Some of the common uses of imaginary numbers include:
- Complex Analysis: Imaginary numbers play a crucial role in complex analysis, which involves the study of functions that operate on complex numbers. Complex analysis is used in many areas of mathematics, physics, and engineering.
- Electrical Engineering: Imaginary numbers are extensively used in electrical engineering, specifically in the analysis of alternating current (AC) circuits. AC circuits involve complex numbers, and imaginary numbers help represent the phase and impedance of electrical components.
- Signal Processing: Imaginary numbers are used in signal processing to analyze and manipulate signals. Complex numbers, including imaginary numbers, are utilized to represent the frequency and phase of signals in various applications, such as telecommunications and audio processing.
- Quantum Mechanics: In quantum mechanics, imaginary numbers are used to represent the probabilities and amplitudes of quantum states. Complex numbers, including imaginary numbers, are used to describe the behavior of subatomic particles and their interactions.
Solved Examples on Imaginary Numbers
Let’s explore some examples that involve the use of imaginary numbers:
Example 1: Simplify the expression √(-49).
Solution: The square root of -49 can be written as √(-1) * √49. Since √(-1) = i and √49 = 7, the simplification becomes 7i.
Example 2: Simplify and multiply (2i)(3i).
Solution: When multiplying 2i and 3i, we multiply their coefficients and then multiply i by itself. This gives us (23)(ii) = 6(-1) = -6.
Example 3: Simplify the square root of -16.
Solution: The square root of -16 can be simplified as the square root of 16 times the square root of -1 (since -16 = 16*-1). This gives us 4i (since the square root of 16 is 4 and the square root of -1 is i).
How Kunduz Can Help You Learn Imaginary Numbers?
Kunduz, a renowned online learning platform, offers comprehensive resources and materials to help you understand and master the concepts of imaginary numbers. Whether you are a student studying mathematics or a professional in a related field, Kunduz provides step-by-step lessons, practice problems, and interactive tutorials to enhance your understanding of imaginary numbers. With Kunduz, you can learn at your own pace and receive instant feedback to track your progress. Start your journey with Kunduz today and unlock the power of imaginary numbers!
