In the world of mathematics, understanding the rate at which things change is crucial. One important concept in this realm is the instantaneous rate of change. This concept allows us to determine how a function is changing at a specific point, providing us with valuable information about its behavior. By studying the instantaneous rate of change, we can gain insights into various phenomena, from the motion of objects to the growth of populations.
What is Instantaneous Rate of Change?
The instantaneous rate of change refers to the rate at which a quantity is changing at a particular instant. It provides us with the slope of the tangent line to a curve at a specific point. In other words, it measures the rate of change of a function at a precise moment in time or a specific value of the independent variable.
To better understand this concept, let’s consider the example of a car traveling along a road. The average speed of the car over a given interval can provide us with information about its overall motion. However, if we want to know how fast the car is traveling at a specific moment, we need to determine its instantaneous speed. The instantaneous rate of change allows us to do just that.

Instantaneous Rate of Change Formula
The formula for the instantaneous rate of change is derived from the average rate of change formula. It’s represented using limits as follows:
f'(a) = lim(h→0) (f(a+h) - f(a)) / h
Here, f'(a) represents the instantaneous rate of change at x = a, f(a+h) and f(a) are the values of the function at x = a+h and x = a respectively, and h is a small increment in x.
Instantaneous Rate of Change Equation
This equation of the instantaneous rate of change, also known as the derivative of a function, is particularly useful in physics to calculate velocity, acceleration, and other rates of change. It’s also applied in various other fields, such as economics, biology, and engineering, to evaluate changes over time.
Average Rate of Change
The average rate of change of a function over a certain interval is the total change in the dependent variable divided by the total change in the independent variable. It’s calculated using the formula:
Average Rate of Change = (f(x2) - f(x1)) / (x2 - x1)
Where x1 and x2 are two points on the function f(x).
Instantaneous Rate of Change of a Function
The instantaneous rate of change of a function represents the rate at which the function is changing at a specific point. It provides us with information about the slope of the function at that point, indicating whether the function is increasing or decreasing.
To find the instantaneous rate of change of a function, we need to calculate its derivative. The derivative of a function represents its rate of change at any given point. By evaluating the derivative at a specific point, we can determine the instantaneous rate of change of the function at that point.
Derivation of Formula for Instantaneous Rate of Change
The formula for the instantaneous rate of change is obtained by taking the limit as h approaches zero in the average rate of change formula, which results in the derivative of the function. This limit represents the slope of the tangent line to the function at a specific point, providing the instantaneous rate of change at that point.
Derivative Notation
In calculus, different notations are used to represent the derivative of a function. These notations provide us with a concise and standardized way of expressing the derivative.
There are several commonly used notations for the derivative, including Leibniz notation, Newton notation, Lagrange notation, and Euler’s notation.
Leibniz notation
First derivative of y with respect to x: dy/dx
Second derivative of y with respect to x: d²y/dx²
Newton notation
First derivative of y: ẏ
Second derivative of y: ÿ
Lagrange notation
First derivative of y: y'
Second derivative of y: y''
Euler’s notation
First derivative: Dxf
Second derivative: Dx²f
How to Find Instantaneous Rate of Change?
To find the instantaneous rate of change of a function, we need to follow these steps:
- Determine the function: Identify the function for which you want to find the instantaneous rate of change.
- Calculate the derivative: Use the appropriate derivative formula to calculate the derivative of the function.
- Substitute the value: Plug in the desired value of the independent variable at which you want to find the instantaneous rate of change.
- Evaluate the result: Simplify the expression and calculate the value to find the instantaneous rate of change at the specific point.
By following these steps, you can find the instantaneous rate of change of a function at any desired point.
Equation of Instantaneous Rate of Change
The equation of the instantaneous rate of change is given by the derivative of the function. This derivative can be calculated using the limit definition of the derivative, resulting in an equation that describes the rate of change of the function at any given point.
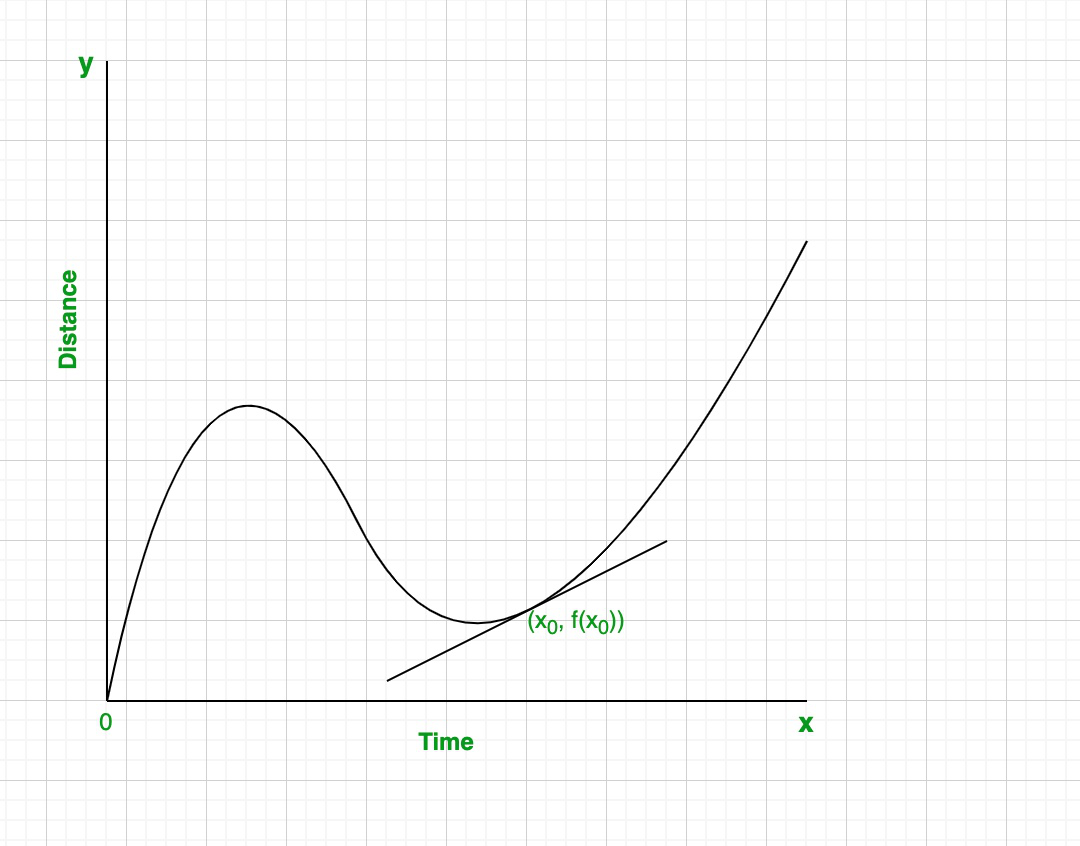
Graphical Representation of Instantaneous Rate of Change
The concept of instantaneous rate of change can also be understood graphically. When graphing a function, the instantaneous rate of change at a specific point is equal to the slope of the tangent line to the graph at that point.
To visualize this concept, consider a graph of a function. The tangent line at a specific point on the graph touches the curve at only one point and represents the instantaneous rate of change at that point.
By examining the slope of the tangent line, we can determine whether the function is increasing or decreasing at that point. A positive slope indicates an increasing function, while a negative slope indicates a decreasing function.
Graphical representation helps us understand the behavior of a function and provides visual evidence of the instantaneous rate of change at specific points.
Frequently Asked Questions on Instantaneous Rate of Change
Is the instantaneous rate of change slope?
Yes, the instantaneous rate of change can be understood as the slope of the tangent line to the graph of a function at a specific point. The slope of the tangent line represents the rate at which the function is changing at that point, providing us with valuable information about its behavior.
How to find the average rate of change between two points using a secant line?
To find the average rate of change between two points using a secant line, you can follow these steps:
- Identify the two points: Determine the coordinates of the two points between which you want to find the average rate of change.
- Draw a secant line: Connect the two points on the graph of the function with a straight line.
- Calculate the slope: Use the coordinates of the two points to calculate the slope of the secant line. The slope represents the average rate of change between the two points.
By following these steps, you can find the average rate of change between two points using a secant line.
How to Calculate Instantaneous Rate of Change in Graph?
To calculate the instantaneous rate of change in a graph, you can follow these steps:
- Draw a tangent line: Draw a straight line that touches the graph of the function at the specific point of interest without crossing over the curve. The tangent line should only touch the graph at that point.
- Calculate the slope: Use the coordinates of any two points on the tangent line to calculate its slope. The slope represents the instantaneous rate of change of the function at the specific point.
By following these steps, you can calculate the instantaneous rate of change in a graph using tangent lines.
Solved Examples on Instantaneous Rate of Change
Let’s solve a few examples to further understand the concept of instantaneous rate of change.
Example 1: Calculate the Instantaneous rate of change of the function (f(x) = 3x² + 12) at (x = 4).
Solution: Given function: (f(x) = 3x² + 12)
To find the instantaneous rate of change, we need to calculate the derivative of the function and evaluate it at (x = 4).
Calculating the derivative of the function: (f'(x) = 6x)
Evaluating the derivative at x = 4: (f'(4) = 6(4)) (f'(4) = 24)
Therefore, the instantaneous rate of change of the function \(f(x) = 3x² + 12\) at \(x = 4\) is 24.
Example 2: Calculate the Instantaneous rate of change of the function (f(x) = 5x³ – 4x² + 2x + 1) at \(x = 2).
Solution: Given function: (f(x) = 5x³ – 4x² + 2x + 1)
To find the instantaneous rate of change, we need to calculate the derivative of the function and evaluate it at (x = 2).
Calculating the derivative of the function: (f'(x) = 15x² – 8x + 2)
Evaluating the derivative at (x = 2): (f'(2) = 15(2)² – 8(2) + 2) (f'(2) = 60 – 16 + 2) (f'(2) = 46)
Therefore, the instantaneous rate of change of the function (f(x) = 5x³ – 4x² + 2x + 1) at (x = 2) is 46.
How Kunduz Can Help You Learn Instantaneous Rate of Change?
Kunduz is your trusted companion in the realm of mathematics and its various concepts, including the instantaneous rate of change. With our comprehensive learning resources and expert guidance, you can master this concept and excel in your mathematical pursuits.
We offer a wide range of educational materials, including interactive videos, practice exercises, and step-by-step tutorials, designed to cater to different learning styles and levels of understanding. Whether you are a beginner or an advanced learner, Kunduz has resources tailored to your needs.
By joining Kunduz, you gain access to a supportive community of fellow learners and experienced instructors who are passionate about mathematics. Our platform is user-friendly and accessible, allowing you to learn at your own pace and from the comfort of your own home.
Don’t let the complexities of mathematics intimidate you. With Kunduz, you have the tools and support you need to conquer the world of instantaneous rate of change and beyond. Start your learning journey with Kunduz today and unlock a world of mathematical possibilities.
