In geometry, the concept of angles is fundamental to understanding the properties of shapes. When it comes to polygons, which are closed figures with straight sides, one important aspect to consider is the interior angles. These angles are formed by the intersection of two adjacent sides of a polygon at a common point, known as the vertex. The study of interior angles is crucial for analyzing the properties and relationships of polygons.
What are the Interior Angles?
Interior angles are the angles formed inside a polygon. They are the angles that lie between two adjacent sides of a polygon. Each polygon has a unique number of interior angles, which is equal to the number of sides of the polygon. For example, a triangle, which has three sides, will have three interior angles. The sum of the interior angles of a polygon is always constant, regardless of the size or shape of the polygon.
Types of Interior Angles
There are two types of interior angles that are commonly studied: alternate interior angles and co-interior angles.
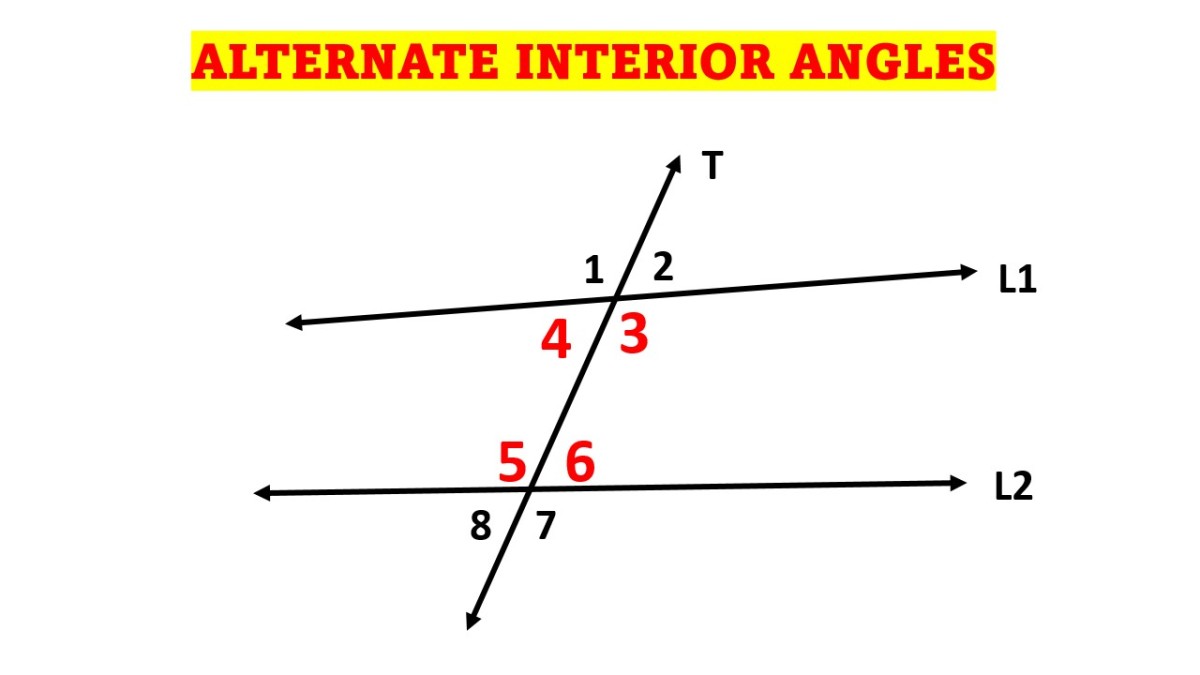
Alternate Interior Angles
Alternate interior angles are formed when two parallel lines are intersected by a transversal. These angles are located on opposite sides of the transversal and between the two parallel lines. The key property of alternate interior angles is that they are congruent, meaning they have the same measure. This property holds true regardless of the angle’s size or shape.
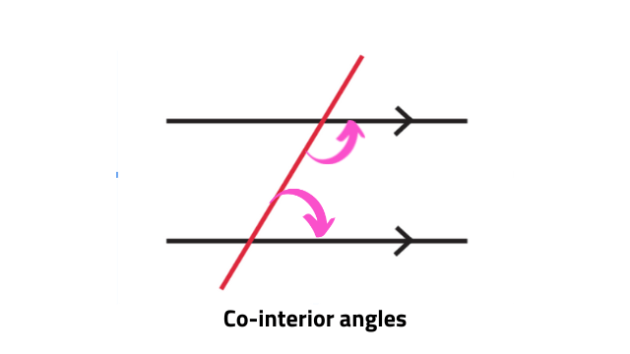
Co-Interior Angles
Co-interior angles, also known as same-side interior angles or consecutive interior angles, are formed when two parallel lines are intersected by a transversal. These angles are located on the same side of the transversal and between the two parallel lines. The sum of co-interior angles is always 180 degrees, making them supplementary angles.
Classification of Triangles Based on Interior Angles
Triangles, which are polygons with three sides, can be classified based on the measurements of their interior angles. The classification includes acute triangles, obtuse triangles, and right triangles.
Acute Triangle
An acute triangle is a triangle in which all three interior angles are acute angles, meaning they measure less than 90 degrees. In an acute triangle, the sum of the interior angles is always 180 degrees.
Obtuse Triangle
An obtuse triangle is a triangle in which one of the interior angles is an obtuse angle, measuring more than 90 degrees. The other two interior angles are acute angles. The sum of the interior angles in an obtuse triangle is also 180 degrees.
Right Triangle
A right triangle is a triangle in which one of the interior angles is a right angle, measuring exactly 90 degrees. The other two interior angles are acute angles. The sum of the interior angles in a right triangle is still 180 degrees.
Sum of Interior Angles Formula
The sum of the interior angles of a polygon can be calculated using a formula. The formula states that the sum of the interior angles of a polygon with ‘n’ sides is equal to (n-2) multiplied by 180 degrees. This formula holds true for all polygons, regardless of their size or shape.
For example, let’s consider a triangle, which has three sides. Using the formula, we can calculate the sum of its interior angles:
Sum of Interior Angles of a Triangle = (3-2) * 180 degrees = 180 degrees
Similarly, for a quadrilateral with four sides:
Sum of Interior Angles of a Quadrilateral = (4-2) * 180 degrees = 360 degrees
This formula can be applied to any polygon to determine the sum of its interior angles.
Finding an Unknown Interior Angle
Sometimes, we might need to find the measure of an unknown interior angle of a polygon. To do this, we can use the sum of interior angles formula and the given information about the polygon. By subtracting the sum of the known interior angles from the total sum of interior angles, we can find the measure of the unknown angle.
For example, let’s say we have a hexagon with known interior angles of 140 degrees, 120 degrees, 150 degrees, 130 degrees, and 90 degrees. The sum of the interior angles of a hexagon is 720 degrees. We can find the measure of the unknown angle by subtracting the sum of the known angles from the total sum of interior angles:
Unknown Angle = 720 degrees – (140 degrees + 120 degrees + 150 degrees + 130 degrees + 90 degrees) Unknown Angle = 720 degrees – 630 degrees Unknown Angle = 90 degrees
Therefore, the measure of the unknown angle is 90 degrees.
Interior Angles of Polygons
The interior angles of polygons can vary depending on the number of sides they have. Here is a table that shows the number of sides, the sum of interior angles, and the measurement of each interior angle for polygons with different numbers of sides:
| Polygon | Number of Sides (n) | Sum of Interior Angles | Measurement of Each Interior Angle |
|---|---|---|---|
| Triangle | 3 | 180 degrees | 60 degrees |
| Quadrilateral | 4 | 360 degrees | 90 degrees |
| Pentagon | 5 | 540 degrees | 108 degrees |
| Hexagon | 6 | 720 degrees | 120 degrees |
| Heptagon/Septagon | 7 | 900 degrees | 128.57 degrees |
| Octagon | 8 | 1080 degrees | 135 degrees |
| Nonagon | 9 | 1260 degrees | 140 degrees |
| Decagon | 10 | 1440 degrees | 144 degrees |
As the number of sides increases, the sum of the interior angles of a polygon also increases, while the measurement of each interior angle decreases.
Interior Angles Theorem
The Interior Angles Theorem states that the sum of the interior angles of a polygon is equal to (2n – 4) times 90 degrees, where ‘n’ is the number of sides of the polygon. This theorem allows us to calculate the sum of the interior angles without individually measuring each angle.
For example, let’s consider a pentagon, which has five sides. Using the Interior Angles Theorem, we can calculate the sum of its interior angles:
Sum of Interior Angles of a Pentagon = (2 * 5 – 4) * 90 degrees = 540 degrees
This theorem can be applied to any polygon to determine the sum of its interior angles.
Interior Angles vs. Exterior Angles
Interior angles and exterior angles are two types of angles associated with polygons. Interior angles are formed inside the polygon, while exterior angles are formed outside the polygon. The sum of an interior angle and its corresponding exterior angle is always 180 degrees.
For example, in a regular polygon, each interior angle is congruent to the other interior angles, and each exterior angle is also congruent to the other exterior angles. The sum of an interior angle and its corresponding exterior angle is always 180 degrees.
Solved Examples on Interior Angles
Let’s solve a few examples to better understand the concept of interior angles:
Example 1: Find the measure of each interior angle of a regular hexagon.
Solution: A regular hexagon has six sides. Using the formula for the measurement of each interior angle of a regular polygon, we can calculate the measure of each interior angle of the hexagon:
Measurement of Each Interior Angle = (180 * (6-2))/6 degrees = (180 * 4)/6 degrees = 120 degrees
Therefore, each interior angle of a regular hexagon measures 120 degrees.
Example 2: Find the sum of the interior angles of a decagon.
Solution: A decagon has ten sides. Using the formula for the sum of the interior angles of a polygon, we can calculate the sum of the interior angles of the decagon:
Sum of Interior Angles = (10-2) * 180 degrees = 8 * 180 degrees = 1440 degrees
Therefore, the sum of the interior angles of a decagon is 1440 degrees.
Example 3: If a regular polygon has each interior angle measuring 120°, how many sides does this polygon have?
Solution: We know that the sum of each interior angle and its corresponding exterior angle is 180°. So, the exterior angle is 180° – 120° = 60°.
The formula to find the number of sides of a regular polygon is:
Number of Sides of a Regular Polygon = 360° / Magnitude of each exterior angle
So, the number of sides = 360° / 60° = 6 sides.
Therefore, this regular polygon is a hexagon.
How Kunduz Can Help You Learn Interior Angles?
Kunduz is a comprehensive online learning platform that provides a wide range of educational resources to help students excel in their studies. Whether you need assistance with understanding interior angles or any other mathematical concept, Kunduz offers expertly designed lessons, engaging videos, interactive quizzes, and personalized learning plans to cater to your individual needs.
With Kunduz, you can learn at your own pace, access educational materials anytime and anywhere, and receive immediate feedback to track your progress. The platform also provides various instructional tools and resources to make learning math enjoyable and effective.
By utilizing Kunduz’s user-friendly interface, step-by-step explanations, and interactive learning features, you can strengthen your understanding of interior angles and enhance your problem-solving skills. Kunduz is your trusted companion in achieving academic success in mathematics. Start your learning journey with Kunduz today!
