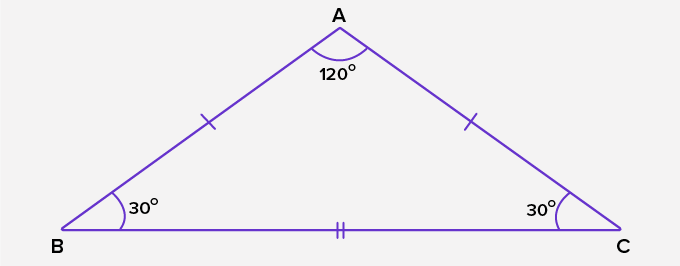
In the realm of geometry, triangles are fundamental shapes that come in various forms. One such type is the isosceles triangle. Defined by its two equal sides and one unequal side, the isosceles triangle holds a unique place among its geometric counterparts. Understanding its properties, angles, formulas, and types is essential for a comprehensive knowledge of triangles.
In this article, we will delve into the world of the isosceles triangle, exploring its definition, properties, angles, types, and various formulas associated with it. We will also provide solved examples to illustrate the practical application of concepts. So, let’s embark on this geometric journey and explore the fascinating world of the isosceles triangle.
What is the Isosceles Triangle?
An isosceles triangle is a triangle that possesses two sides of equal length. This distinctive feature sets it apart from other triangles. While all triangles have three angles, an isosceles triangle specifically contains two angles of equal measure. The third angle, opposite the unequal side, may vary in measurement.
To visualize an isosceles triangle, imagine a triangle with two sides of equal length and one side that is shorter or longer. This triangle may appear symmetrical or asymmetrical depending on the lengths of its sides. The equal sides are often referred to as the “legs” of the triangle, while the unequal side is known as the “base.”
It is important to note that an equilateral triangle, which has all three sides of equal length, is also considered an isosceles triangle. However, not all isosceles triangles are equilateral triangles.

Properties of Isosceles Triangle
Isosceles triangles possess several unique properties that distinguish them from other types of triangles. Understanding these properties is crucial for a comprehensive understanding of the isosceles triangle. Let’s explore some of these properties:
- Two Equal Sides: The defining characteristic of an isosceles triangle is that it has two sides of equal length. These sides are commonly referred to as the “legs” of the triangle.
- One Unequal Side: In addition to the two equal sides, an isosceles triangle also has one side of unequal length. This side is known as the “base” of the triangle.
- Equal Angles: The angles opposite the equal sides of an isosceles triangle are congruent, or equal, in measure. These angles are often referred to as the “base angles” of the triangle.
- Acute Angles: All angles in an isosceles triangle are acute angles, meaning they measure less than 90 degrees. This is because the sum of the angles in any triangle is always 180 degrees.
- Line of Symmetry: The perpendicular bisector drawn from the apex angle, which is the angle between the legs, bisects the base of the isosceles triangle. This line of symmetry divides the triangle into two congruent triangles.
These properties collectively define the unique characteristics of an isosceles triangle, setting it apart from other types of triangles.
Angles of Isosceles Triangle
In an isosceles triangle, the angles play a significant role in defining its shape and properties. Understanding the angles of an isosceles triangle is essential for solving problems and determining various measurements. Let’s explore the angles associated with the isosceles triangle in more detail.
- Vertex Angle: The vertex angle of an isosceles triangle is the angle formed by the two equal sides, also known as the legs of the triangle. This angle is opposite the base of the triangle.
- Base Angles: The base angles of an isosceles triangle are the two angles formed by the base and each of the legs. Since the legs are of equal length, the base angles are also congruent in measure.
The sum of the three angles in any triangle is always 180 degrees. In an isosceles triangle, where two angles are equal, the third angle can be determined by subtracting the sum of the two equal angles from 180 degrees.
Understanding and utilizing the properties and measurements of the angles in an isosceles triangle is essential for solving problems and applying geometric principles.
Isosceles Triangle Theorem And Proof
The Isosceles Triangle Theorem plays a crucial role in understanding the relationships between the sides and angles of an isosceles triangle. This theorem states that if two sides of a triangle are congruent, then the angles opposite those sides are also congruent.
Conversely, if the two angles of a triangle are congruent, then the sides opposite those angles are also congruent. This theorem provides a fundamental relationship between the sides and angles of an isosceles triangle, allowing for the determination of unknown measurements.
To prove the Isosceles Triangle Theorem, we can use various geometric principles and properties. One approach involves drawing a line that bisects the base angle of the isosceles triangle, creating two congruent triangles. This can be proven using the Side-Angle-Side (SAS) congruence criterion.
By demonstrating the congruence of the two triangles formed by the bisector, we can conclude that the sides opposite the equal angles are congruent. This proof solidifies the relationship between the sides and angles in an isosceles triangle, providing a powerful tool for solving geometric problems.
Understanding the Isosceles Triangle Theorem and its proof is essential for applying geometric principles and solving problems related to isosceles triangles.
Types of Isosceles Triangle
Isosceles triangles can be further categorized into different types based on the measurements and relationships of their angles. Let’s explore the three main types of isosceles triangles:
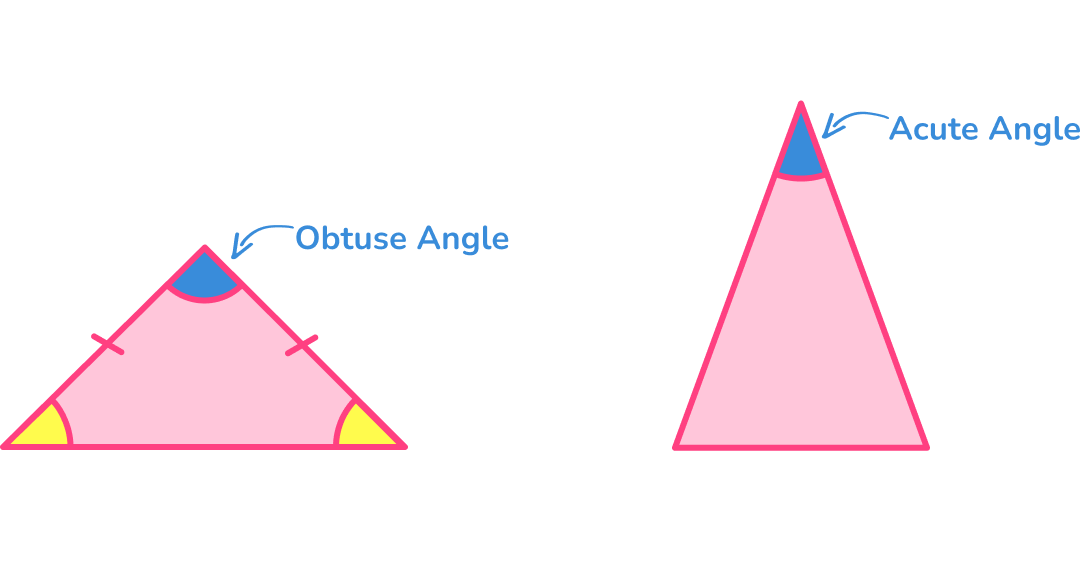
- Isosceles Acute Triangle: An isosceles acute triangle is a triangle in which all three angles are acute, meaning they measure less than 90 degrees. In this type of isosceles triangle, the two equal angles and the third angle are all acute.
- Isosceles Right Triangle: An isosceles right triangle is a triangle that has one right angle, which measures 90 degrees. The other two angles, which are opposite the equal sides, are acute and congruent.
- Isosceles Obtuse Triangle: An isosceles obtuse triangle is a triangle that has one obtuse angle, meaning it measures more than 90 degrees. The other two angles, opposite the equal sides, are acute and congruent.
Understanding the different types of isosceles triangles allows for a more comprehensive understanding of their characteristics and properties. It enables us to apply specific geometric principles and formulas based on the type of isosceles triangle we are dealing with.
Parts of an Isosceles Triangle
To better understand the structure of an isosceles triangle, let’s explore its various components or parts. Familiarizing ourselves with these parts is crucial for solving problems and applying geometric principles. Here are the main parts of an isosceles triangle:
- Legs: The legs of an isosceles triangle are the two equal sides. These sides are adjacent to the vertex angle and opposite the base. The legs are often denoted as “a” in mathematical equations and formulas.
- Base: The base of an isosceles triangle is the unequal side. It is the side opposite the vertex angle and connects the two legs. The base is often denoted as “b” in mathematical equations and formulas.
- Vertex Angle: The vertex angle of an isosceles triangle is formed by the two legs. It is the angle between the two equal sides and is opposite the base of the triangle. The vertex angle is often denoted as “θ” or “alpha” in mathematical equations and formulas.
- Base Angles: The base angles of an isosceles triangle are the two angles formed by the base and each of the legs. These angles are congruent, meaning they have the same measure. The base angles are often denoted as “β” or “gamma” in mathematical equations and formulas.
Understanding the different parts of an isosceles triangle allows us to apply specific formulas and principles to solve problems and determine various measurements.
Finding the Size of Angles in Isosceles Triangles
Determining the measurements of angles in an isosceles triangle is crucial for solving geometric problems and applying mathematical principles. The fact that an isosceles triangle has two congruent angles simplifies the process of finding angle measurements. Let’s explore the different methods for finding the size of angles in isosceles triangles:
- Vertex Angle: The vertex angle, which is formed by the two equal sides of an isosceles triangle, can be found by subtracting the sum of the other two angles from 180 degrees. Since the other two angles are congruent, we can divide this difference by 2 to obtain the measure of the vertex angle.
- Base Angles: The base angles of an isosceles triangle are congruent, meaning they have the same measure. To find the size of the base angles, we can subtract the measure of the vertex angle from 180 degrees and divide this difference by 2.
By employing these methods, we can determine the measurements of the angles in an isosceles triangle. This knowledge is essential for solving geometric problems and applying mathematical principles in various contexts.
Isosceles Triangle Lines of Symmetry
The concept of symmetry plays a significant role in geometry, and isosceles triangles are no exception. Isosceles triangles possess lines of symmetry that divide the triangle into congruent parts. Understanding these lines of symmetry is crucial for identifying symmetrical properties and solving geometric problems. Let’s explore the lines of symmetry in isosceles triangles:
- Perpendicular Bisector: The perpendicular bisector drawn from the apex angle of an isosceles triangle bisects the base. This perpendicular bisector acts as a line of symmetry, dividing the triangle into two congruent triangles.
- Line of Symmetry: The line of symmetry in an isosceles triangle is the line that passes through the midpoint of the base and is perpendicular to the base. This line divides the triangle into two congruent parts, mirroring each other.
Understanding the lines of symmetry in an isosceles triangle allows us to identify congruent parts and apply symmetrical properties when solving geometric problems. It enhances our ability to visualize and analyze the triangle’s structure and properties.
Isosceles Triangle Formulas
Formulas play a crucial role in geometry, providing a systematic approach to solving problems and determining various measurements. Isosceles triangles have specific formulas that allow us to calculate their area, perimeter, and other related quantities. Let’s explore the main formulas associated with isosceles triangles:
- Perimeter of Isosceles Triangle: The perimeter of an isosceles triangle is the sum of the lengths of its three sides. In the case of an isosceles triangle, where two sides are equal, the perimeter can be calculated using the formula: Perimeter = 2 * Side Length + Base Length.
- Area of Isosceles Triangle: The area of an isosceles triangle is the measure of the region enclosed by its three sides. To calculate the area, we can use the formula: Area = (Base Length * Height) / 2. The height is the perpendicular distance from the base to the vertex angle.
- Altitude of Isosceles Triangle: The altitude of an isosceles triangle is the perpendicular distance from the base to the vertex angle. It can be calculated using the formula: Altitude = √(Leg Length^2 – (Base Length/2)^2).
These formulas provide a systematic approach to solving problems related to isosceles triangles, allowing us to determine their perimeter, area, and other important measurements.
Area of Isosceles Triangle
The area of an isosceles triangle is a fundamental quantity that represents the region enclosed by its three sides. Calculating the area of an isosceles triangle requires knowledge of its base length and height like the area of a triangle. Let’s explore the formula and steps to find the area of an isosceles triangle:
Formula: The area of an isosceles triangle can be calculated using the formula: Area = (Base Length * Height) / 2.
Steps to Find the Area of an Isosceles Triangle:
- Identify the base length: The base of an isosceles triangle is the unequal side. Measure or determine the length of the base.
- Determine the height: The height of an isosceles triangle is the perpendicular distance from the base to the vertex angle. Measure or determine the height of the triangle using appropriate methods, such as perpendicular bisector or trigonometry.
- Plug the values into the formula: Once you have the base length and height, substitute these values into the formula for the area of an isosceles triangle: Area = (Base Length * Height) / 2.
- Calculate the area: Use the formula to calculate the area of the isosceles triangle. Make sure to perform the necessary calculations accurately to obtain the correct result.
By following these steps and utilizing the formula, you can find the area of any given isosceles triangle. This measurement is crucial for various geometric applications and problem-solving.
Perimeter of Isosceles Triangle
The perimeter of an isosceles triangle is the total length of its three sides. Calculating the perimeter allows us to determine the distance around the triangle. To find the perimeter of an isosceles triangle, we need to know the lengths of its two equal sides and the base. Let’s explore the formula and steps to find the perimeter of an isosceles triangle:
Formula: The perimeter of an isosceles triangle can be calculated using the formula: Perimeter = 2 * Side Length + Base Length.
Steps to Find the Perimeter of an Isosceles Triangle:
- Identify the side lengths: In an isosceles triangle, two sides are equal in length. Measure or determine the length of one of the equal sides, denoted as “a”. Similarly, measure or determine the length of the base, denoted as “b”.
- Plug the values into the formula: Once you have the side length and base length, substitute these values into the formula for the perimeter of an isosceles triangle: Perimeter = 2 * Side Length + Base Length.
- Perform the calculations: Multiply the side length by 2, and then add the base length to obtain the perimeter of the isosceles triangle. Make sure to perform the necessary calculations accurately to obtain the correct result.
By following these steps and utilizing the formula, you can find the perimeter of any given isosceles triangle. This measurement is essential for various geometric applications and problem-solving.
Isosceles Triangle Altitude
The altitude of an isosceles triangle is the perpendicular distance from the base to the vertex angle. It plays a crucial role in determining various measurements and properties of the triangle. Let’s explore the concept of altitude in an isosceles triangle and how to calculate it:
The altitude of an isosceles triangle can be calculated using the Pythagorean theorem. The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
To calculate the altitude of an isosceles triangle, we need to know the lengths of the equal sides (legs) and the base. The altitude divides the base into two equal segments and forms two right triangles. The length of the altitude can be determined using the following formula:
Altitude = √(Leg Length^2 – (Base Length/2)^2)
By substituting the appropriate values into this formula, you can calculate the altitude of an isosceles triangle. The altitude is a crucial measurement for determining the area of the triangle and understanding its geometric properties.
Scalene, Equilateral, and Isosceles Triangle
Triangles come in various forms, each with its own distinct properties and characteristics. The three common types of triangles are scalene, equilateral, and isosceles triangles. While isosceles triangles have two equal sides, scalene triangles have no equal sides, and equilateral triangles have all sides equal. Let’s explore the differences and similarities between these types of triangles:
- Scalene Triangle: A scalene triangle is a triangle in which all three sides have different lengths. None of the angles in a scalene triangle are equal. Each angle can have a different measurement, making the scalene triangle the most versatile among the three types.
- Equilateral Triangle: An equilateral triangle is a triangle in which all three sides have the same length. Equilateral triangles have three equal angles, each measuring 60 degrees. The equilateral triangle is a special case of an isosceles triangle, where all sides are equal.
- Isosceles Triangle: An isosceles triangle is a triangle that has two equal sides and two equal angles. The angles opposite the equal sides are also equal. The base angles of an isosceles triangle are congruent, while the third angle may vary in measurement. Equilateral triangles are a subset of isosceles triangles.
Although these three types of triangles have distinct characteristics, they share some similarities. All three types are classified as polygons with three sides and three angles. The sum of the interior angles of any triangle is always 180 degrees.
Understanding the differences and similarities between these types of triangles allows us to classify and analyze triangles based on their properties and measurements.
Converse of Isosceles Triangle Theorem
The converse of the Isosceles Triangle Theorem is an important concept in geometry that establishes a relationship between the sides and angles of a triangle. While the Isosceles Triangle Theorem states that if two sides of a triangle are congruent, then the angles opposite those sides are also congruent, the converse states the opposite. The converse of the Isosceles Triangle Theorem states that if two angles of a triangle are congruent, then the sides opposite those angles are also congruent.
This converse theorem provides a useful tool for identifying congruent sides in a triangle based on the congruence of its angles. By observing the equality of two angles, we can conclude that the sides opposite those angles are also equal in length.
The converse of the Isosceles Triangle Theorem is a powerful tool for solving geometric problems and establishing congruence between sides and angles in a triangle. It enables us to make deductions and draw conclusions based on the relationships between the various elements of a triangle.
Understanding and utilizing the converse of the Isosceles Triangle Theorem expands our geometric reasoning and problem-solving abilities, allowing us to apply mathematical principles effectively.
Criteria, Scalene Triangle, Isosceles Triangle, Equilateral Triangle (Table)
Triangles can be classified into various categories based on the lengths of their sides and the measures of their angles. The three main types of triangles are scalene, isosceles, and equilateral triangles. Each type possesses unique properties and characteristics. Let’s explore the criteria and distinguishing features of these types of triangles:
| Criteria | Scalene Triangle | Isosceles Triangle | Equilateral Triangle |
|---|---|---|---|
| Sides | All three sides are unequal. | Two sides are equal. | All three sides are equal. |
| Angles | All three angles are different. | Two angles are equal. | All three angles are equal (60 degrees each). |
| Symmetry | No lines of symmetry. | One line of symmetry (perpendicular bisector of the base). | Three lines of symmetry (passing through each vertex and bisecting the opposite side). |
| Special Property | No congruent sides or angles. | Base angles are congruent. | All sides and angles are congruent. |
| Example | Triangle with side lengths 3, 4, and 5 units. | Triangle with side lengths 5, 5, and 7 units. | Triangle with side lengths 6, 6, and 6 units. |
Understanding the criteria and distinctions between scalene, isosceles, and equilateral triangles helps us classify and analyze different types of triangles based on their properties and measurements. It allows us to apply specific formulas and principles tailored to each type of triangle.
Frequently Asked Questions About Isosceles Triangle
Understanding the properties and characteristics of an isosceles triangle can raise questions and spark curiosity. Let’s explore some frequently asked questions about the isosceles triangle to deepen our understanding:
Do Isosceles Triangles Have Equal Angles?
In an isosceles triangle, the angles opposite the equal sides are congruent or equal in measure. However, the third angle, opposite the unequal side, may vary in measurement.
Can Isosceles Triangles Be Right?
Yes, isosceles triangles can be right triangles if one of the angles measures 90 degrees. In a right isosceles triangle, one of the equal sides forms the right angle, and the other two angles are acute and congruent.
What is the Vertex Angle of an Isosceles Triangle?
The vertex angle of an isosceles triangle is the angle formed by the two equal sides. It is opposite the base of the triangle.
What is the Base of an Isosceles Triangle?
The base of an isosceles triangle is the side that is unequal in length. It is opposite the vertex angle and connects the two equal sides.
What is always true about the angles of an isosceles triangle?
In an isosceles triangle, the angles opposite the equal sides are congruent or equal in measure. The base angles are also congruent.
How many equal sides does an isosceles triangle have?
An isosceles triangle has two equal sides, also known as the legs. The third side, known as the base, is unequal in length.
Exploring these frequently asked questions provides further insight into the properties and characteristics of isosceles triangles. It allows us to address common queries and deepen our understanding of this geometric shape.
Solved Examples on Isosceles Triangle
Solved examples provide practical applications of the concepts and formulas associated with isosceles triangles. Let’s explore a few solved examples to illustrate how to apply these principles in real-world scenarios:
Example 1: Find the area of an isosceles triangle with a base length of 8 units and a height of 6 units.
Solution: The formula for the area of an isosceles triangle is: Area = (Base Length * Height) / 2. Substituting the given values into the formula, we have: Area = (8 * 6) / 2 = 24 square units.
Therefore, the area of the isosceles triangle is 24 square units.
Example 2: In an isosceles triangle, the base angles each measure 50 degrees. What is the measure of the vertex angle?
Solution: Since the base angles of an isosceles triangle are congruent, and each measures 50 degrees, we can use the fact that the sum of the angles in a triangle is 180 degrees. Let the measure of the vertex angle be “x.” The sum of the three angles is: x + 50 + 50 = 180. Combining like terms, we have: x + 100 = 180. Solving for “x,” we subtract 100 from both sides: x = 80.
Therefore, the measure of the vertex angle in the isosceles triangle is 80 degrees.
These solved examples demonstrate how to apply formulas, principles, and concepts related to isosceles triangles in practical scenarios. By understanding these examples, we can develop problem-solving skills and apply geometric principles effectively.
How Kunduz Can Help You Learn Isosceles Triangle?
At Kunduz, we understand the importance of a comprehensive learning experience. We provide a variety of resources and tools to assist you in mastering the concepts and principles related to isosceles triangles. Our platform offers interactive lessons, practice problems, and step-by-step solutions to help you deepen your understanding and enhance your problem-solving skills.
Whether you are a student, teacher, or geometry enthusiast, Kunduz is here to support your learning journey. Our user-friendly interface, engaging content, and comprehensive resources make learning about isosceles triangles an enjoyable and rewarding experience.
Explore our platform today and unlock the power of knowledge in the realm of isosceles triangles. Let Kunduz be your trusted companion on your geometric exploration, and together, we’ll conquer the world of triangles.
In conclusion, the isosceles triangle is a fascinating geometric shape with unique properties and characteristics. Understanding its definition, properties, angles, formulas, and types allows us to apply geometric principles effectively. By exploring examples and utilizing resources like Kunduz, we can deepen our understanding and enhance our problem-solving skills in relation to isosceles triangles. So, let’s embrace the world of triangles and embark on a journey of learning and exploration.