Welcome to this comprehensive guide on linear interpolation! In this article, we will explore the concept of interpolation, with a specific focus on linear interpolation. We will delve into the definition of interpolation, understand what linear interpolation is, and learn about the derivation of the linear interpolation formula. Additionally, we will explore various applications of linear interpolation and provide solved examples to deepen our understanding. So, let’s dive in!
An Introduction to Linear Interpolation
Interpolation is a mathematical technique used to estimate the value of a function between two known values. It allows us to fill in the gaps or predict unknown values based on the existing data points. Linear interpolation, specifically, is a method of curve fitting using linear polynomials. It involves constructing new data points within the range of a discrete set of known data points.
What is Interpolation?
Interpolation is a mathematical method used to estimate the value of a function between two known values. It is particularly useful when we have a set of data points and need to find values that lie between them. By connecting the known data points, interpolation allows us to approximate the value of the function at any desired coordinate. It is commonly used in various fields such as mathematics, physics, engineering, and finance.
:max_bytes(150000):strip_icc()/Interpolation_example_polynomia-17f3432d98424155a2923472c95ae75f.png)
What is Linear Interpolation?
Linear interpolation is a specific type of interpolation that uses linear polynomials to estimate values between known data points. It assumes a linear relationship between the data points and constructs a straight line connecting them. This line is then used to predict the value at any intermediate point.
Linear interpolation is often referred to as “filling in the gaps” for tabular data values. It is a simple and widely used method for estimating unknown values within a given range. However, it is important to note that linear interpolation may not be accurate for non-linear data.
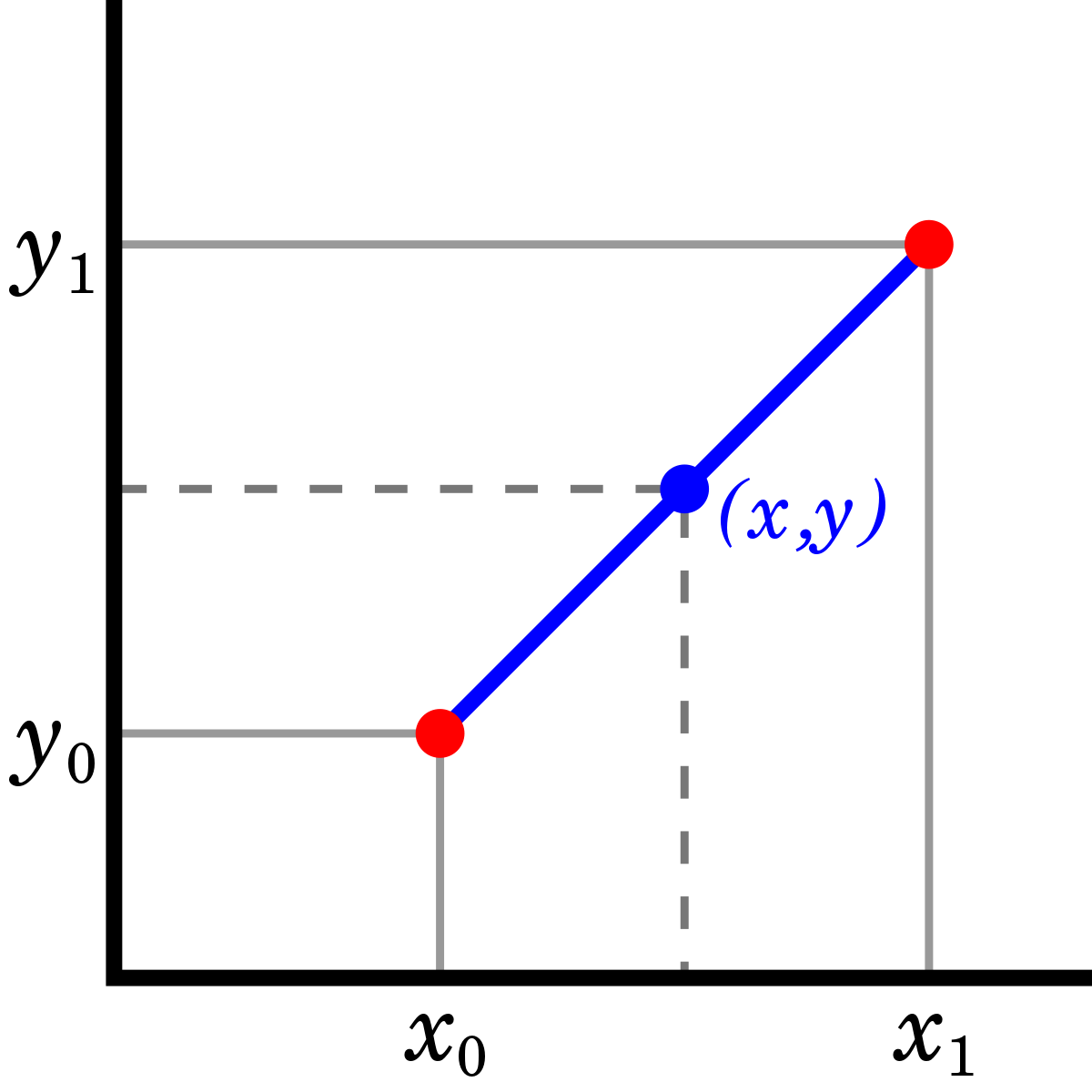
Linear Interpolation Formula
The linear interpolation formula is a mathematical expression that allows us to calculate the estimated value of a function between two known data points. The formula is derived based on the assumption of a linear relationship between the data points. The linear interpolation formula is as follows:
y = y1 + (x – x1) * (y2 – y1) / (x2 – x1)
In this formula,
- x1 and y1 represent the coordinates of the first data point,
- x2 and y2 represent the coordinates of the second data point,
- x is the point at which we want to perform the interpolation, and
- y is the interpolated value.
The formula calculates the interpolated value by determining the proportional difference between the known data points and applying it to the difference between the x-coordinates.
You can also study our slope formula and slope intercept formula.
Linear Interpolation Equation
The linear interpolation equation is a specific form of the linear interpolation formula. It represents the relationship between the known data points and the interpolated value. The linear interpolation equation is derived by rearranging the linear interpolation formula:
y = y1 + (x – x1) * (y2 – y1) / (x2 – x1)
Let’s break down the components of the linear interpolation equation:
- y: The interpolated value.
- y1: The y-coordinate of the first data point.
- x1: The x-coordinate of the first data point.
- x: The point at which we want to perform the interpolation.
- y2: The y-coordinate of the second data point.
- x2: The x-coordinate of the second data point.
By substituting the known values into the equation, we can calculate the interpolated value of y at a specific x-coordinate.
Applications of Linear Interpolation Formula
The linear interpolation formula finds applications in various fields and industries. It is particularly useful in the following scenarios:
- Data Forecasting: Linear interpolation is commonly used to predict future data points based on a trend observed in known data points. It allows us to estimate values between existing data points and make informed forecasts.
- Data Prediction: Linear interpolation is useful in predicting missing values in a dataset. By using known data points, we can estimate the values that are not available, filling in the gaps and completing the dataset.
- Market Research: Linear interpolation is employed in market research to estimate values between known data points. It enables researchers to infer consumer preferences, market trends, and forecast future market conditions.
- Mathematical and Scientific Applications: Linear interpolation is extensively used in mathematical and scientific fields for various purposes. It aids in approximating complex functions, analyzing experimental data, and simplifying complex mathematical models.
The versatility and simplicity of the linear interpolation formula make it a valuable tool in a wide range of applications.
Interpolation Method
There are several methods of interpolation, each suited to different scenarios and requirements. Let’s explore some of the commonly used interpolation methods:
Linear Interpolation Method
The linear interpolation method is the most basic and widely used interpolation technique. It involves connecting two known data points with a straight line and estimating the value at an intermediate point along the line. The linear interpolation formula, as discussed earlier, is used to calculate the interpolated value.
Nearest Neighbor Method
The nearest neighbor method is a simple interpolation technique that assigns the value of the nearest known data point to the interpolated point. It does not introduce any new data points but relies solely on the existing data.
Cubic Spline Interpolation Method
The cubic spline interpolation method is a more advanced technique that uses cubic polynomials to estimate values between data points. It constructs a piecewise smooth curve that passes through all the given data points.
Shape-Preservation Method
The shape-preservation method, also known as piecewise cubic Hermite interpolation (PCHIP), aims to preserve the shape and monotonicity of the data. It constructs a piecewise polynomial function that ensures the interpolated curve maintains the same trends as the original data.
Thin-plate Spline Method
The thin-plate spline method is a surface interpolation technique that uses smooth surfaces to estimate values. It is particularly useful when dealing with two-dimensional data and ensures smoothness and continuity in the interpolated surface.
Biharmonic Interpolation Method
The biharmonic interpolation method is another approach to surface interpolation. It constructs a surface by minimizing the bending energy of the thin plate spline, resulting in a smooth and continuous interpolated surface.
These are just a few of the many interpolation methods available, each suited to different types of data and requirements. The choice of interpolation method depends on the specific application and the desired properties of the interpolated values.
Solved Examples on Linear Interpolation
Let’s now explore some solved examples to illustrate the application of the linear interpolation formula and deepen our understanding of its usage.
Example 1: Finding the Interpolated Value
Suppose we have a set of values given as (2, 4) and (6, 7), and we want to find the value of y at x = 4 using linear interpolation.
Given: x = 4 x1 = 2 x2 = 6 y1 = 4 y2 = 7
Using the linear interpolation formula: y = y1 + (x – x1) * (y2 – y1) / (x2 – x1) y = 4 + (4 – 2) * (7 – 4) / (6 – 2) y = 4 + 2 * (3) / 4 y = 4 + 6 / 4 y = 4 + 1.5 y = 5.5
Therefore, the value of y at x = 4 is 5.5.
Example 2: Estimating Height
Suppose we have a table of data representing the height of a plant over time. The data is as follows:
| Day | Height (in cm) |
|---|---|
| 1 | 10 |
| 2 | 15 |
| 3 | 20 |
| 4 | ? |
We want to estimate the height of the plant on the fourth day using linear interpolation.
Given: x = 4 x1 = 3 x2 = 4 y1 = 20 y2 = ?
Using the linear interpolation formula: y = y1 + (x – x1) * (y2 – y1) / (x2 – x1) y = 20 + (4 – 3) * (y2 – 20) / (4 – 3)
To estimate the value of y2, we need more information or another data point. Let’s assume the height of the plant on the fifth day is 25 cm.
Given: x1 = 4 x2 = 5 y1 = 20 y2 = 25
Using the linear interpolation formula: y = 20 + (4 – 3) * (25 – 20) / (5 – 4) y = 20 + 5 * 5 / 1 y = 20 + 25 y = 45
Therefore, the estimated height of the plant on the fourth day is 45 cm.
Example 3: Forecasting Data
Suppose we have a set of data points given as (5, 3.5) and (10, 6), and we want to find the value of y at x = 8 using linear interpolation.
Given: x = 8 x1 = 5 x2 = 10 y1 = 3.5 y2 = 6
Using the linear interpolation formula: y = y1 + (x – x1) * (y2 – y1) / (x2 – x1) y = 3.5 + (8 – 5) * (6 – 3.5) / (10 – 5) y = 3.5 + 3 * 2.5 / 5 y = 3.5 + 7.5 / 5 y = 3.5 + 1.5 y = 5
Therefore, the value of y at x = 8 is 5.
These examples illustrate how linear interpolation can be used to estimate values between known data points and make predictions based on existing trends.
How Kunduz Can Help You Learn Linear Interpolation?
At Kunduz, we understand the importance of mastering mathematical concepts like linear interpolation. That’s why we offer a comprehensive learning platform designed to make mathematics accessible and engaging for students of all levels.
With our step-by-step lessons, interactive quizzes, and personalized feedback, you can build a solid foundation in linear interpolation and other mathematical topics. Our experienced tutors are always ready to assist you, ensuring that you receive the support you need to succeed.
Whether you’re preparing for exams, working on assignments, or simply looking to enhance your mathematical skills, Kunduz is here to help. Join us today and experience the joy of learning mathematics in a fun and effective way!
