Logarithm rules are essential tools for simplifying and manipulating logarithmic expressions. These rules establish relationships between exponential and logarithmic forms, providing a systematic approach to handle complex logarithmic computations. By applying these rules, logarithmic expressions can be expanded or condensed, making calculations more manageable and facilitating problem-solving in various mathematical and scientific applications.
What is Logarithm?
A logarithm is a mathematical function that represents the exponent to which a given number (the base) must be raised to obtain another specified number. In simpler terms, it is the power to which a base must be raised to yield a certain value. Logarithms are the inverse of exponential functions and are denoted as logb(x), where ‘b’ is the base and ‘x’ is the number. Logarithms are widely used in various fields, such as mathematics, physics, engineering, and finance, to simplify calculations involving large numbers, exponential growth, and exponential decay.
What are Log Rules?
Logarithm rules, also known as log rules or logarithmic properties, are a set of rules that govern the manipulation and simplification of logarithmic expressions. These rules are derived from the properties of exponents and provide a systematic approach to handle logarithmic computations. The key log rules include the product rule, quotient rule, power rule, zero rule, identity rule, exponential rule, change of base rule, reciprocal rule, and more. These rules allow for the transformation of complex logarithmic expressions into simpler forms, making calculations and problem-solving more efficient.
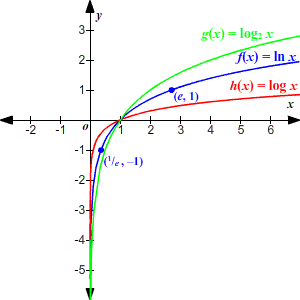
Types of Logarithm
There are two commonly used types of logarithms: common logarithm and natural logarithm.
Common logarithm
The common logarithm, denoted as log(x), is a logarithm with a base of 10. It represents the exponent to which 10 must be raised to obtain a given number ‘x’. The common logarithm is widely used in various fields, including science, engineering, and finance, to simplify calculations involving powers of 10.

Natural logarithm
The natural logarithm, denoted as ln(x), is a logarithm with a base of ‘e’, which is Euler’s number (approximately 2.71828). It represents the exponent to which ‘e’ must be raised to obtain a given number ‘x’. The natural logarithm is frequently used in mathematical and scientific applications, particularly in calculus and exponential growth/decay problems.
Logarithm Rules and Properties
Logarithm rules and properties provide a framework for manipulating and simplifying logarithmic expressions. These rules allow for the transformation of complex logarithmic expressions into simpler forms, making calculations and problem-solving more efficient. Here are some of the key logarithm rules:
Product Rule of Log
The product rule states that the logarithm of a product is equal to the sum of the logarithms of the individual factors.
Formula: logb(mn) = logb(m) + logb(n)
Example: log2(4 × 8) = log2(4) + log2(8) = 2 + 3 = 5
Quotient Rule of Log
The quotient rule states that the logarithm of a quotient is equal to the difference of the logarithms of the numerator and denominator.
Formula: logb(m/n) = logb(m) – logb(n)
Example: log3(9 / 3) = log3(9) – log3(3) = 2 – 1 = 1
Power Rule of Log
The power rule states that the logarithm of a number raised to an exponent is equal to the exponent multiplied by the logarithm of the base.
Formula: logb(mn) = n · logb(m)
Example: log5(92) = 2 · log5(9) = 2 · 0.86135 ≈ 1.7227
Zero Rule of Log
The zero rule states that the logarithm of 1 to any base is always equal to zero.
Formula: logb(1) = 0
Example: log2(1) = 0
Identity Rule of Log
The identity rule states that the logarithm of the base itself is always equal to 1.
Formula: logb(b) = 1
Example: log10(10) = 1
Exponential Rule of Log
The exponential rule states that raising the base of a logarithm to the power of the logarithm itself equals the original number.
Formula: blogb(x) = x
Example: 10log10(100) = 100
Change of Base Rule of Log
The change of base rule allows for the conversion of a logarithm with one base to a logarithm with a different base.
Formula: loga(x) = logb(x) / logb(a)
Example: log3(7) = log10(7) / log10(3)
Reciprocal Rule of Log
The reciprocal rule states that the logarithm of the reciprocal of a number is equal to the negative of the logarithm of the original number.
Formula: logb(1/x) = -logb(x)
Example: log2(1/4) = -log2(4) = -2
Base Switch Rule
The base switch rule allows for the conversion of a logarithm with one base to a logarithm with a different base.
Formula: loga(x) = logc(x) / logc(a)
Example: log3(7) = log2(7) / log2(3)
Equality of Logarithm
The equality of logarithm states that if two logarithms with the same base are equal, then their arguments are also equal.
Formula: logb(x) = logb(y) if and only if x = y
Example: log2(8) = log2(23) = 3
Number Raised to Log
The number raised to a logarithm is equal to the original number.
Formula: blogb(x) = x
Example: 10log10(100) = 100
Negative Log Rule
The negative log rule states that the logarithm of a negative number or zero is undefined. Example: log2(-1) and log2(0) are undefined
These logarithm rules and properties provide a foundation for simplifying and manipulating logarithmic expressions, allowing for more efficient calculations and problem-solving.
Logarithm Inverse Property
The logarithm inverse property states that if a number ‘x’ is equal to a logarithm with a certain base ‘b’, then the base ‘b’ raised to the power of ‘x’ is equal to the original number.
Formula: logb(bx) = x
Example: log2(23) = 3
Derivative of Log
The derivative of a logarithm function can be determined using calculus. For a natural logarithm (base ‘e’), the derivative of ln(x) is equal to 1/x. This means that the derivative of logb(x) can be calculated using the change of base formula and the derivative of the natural logarithm.
Formula: d/dx [ln(f(x))] = f'(x) / f(x)
Example: If y = ln(x2), then dy/dx = 2x / x2 = 2/x
Integration of Log
The integral of a logarithmic function can also be determined using calculus. The integral of ln(x) is equal to x · ln(x) – x + C, where C is the constant of integration. The integration of logb(x) can be calculated using the change of base formula and the integral of the natural logarithm.
Formula: ∫ln(x) dx = x · ln(x) – x + C = x · (ln(x) – 1) + C
Example: ∫ln(x2) dx = x2 · ln(x2) – x2 + C
Applications of Logarithms
Logarithms have numerous applications in mathematics, science, engineering, and finance. Some common applications of logarithms include:
- Calculation of pH levels in chemistry
- Measurement of sound intensity using the decibel scale
- Analysis of exponential growth and decay processes
- Calculation of compound interest and population growth
- Simplification of complex calculations involving large numbers
- Solving exponential equations and equations involving variable exponents
- Derivation of derivative and integral formulas in calculus
- Analysis of data and patterns in various fields, such as biology, physics, and economics

Comparison of Exponent law and Logarithm law
Exponent laws and logarithm laws are closely related and can be used interchangeably. While exponent laws deal with operations involving exponents, logarithm laws provide corresponding rules for simplifying logarithmic expressions. The relationship between exponent laws and logarithm laws can be summarized as follows:
- Product Rule: Multiplication inside the log can be turned into addition outside the log, and vice versa.
- Quotient Rule: Division inside the log can be turned into subtraction outside the log, and vice versa.
- Power Rule: An exponent on everything inside a log can be moved out front as a multiplier, and vice versa.
- Zero Rule: The logarithm of 1 to any base is always equal to zero.
- Identity Rule: The logarithm of the base itself is always equal to 1.
- Exponential Rule: Raising the base of a logarithm to the power of the logarithm itself equals the original number.
- Change of Base Rule: Allows for the conversion of a logarithm with one base to a logarithm with a different base.
- Reciprocal Rule: The logarithm of the reciprocal of a number is equal to the negative of the logarithm of the original number.
- Base Switch Rule: Allows for the conversion of a logarithm with one base to a logarithm with a different base.
- Equality of Logarithm: If two logarithms with the same base are equal, then their arguments are also equal.
- Number Raised to Log: The number raised to a logarithm is equal to the original number.
- Negative Log Rule: The logarithm of a negative number or zero is undefined.
How to Apply the Log Rules
Logarithm rules can be applied in various ways, depending on the specific problem or expression. Here are some general steps to apply the log rules:
- Identify the logarithmic expression or problem that needs to be simplified or solved.
- Determine the specific log rule that is applicable to the given situation.
- Apply the corresponding log rule to transform the expression or problem into a simpler form.
- Simplify the expression or solve the problem using basic arithmetic operations.
- Verify the solution or simplify further if necessary.
Solved Examples on Log Rules
To further illustrate the application of logarithm rules, here are some solved examples:
Example 1: Simplify the expression log2(4 × 8).
Solution: Using the product rule, we can split the product into a sum of logarithms: log2(4 × 8) = log2(4) + log2(8) = 2 + 3 = 5
Example 2: Simplify the expression log3(9 / 3).
Solution: Using the quotient rule, we can divide the quotient into a difference of logarithms: log3(9 / 3) = log3(9) – log3(3) = 2 – 1 = 1
Example 3: Simplify the expression log5(92).
Solution: Using the power rule, we can bring down the exponent as a coefficient: log5(92) = 2 · log5(9) ≈ 2 · 0.86135 ≈ 1.7227
These examples demonstrate how logarithm rules can be applied to simplify and solve logarithmic expressions.
How Kunduz Can Help You with Log Rules?
At Kunduz, we understand the importance of logarithm rules in mathematics and various scientific disciplines. Our expert team of tutors and educators is dedicated to providing comprehensive and tailored support to students in understanding and applying log rules effectively. Whether you need assistance with log simplification, logarithm equations, or logarithmic functions, Kunduz is here to help. Our experienced tutors will guide you through step-by-step explanations, offer practice problems, and ensure that you gain a solid understanding of logarithm rules. With Kunduz, you can build your confidence and excel in your mathematical endeavors.
