Logarithmic functions play a crucial role in the field of mathematics and are widely used in various scientific calculations. The term ‘logarithm‘ was first coined by John Napier, a Scottish mathematician, in the 16th century. The purpose of logarithms was to simplify mathematical calculations, especially those involving very large or very small numbers. These functions are the inverse of exponential functions, transforming multiplications into additions and divisions into subtractions.
What are Logarithmic Functions?
A logarithmic function is typically expressed as f(x) = log_b(x) (where b > 0 and b ≠ 1). Here, b represents the base of the logarithm, and x is the number for which we want to find the logarithm. In simpler terms, the logarithm of a number x to the base b is the exponent to which we need to raise b to obtain x.
For example:
If we have 2^3 = 8, then the logarithmic function would be log_2(8) = 3, which means that 2 needs to be raised to the power of 3 to get 8.
What is Logarithm?
A logarithm is, in essence, an exponent. It is a mathematical operation that determines how many times a certain number, called the base, must be multiplied by itself to obtain another number. For instance, in the expression log_3(9) = 2, the number 3 is the base, and 2 is the logarithm, meaning that 3 needs to be multiplied by itself twice to get 9.
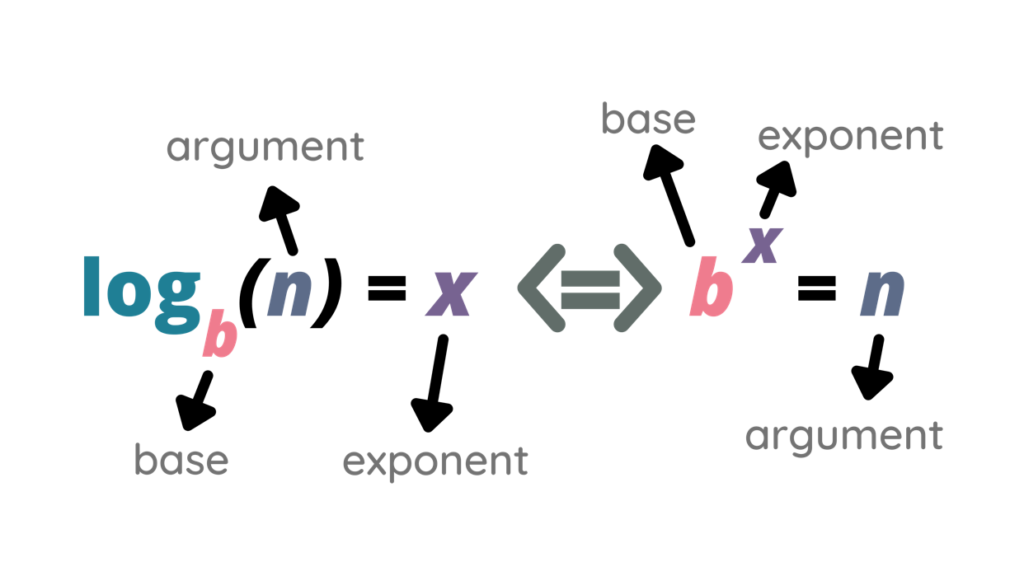
Domain and Range of Log Functions
In mathematics, the domain represents all the possible input values (usually x), and the range represents all the possible output values (usually y). For logarithmic functions, the domain includes all positive real numbers (as the logarithm of a negative number is undefined), while the range includes all real numbers.
Logarithmic Graph
The graph of a logarithmic function is a curve that starts from the positive side of the y-axis and increases or decreases, depending on the base of the logarithm. If the base is greater than 1, the graph increases, and if the base is between 0 and 1, the graph decreases. The y-axis serves as a vertical asymptote, meaning the curve gets closer to the y-axis but never actually touches or crosses it.
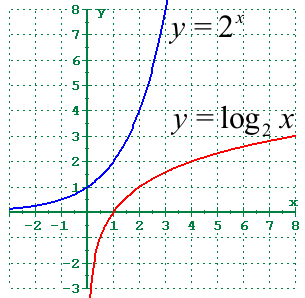
Graphing Logarithmic Functions
The process of graphing a logarithmic function involves several steps:
- Find the domain and range.
- Find the vertical asymptote by setting the argument equal to 0.
- Substitute the value of
xthat makes the argument equal to 1 and use the propertylog_b(1) = 0to find the x-intercept. - Substitute the value of
xthat makes the argument equal to the base and use the propertylog_b(b) = 1. This gives us a point on the graph. - Join the points and extend the curve on both sides with respect to the vertical asymptote.
Derivative and Integral of Logarithmic Functions
The derivative of a logarithmic function provides the slope of the tangent to the curve at a given point. The derivative of the natural logarithm ln(x) is 1/x, and the derivative of the logarithm to any other base b is 1/(x*ln(b)).
The integral of the natural logarithm ln(x) is ∫ln(x)dx = x(ln(x) - 1) + C, and the integral of the logarithm to any other base b is ∫log_b(x)dx = x(log_b(x) - 1) + C.
Properties of Logarithmic Functions
Logarithmic functions have several important properties that make working with them easier:
Product Rule
The logarithm of the product of two numbers M and N with the same base b is equal to the sum of the logarithms of the two numbers. In other words, log_b(M*N) = log_b(M) + log_b(N).
Quotient Rule
The logarithm of the quotient of two numbers M and N with the same base b is equal to the difference between the logarithms of the two numbers. This can be written as log_b(M/N) = log_b(M) - log_b(N).
Power Rule
The logarithm of a number M raised to the power p with base b is equal to the product of p and the logarithm of M. This is expressed as log_b(M^p) = p*log_b(M).
Zero Exponent Rule
The logarithm of 1 to any base is always 0. This is because any number raised to the power of 0 is 1. Therefore, log_b(1) = 0.
Change of Base Rule
The logarithm of a number N to the base a can be expressed in terms of logarithms with any other base c. The formula is log_a(N) = log_c(N)/log_c(a).
This property is particularly useful when working with logarithms of different bases.
Other Important Rules of Logarithmic Function
There are other rules as well, such as log_b(b) = 1, which signifies that the logarithm of the base to the base itself is always 1. Furthermore, log_b(b^x) = x, meaning that the logarithm of a base raised to any exponent x is always equal to x. Lastly, b^(log_b(x)) = x, which states that a base elevated to the logarithm of any number x with the same base will always be equal to x.
Types of Logarithms
There are two major types of logarithms, classified based on their base:
Common Logarithmic Function
Also known as the decadic logarithm, the common logarithmic function has a base of 10. It is usually denoted as log(x) or log_10(x).
Natural Logarithmic Function
The natural logarithmic function, often denoted as ln(x), has a base e (where e is approximately equal to 2.71828). This type of logarithm is frequently used in calculus and complex number theory due to its unique mathematical properties.
Transformations of Logarithmic Functions
Transformations of logarithmic functions refer to the changes in the graph of the function due to manipulations in the function’s equation. These transformations include vertical and horizontal shifts, stretches/compressions, and reflections.
Vertical Shifts
A vertical shift occurs when a constant is added to or subtracted from the logarithmic function. If a constant d is added to the function, the graph shifts up by d units, and if d is subtracted, the graph shifts down by d units.
Horizontal Shifts
A horizontal shift takes place when a constant is added to or subtracted from the input of the function. If a constant c is added to the input, the graph shifts left by c units, and if c is subtracted, the graph shifts right by c units.
Vertical Stretches/Compressions
A vertical stretch or compression happens when the logarithmic function is multiplied by a constant. If the function is multiplied by a constant a > 1, the graph stretches vertically by a factor of a. If 0 < a < 1, the graph is compressed vertically by a factor of a.
Horizontal Stretches/Compressions
A horizontal stretch or compression occurs when the input of the function is multiplied by a constant. If the input is multiplied by m > 1, the graph stretches horizontally by a factor of m. If 0 < m < 1, the graph is compressed horizontally by a factor of m.
Reflections
Reflections of the logarithmic function graph occur when either the function or its input is multiplied by -1. If the function is multiplied by -1, the graph reflects about the x-axis. If the input is multiplied by -1, the graph reflects about the y-axis.
Converting Between Logarithmic And Exponential Form
Logarithmic and exponential forms are closely related, as logarithmic functions are the inverse of exponential functions. The exponential form b^y = x can be converted into the logarithmic form log_b(x) = y. Similarly, the logarithmic form log_b(x) = y can be converted into the exponential form b^y = x.
Converting from Exponential to Logarithmic Form
The conversion from exponential form to logarithmic form involves identifying the base, exponent, and result in the exponential equation and rewriting them in logarithmic form. For example, the exponential equation 2^3 = 8 can be converted into logarithmic form as log_2(8) = 3.
How to Learn Logarithmic Functions?
Mastering logarithmic functions requires understanding the concepts, knowing the formulas and properties, and practicing problems regularly.
- Start by grasping the fundamental concepts of logarithms and logarithmic functions. Understand what they are, why they are used, and how they are related to exponential functions.
- Learn the formulas and properties of logarithmic functions. These include the product, quotient, and power rules, the zero exponent rule, the change of base rule, and others.
- Practice solving problems involving logarithmic functions. This can include finding the value of a logarithm, simplifying expressions using the properties of logarithms, solving equations involving logarithmic functions, and more.
- Work on graphing logarithmic functions. Understand how the graph of a logarithmic function is shaped, and how it changes due to transformations such as shifts, stretches/compressions, and reflections.
- Make use of online resources, such as educational websites and video tutorials, to learn and practice logarithmic functions. There are many free resources available that provide detailed explanations, examples, and practice problems.
Solved Examples on Logarithmic Functions
To illustrate how logarithmic functions are used in problem-solving, let’s look at a few examples:
Example 1: Simplify 2*log_2(8) + 3*log_2(4) - log_2(32).
Solution: Using the power rule of logarithms, we have log_2(8^2) + log_2(4^3) - log_2(32) = log_2(64) + log_2(64) - log_2(32) = log_2(64*64/32) = log_2(128) = 7.
Example 2: Solve the equation log_3(x) + log_3(x-2) = 2.
Solution: Using the product rule of logarithms, we can combine the two logarithms on the left side of the equation into one: log_3(x*(x-2)) = 2. This gives us log_3(x^2 - 2x) = 2. Converting to exponential form, we get 3^2 = x^2 - 2x, or x^2 - 2x - 9 = 0. Solving this quadratic equation, we find x = 3 or x = -3. However, since the domain of a logarithm is only positive real numbers, we discard x = -3 and are left with the solution x = 3.
Example 3: Graph the function f(x) = log_2(x - 1) + 3.
Solution: This function represents a logarithmic function with a horizontal shift to the right by 1 unit and a vertical shift upward by 3 units. The key points of the parent function y = log_2(x) are (1, 0), (2, 1), and (0.5, -1). Shifting these points to the right by 1 unit and upward by 3 units, we get the points (2, 3), (3, 4), and (1.5, 2). These points, along with the vertical asymptote x = 1, allow us to sketch the graph of the function.
How Kunduz Can Help You Learn Logarithmic Functions?
Kunduz is an educational platform that provides a wealth of resources for learning mathematics, including logarithmic functions. It offers personalized learning experiences, with access to a vast database of step-by-step solutions, video lessons, practice problems, and more. With Kunduz, you can learn at your own pace, get instant help when you need it, and monitor your progress to ensure that you are on track towards mastering logarithmic functions and other mathematical concepts. As a trusted companion in your learning journey, Kunduz empowers you to achieve your academic goals with convenience, efficiency, and affordability.
