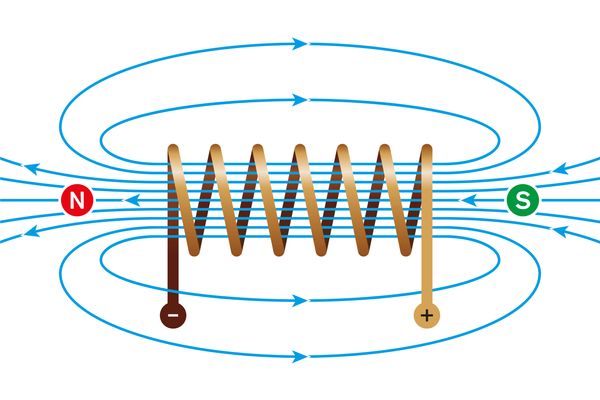
Magnetic flux, a cornerstone in the study of electromagnetism, is a fundamental concept that has a profound impact on our daily lives. It’s instrumental in the functioning of many everyday devices, from electric motors to transformers, and even the data storage on our computers. The concept of magnetic flux is somewhat abstract, but it is crucial in understanding the working principles of many electrical and electronic devices.
What is Magnetic Flux?
Magnetic flux, represented by the Greek letter Phi (Φ or ΦB), is a measure of the total magnetic field passing through a given surface. It essentially quantifies the number of magnetic field lines that intersect a given area. The surface in question could be of any size and orientation relative to the direction of the magnetic field.

Magnetic Flux Symbol
Magnetic flux is typically denoted using the Greek letter Phi or Phi with a suffix B (ΦB). The usage of this symbol emphasizes the association of the magnetic flux with the magnetic field (B).
Magnetic Flux Formula
The formula for magnetic flux is a scalar product of the magnetic field (B) and the area (A) through which it passes. The scalar product takes into account not just the magnitude of the field and area, but also the angle between them. The formula for magnetic flux (ΦB) is given by:
ΦB = B.A = BA cos θ
Where:
- ΦB is the magnetic flux,
- B is the magnetic field (measured in tesla in the SI system),
- A is the area through which the field lines pass (measured in square meters in the SI system),
- θ is the angle between the magnetic field vector and the normal (perpendicular) to the area.
Magnetic Flux Equation
The magnetic flux equation, as stated above, is a scalar product of the magnetic field and the area vector. However, if the magnetic field is non-uniform, meaning it differs in magnitude and direction at different parts of the surface, the total magnetic flux through the surface is given by the sum of the product of the magnetic field and the infinitesimal area elements. Mathematically, it can be represented as:
ΦB = ∑ Bi . dAi
Magnetic Flux Unit
The measurement of magnetic flux is typically done using a device known as a flux meter. The SI unit of magnetic flux is the Weber (Wb), named after the German physicist Wilhelm Weber. A Weber can be defined as the magnetic flux that, linking a circuit of one turn, would produce in it an electromotive force of 1 volt if it were reduced to zero at a uniform rate in 1 second. The CGS unit for magnetic flux is the Maxwell (Mx).
Measurement of Magnetic Flux
The SI unit of magnetic flux is Weber (Wb) or volt-seconds, while the CGS unit is Maxwell. In practical measurements, a flux meter is often used. This device measures the change in magnetic flux by sensing the voltage induced in a coil. The reading of the flux meter is in Weber (in the SI system) or in Maxwell (in the CGS system).
Magnetic Flux Density
Magnetic flux density, represented by the symbol B, is defined as the amount of force acting per unit current per unit length on a wire placed at right angles to the magnetic field. It is a measure of the strength of the magnetic field at a particular point and is measured in Tesla (T) in the SI system or Gauss (G) in the CGS system.
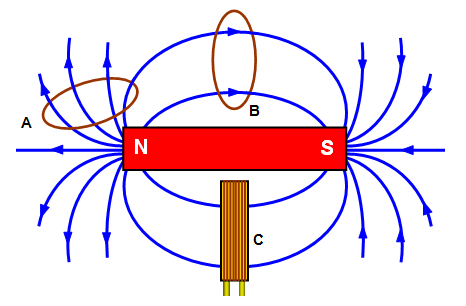
Magnetic Flux Density Formula
The formula for magnetic flux density (B) is represented as:
B = F / (I*l)
Where:
- F is the total force acting on the wire,
- I is the current flowing through the wire, and
- l is the length of the wire.
Properties of Magnetic Flux
- Magnetic flux always forms a closed loop, originating from the north pole and ending at the south pole of a magnet.
- Magnetic flux is a scalar quantity, meaning it only has magnitude and no direction.
- The magnetic flux through a given area depends not only on the magnitude of the field but also on the angle between the field lines and the normal to the area.
Conditions for Maximum and Minimum Magnetic Flux
The angle at which the magnetic field lines intersect the surface area plays a significant role in determining the magnetic flux. If the field lines intersect the area at a glancing angle (θ = 90°), the resulting flux is very low or even zero. On the other hand, if the field lines are perpendicular to the surface (θ = 0°), the resulting flux is maximum.
Difference between Magnetic Field and Magnetic Flux
While both magnetic field and magnetic flux are crucial concepts in electromagnetism, they are not the same. The magnetic field, denoted by B, is a vector quantity that quantifies the strength and direction of the magnetic force at a point in space. On the other hand, magnetic flux, denoted by ΦB, is a scalar quantity that measures the total magnetic field passing through a given surface area.
| Magnetic Field | Magnetic Flux |
|---|---|
| Vector quantity | Scalar quantity |
| Denoted by B | Denoted by ΦB |
| SI unit is Tesla (T) | SI unit is Weber (Wb) |
| Describes the strength and direction of the magnetic force at a point in space | Measures the total magnetic field passing through a given surface area |
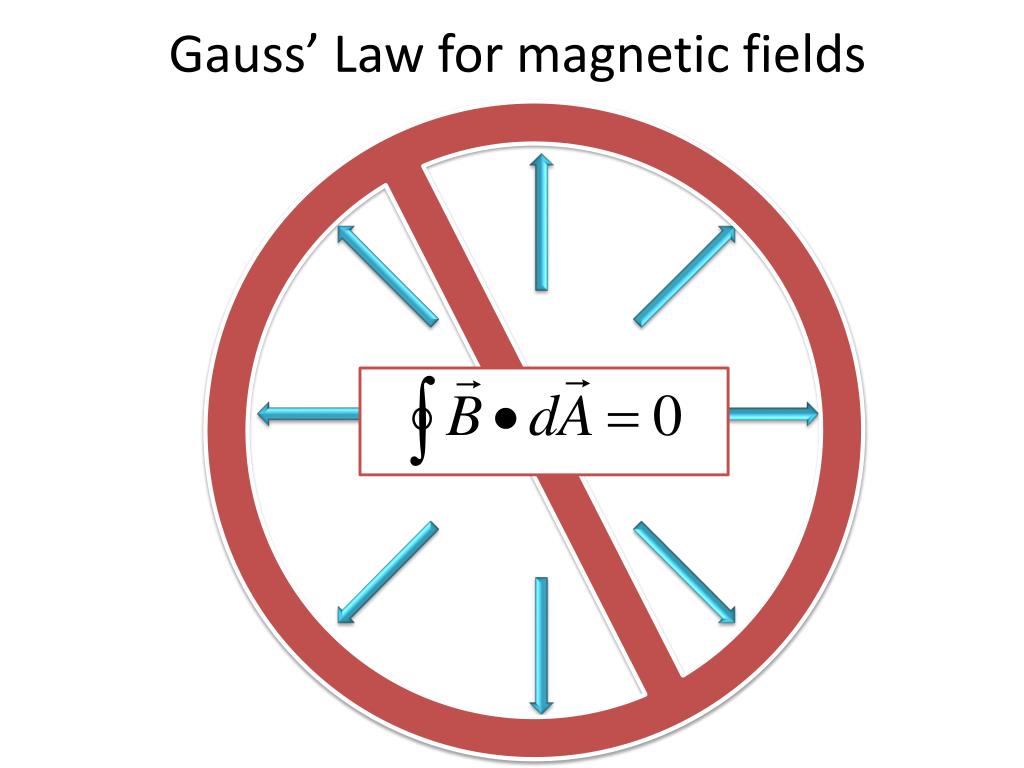
Gauss Law of Magnetism
Gauss’s law for magnetism states that the net magnetic flux passing through any closed surface in a magnetic field is zero. This is because magnetic field lines form closed loops, and for every field line that enters a closed surface, there is an equal and corresponding field line that exits the surface.
Change in Magnetic Flux
Any change in magnetic flux through a closed loop of wire induces an electromotive force (EMF) in the wire, a phenomenon known as electromagnetic induction. The magnitude of the induced EMF is directly proportional to the rate of change of magnetic flux, as given by Faraday’s law of electromagnetic induction.
Faraday’s Law of Induction and Lenz’s Law
Faraday’s law of electromagnetic induction states that the induced electromotive force (EMF) in a closed circuit is directly proportional to the time rate of change of magnetic flux through the circuit. On the other hand, Lenz’s law gives the direction of the induced EMF and current resulting from electromagnetic induction. It states that the induced EMF and the change in flux have opposite signs, which indicates that the induced EMF always works to oppose the change in magnetic flux that produced it.
Right Hand Rule Magnetic Flux
The right-hand rule is a simple way to remember the direction of magnetic field lines and the orientation of the force on a charge moving in a magnetic field. According to the right-hand rule, if you point your thumb in the direction of the current in a wire, and let your fingers curl naturally, your fingers will point in the direction of the magnetic field lines.

Solved Examples on Magnetic Flux
To further your understanding of magnetic flux, here are a few solved examples.
Example 1: A circular loop of radius 0.3 m is placed in a uniform magnetic field of 0.8 T such that the plane of the loop makes an angle of 60° with the magnetic field. Find the magnetic flux through the loop.
Solution: Given, B = 0.8 T, A = π(0.3)^2 m², θ = 60°. Using the formula ΦB = BA cos θ, we get ΦB = 0.8 * π(0.3)^2 * cos 60° = 0.113 Tm² or Wb.
Example 2: A square loop of side 0.1 m is placed in a magnetic field of 0.5 T. What is the magnetic flux through the loop if the plane of the loop is parallel to the magnetic field?
Solution: Given, B = 0.5 T, A = (0.1)^2 m², θ = 0° (since the loop is parallel to the field). Using the formula ΦB = BA cos θ, we get ΦB = 0.5 * (0.1)^2 * cos 0° = 0.005 Tm² or Wb.
How Kunduz Can Help You Learn Magnetic Flux?
Kunduz, an educational platform, provides an interactive and engaging learning experience for students. With a wide range of detailed solutions, Kunduz can help you master the concept of magnetic flux. With Kunduz, learning becomes fun and fruitful, ensuring you are ready to tackle any question related to magnetic flux.
Related Topics:
AC vs. DC: Difference Between Alternative Current (AC) and Direct Current
Ohm’s Law: Statement, Formula, Solved Examples, Verification, FAQs