Matrix multiplication is a fundamental operation in linear algebra, playing a crucial role in various mathematical and scientific fields. It allows us to combine and manipulate matrices to solve complex problems and model real-world scenarios. Understanding matrix multiplication is essential for anyone studying mathematics, physics, computer science, or engineering.
In this article, we will explore the concept of matrix multiplication, its rules, properties, and applications. We will delve into the step-by-step process of multiplying matrices and provide examples to illustrate the concepts. By the end of this article, you will have a solid understanding of matrix multiplication and its significance in various disciplines.
What is Matrix Multiplication?
Matrix multiplication is a binary operation that combines two matrices to produce a new matrix. It involves multiplying the corresponding elements of rows and columns in the matrices and summing the results. The resulting matrix has a number of rows equal to the number of rows in the first matrix and a number of columns equal to the number of columns in the second matrix.
To perform matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. This condition ensures that the matrices are compatible for multiplication. The product of two matrices, A and B, is denoted as AB.
Matrix multiplication is not commutative, which means that the order of multiplication matters. In general, AB does not equal BA. It is important to note that not all pairs of matrices can be multiplied together. The dimensions of the matrices must satisfy the compatibility condition mentioned earlier.

Matrix multiplication by Scalar
Before diving into the process of multiplying two matrices, let’s start with a simpler operation: scalar multiplication. Scalar multiplication involves multiplying a matrix by a scalar, which is a single number. In this case, every element in the matrix is multiplied by the scalar value.
For example, if we have a matrix A and a scalar k, the scalar multiplication is denoted as kA. Each element in the resulting matrix kA is obtained by multiplying the corresponding element in matrix A by the scalar value k.
Matrix Multiplication Condition
Matrix multiplication is only possible when the number of columns in the first matrix is equal to the number of rows in the second matrix. This condition ensures that the matrices are compatible for multiplication.
In general, if matrix A has dimensions m×n and matrix B has dimensions n×p, then the resulting product matrix AB will have dimensions m×p. The number of columns in matrix A must be equal to the number of rows in matrix B for matrix multiplication to be defined.
How to Multiply Matrices?
Matrix multiplication can be performed using a step-by-step process. The first step involves checking the compatibility of the matrices. If the number of columns in the first matrix equals the number of rows in the second matrix, the matrices are compatible for multiplication.
The subsequent step involves multiplying the elements in the first row of the first matrix with the elements in the first column of the second matrix and summing the products. This process is repeated for each row of the first matrix and each column of the second matrix. The final step involves placing the calculated values in their respective positions in the resultant matrix.
Notation
In matrix multiplication, we represent the product of two matrices A and B as AB. The order of the product matrix is determined by the dimensions of the original matrices. If matrix A has dimensions m×n and matrix B has dimensions n×p, the resulting product matrix AB will have dimensions m×p.
It is important to note that the order of multiplication matters. AB does not equal BA in general, unless special conditions are met.
Matrix Multiplication Formula
The formula for matrix multiplication involves the dot product of the rows of the first matrix with the columns of the second matrix. If A and B are the given matrices, then the product matrix C is defined as follows: Cxy = Ax1By1 + Ax2By2 + … + AxnByn. This formula is applicable for matrices of any order.
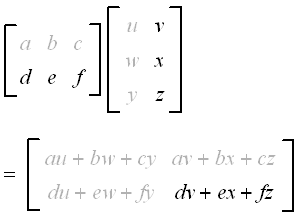
Algorithm for Matrix Multiplication
There are various algorithms for performing matrix multiplication efficiently. These algorithms aim to minimize the computational complexity of the multiplication process. Some of the commonly used algorithms are:
- Iterative Algorithm: This algorithm involves iterating over the rows and columns of the matrices to calculate the resulting matrix element by element.
- Divide and Conquer Algorithm: This algorithm divides the matrices into smaller submatrices and recursively calculates the product of these submatrices.
- Strassen’s Algorithm: Strassen’s algorithm is a recursive algorithm that reduces the number of multiplications required for matrix multiplication, leading to faster computation.
- These algorithms distribute the matrix multiplication task across multiple processors or machines to achieve parallel processing and speed up the computation.
These algorithms are widely used in various programming languages, such as C and Java, to perform efficient matrix multiplication.
2×2 Matrix Multiplication
Let’s consider a simple 2×2 matrix multiplication to understand the process. Suppose we have matrix A:
A = [[a, b], [c, d]]
And matrix B:
B = [[e, f], [g, h]]
To multiply these matrices, we follow the matrix multiplication formula:
AB = [[ae + bg, af + bh], [ce + dg, cf + dh]]
So, the resulting matrix AB is:
AB = [[ae + bg, af + bh], [ce + dg, cf + dh]]
This formula calculates the product of two 2×2 matrices by multiplying the corresponding elements and summing the results.
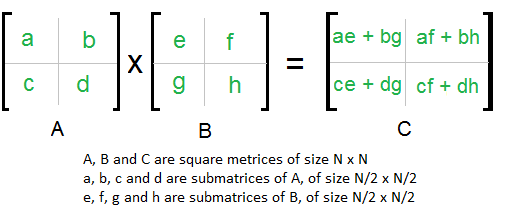
3×3 Matrix Multiplication
The process of matrix multiplication is similar for matrices of any order. Let’s consider a 3×3 matrix multiplication to illustrate. Suppose we have matrix P:
P = [[p1, p2, p3], [p4, p5, p6], [p7, p8, p9]]
And matrix Q:
Q = [[q1, q2, q3], [q4, q5, q6], [q7, q8, q9]]
To multiply these matrices, we use the matrix multiplication formula:
AB = [[p1q1 + p2q4 + p3q7, p1q2 + p2q5 + p3q8, p1q3 + p2q6 + p3q9], [p4q1 + p5q4 + p6q7, p4q2 + p5q5 + p6q8, p4q3 + p5q6 + p6q9], [p7q1 + p8q4 + p9q7, p7q2 + p8q5 + p9q8, p7q3 + p8q6 + p9q9]]
So, the resulting matrix AB is:
AB = [[p1q1 + p2q4 + p3q7, p1q2 + p2q5 + p3q8, p1q3 + p2q6 + p3q9], [p4q1 + p5q4 + p6q7, p4q2 + p5q5 + p6q8, p4q3 + p5q6 + p6q9], [p7q1 + p8q4 + p9q7, p7q2 + p8q5 + p9q8, p7q3 + p8q6 + p9q9]]
This formula calculates the product of two 3×3 matrices by multiplying the corresponding elements and summing the results.
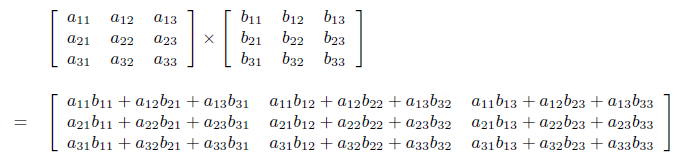
Properties of Matrix Multiplication
Matrix multiplication possesses several properties that define its behavior and enable efficient computations. Let’s explore some of these properties:
- Non-Commutative Property: Matrix multiplication is generally not commutative. In other words, AB does not equal BA, unless special conditions are met.
- Associative Property: Matrix multiplication is associative. For matrices A, B, and C that can be multiplied, (AB)C = A(BC). The grouping of matrices does not affect the result.
- Distributive Property: Matrix multiplication distributes over matrix addition. For matrices A, B, and C, A(B + C) = AB + AC. The multiplication distributes over the sum of matrices.
- Multiplicative Identity Property: The identity matrix serves as the multiplicative identity for matrix multiplication. For any matrix A, AI = IA = A, where I is the identity matrix.
- Transpose Property: The transpose of a matrix product is equal to the product of the transposes of the individual matrices. In other words, (AB)T = BTAT.
- Dimension Property: The dimensions of the resulting matrix for matrix multiplication are determined by the dimensions of the original matrices. If matrix A has dimensions m×n and matrix B has dimensions n×p, then the resulting matrix AB will have dimensions m×p.
- Determinant Property: The determinant of the product of two matrices is equal to the product of the determinants of the individual matrices. In mathematical terms, det(AB) = det(A) × det(B).
- Multiplicative Property of Zero: If any one of the matrices being multiplied is a zero matrix, the resulting product will also be a zero matrix.
These properties help in simplifying calculations and understanding the behavior of matrix multiplication.
Frequently Asked Questions About Matrix Multiplication
How to multiply two given matrices?
Matrix multiplication involves multiplying the corresponding elements of the rows and columns in two matrices and summing the results. Ensure that the number of columns in the first matrix is equal to the number of rows in the second matrix for multiplication to be possible.
What is Matrix Multiplication in Linear Algebra?
Matrix multiplication is a binary operation that combines two matrices to produce a new matrix. It is a fundamental operation in linear algebra, allowing us to solve systems of equations, represent linear transformations, and perform various calculations.
When is Matrix Multiplication Possible?
Matrix multiplication is possible when the number of columns in the first matrix is equal to the number of rows in the second matrix. This condition ensures that the matrices are compatible for multiplication.
Is Matrix Multiplication Always Commutative?
No, matrix multiplication is generally not commutative. In other words, AB does not equal BA in general, unless special conditions are met.
Is Matrix Multiplication Always Defined?
No, matrix multiplication is not always defined. It is only possible when the number of columns in the first matrix is equal to the number of rows in the second matrix.
Is Matrix Multiplication Associative?
Yes, matrix multiplication is associative. For matrices A, B, and C that can be multiplied, (AB)C = A(BC). The grouping of matrices does not affect the result.
These frequently asked questions provide insights into common queries about matrix multiplication and help clarify any confusions.
Solved Examples on Matrix Multiplication
Let’s explore some solved examples to further solidify our understanding of matrix multiplication.
Example 1: Multiply the matrices A and B:
A = [[2, 3], [4, 1]] B = [[5, 2], [6, 3]]
Solution: To multiply these matrices, we follow the matrix multiplication formula:
AB = [[(2 * 5) + (3 * 6), (2 * 2) + (3 * 3)], [(4 * 5) + (1 * 6), (4 * 2) + (1 * 3)]]
Simplifying the calculations:
AB = [[10 + 18, 4 + 9], [20 + 6, 8 + 3]] = [[28, 13], [26, 11]]
Therefore, the resulting matrix AB is:
AB = [[28, 13], [26, 11]]
Example 2: Multiply the matrices C and D:
C = [[1, 2, 3], [4, 5, 6]] D = [[7], [8], [9]]
Solution: To multiply these matrices, we follow the matrix multiplication formula:
CD = [[(1 * 7) + (2 * 8) + (3 * 9)], [(4 * 7) + (5 * 8) + (6 * 9)]]
Simplifying the calculations:
CD = [[7 + 16 + 27], [28 + 40 + 54]] = [[50], [122]]
Therefore, the resulting matrix CD is:
CD = [[50], [122]]
These solved examples demonstrate the step-by-step process of multiplying matrices and obtaining the resulting matrix.
How Kunduz Can Help You Learn Matrix Multiplication?
At Kunduz, we understand the importance of mastering matrix multiplication in various academic and professional fields. We offer comprehensive resources, tutorials, and exercises to help you learn and understand matrix multiplication effectively.
Our website provides interactive tools and calculators to perform matrix multiplication, making the learning process engaging and practical. With step-by-step instructions and examples, you can gain a solid understanding of the concepts and apply them to solve real-world problems.
Whether you are a student, professional, or enthusiast, Kunduz is here to support your learning journey. Visit our website today to explore our resources and enhance your understanding of matrix multiplication.
In conclusion, matrix multiplication is a fundamental operation in linear algebra, allowing us to combine and manipulate matrices to solve complex problems. By following the rules and properties of matrix multiplication, we can perform calculations efficiently and obtain accurate results. Understanding matrix multiplication is essential for various fields, and with Kunduz’s resources, you can master this concept and excel in your academic and professional pursuits.
