In the field of statistics, mean, median, and mode are measures of central tendency that help summarize and analyze data sets. These measures provide valuable insights into the “typical” or representative value of a data set, allowing researchers and analysts to gain a deeper understanding of the data.
Mean is the most commonly used measure of central tendency. It represents the average value of a data set and is calculated by adding up all the values and dividing by the total number of values. The mean is denoted by the symbol x̅ or μ.
Median is the middle value of a data set when the values are arranged in ascending or descending order. If there is an odd number of values, the median is the middle value. If there is an even number of values, the median is the average of the two middle values.
Mode is the value that appears most frequently in a data set. It is the value with the highest frequency. A data set can have one mode (unimodal), two modes (bimodal), or more than two modes (multimodal). If all values occur with the same frequency, there is no mode.
These measures of central tendency play a crucial role in various fields, including mathematics, science, economics, and social sciences. They provide a basis for analyzing and interpreting data, making predictions, and drawing conclusions.
Measures of Central Tendency
Measures of central tendency are statistical values that represent the center of a data set. They summarize the data and provide information about the “typical” value. The three main measures of central tendency are mean, median, and mode.
- Mean: The mean is the average value of a data set. It is calculated by adding up all the values and dividing by the total number of values. The mean is affected by extreme values, so it may not always be a good representation of the data set.
- Median: The median is the middle value of a data set. It is the value that separates the higher half from the lower half when the data is arranged in order. The median is not affected by extreme values and is often used when there are outliers in the data.
- Mode: The mode is the value that appears most frequently in a data set. It represents the peak or the most common value in the data. A data set can have multiple modes or no mode at all.
These measures provide different perspectives on the data and can be used together to gain a comprehensive understanding of the data set.

What is Mean?
Mean is the most commonly used measure of central tendency. It represents the average value of a data set. The mean is calculated by adding up all the values in the data set and dividing by the total number of values.
The formula to calculate the mean is:
Mean (x̅) = Sum of Values / Number of Values
For example, let’s consider a data set of test scores: 80, 90, 70, 85, 95. To find the mean, we add up all the values (80 + 90 + 70 + 85 + 95 = 420) and divide by the total number of values (5). Therefore, the mean is 420 / 5 = 84.
The mean is widely used in various fields, such as calculating average grades, determining the average temperature, or finding the average sales for a company. It provides a general representation of the data and is often used as a benchmark for comparison.
What is Median?
Median is the middle value of a data set. It is the value that separates the higher half from the lower half when the data is arranged in order. The median is not affected by extreme values and is a robust measure of central tendency.
To find the median, the data set must be arranged in ascending or descending order. If there is an odd number of values, the median is the middle value. If there is an even number of values, the median is the average of the two middle values.
For example, let’s consider a data set of test scores: 80, 90, 70, 85, 95. When arranged in ascending order, the data set becomes: 70, 80, 85, 90, 95. Since there are five values, the median is the middle value, which is 85.
The median is often used when there are outliers in the data or when the data is not normally distributed. It provides a measure of central tendency that is less influenced by extreme values.
What is Mode?
Mode is the value that appears most frequently in a data set. It represents the peak or the most common value in the data. A data set can have one mode (unimodal), two modes (bimodal), or more than two modes (multimodal). If all values occur with the same frequency, there is no mode.
For example, let’s consider a data set of test scores: 80, 90, 70, 85, 95. In this data set, the mode is the value that appears most frequently. Since all values occur only once, there is no mode in this data set.
In another example, let’s consider a data set of test scores: 80, 90, 70, 85, 95, 90. In this data set, the mode is 90 because it appears twice, which is more than any other value.
The mode is useful when there are repeated values in the data set. It provides insight into the most common value or values in the data.
What is Range?
Range is the difference between the highest value and the lowest value in a data set. It provides a measure of the spread or variability of the data. The range is calculated by subtracting the lowest value from the highest value.
For example, let’s consider a data set of test scores: 80, 90, 70, 85, 95. The highest value is 95 and the lowest value is 70. Therefore, the range is 95 – 70 = 25.
The range is a simple measure of dispersion that gives an idea of how spread out the values are in the data set. However, it does not provide information about the distribution of the data between the highest and lowest values.
How To Find/Calculate Mean?
To calculate the mean of a data set, follow these steps:
Step 1: Add up all the values in the data set.
Step 2: Divide the sum by the total number of values.
Let’s use an example to illustrate how to calculate the mean. Consider the following data set: 10, 20, 30, 40, 50.
Step 1: Add up all the values: 10 + 20 + 30 + 40 + 50 = 150.
Step 2: Divide the sum by the total number of values: 150 / 5 = 30.
Therefore, the mean of the data set is 30.
It is important to note that the mean is influenced by extreme values, so it may not always be a good representation of the data set. In such cases, the median or mode may provide a more accurate measure of central tendency.
Mean Formula
The mean of a data set can be calculated using the following formula:
Mean (x̅) = Sum of Values / Number of Values
In this formula, the sum of values is obtained by adding up all the values in the data set, and the number of values represents the total count of values.
For example, let’s consider a data set of test scores: 80, 90, 70, 85, 95. To find the mean, we add up all the values (80 + 90 + 70 + 85 + 95 = 420) and divide by the total number of values (5). Therefore, the mean is 420 / 5 = 84.
The mean formula is a straightforward way to calculate the average value of a data set and is widely used in various fields.
Mean of Grouped Data
In some cases, the data set may be grouped into intervals or classes. To calculate the mean of grouped data, different methods can be used depending on the available information.
The three common methods for calculating the mean of grouped data are:
- Direct Method: In this method, the mean is calculated by multiplying each value by its corresponding frequency, adding up these products, and dividing by the total frequency.
- Assumed Mean Method: This method involves assuming a value for the mean and then adjusting the calculations based on the deviations from this assumed mean.
- Step Deviation Method: This method is similar to the assumed mean method but involves using step deviations instead of raw deviations. Step deviations are obtained by subtracting the assumed mean from each value and dividing by a common step value.
To calculate the mean of grouped data using these methods, specific formulas and calculations are used. The appropriate method depends on the available information and the specific requirements of the analysis.
How To Find/Calculate Median?
To find the median of a data set, follow these steps:
Step 1: Arrange the data set in ascending or descending order.
Step 2: Determine if the number of values is odd or even.
- If the number of values is odd, the median is the middle value of the data set.
- If the number of values is even, the median is the average of the two middle values.
Let’s use an example to illustrate how to calculate the median. Consider the following data set: 10, 20, 30, 40, 50.
Step 1: Arrange the data set in ascending order: 10, 20, 30, 40, 50.
Step 2: Since there are five values, which is an odd number, the median is the middle value. In this case, the middle value is 30.
Therefore, the median of the data set is 30.
The median provides a measure of central tendency that is not affected by extreme values. It is often used when there are outliers in the data or when the data is not normally distributed.
Median Formula
The formula to calculate the median depends on whether the number of values in the data set is odd or even.
If the number of values (n value) in the data set is odd, the formula to calculate the median is:
Median = [(n + 1)/2]th term
If the number of values (n value) in the data set is even, the formula to calculate the median is:
Median = [(n/2)th term + {(n/2) + 1}th term] / 2
In these formulas, the term represents the position of the middle value(s) in the data set.
For example, let’s consider a data set of test scores: 80, 90, 70, 85, 95. When arranged in ascending order, the data set becomes: 70, 80, 85, 90, 95. Since there are five values, the median is the middle value, which is 85.
The median formula allows for the calculation of the middle value(s) in a data set, providing a measure of central tendency that is not affected by extreme values.
Median of Grouped Data
Similar to the mean, the median can also be calculated for grouped data. However, the approach is slightly different, and specific formulas are used.
To calculate the median of grouped data, the following formula is used:
Median = l + [(n/2 – cf) / f]×h
In this formula, l represents the lower limit of the median class, n represents the total number of observations, cf represents the cumulative frequency of the class preceding the median class, f represents the frequency of the median class, and h represents the size of the class interval.
The median of grouped data provides a measure of central tendency that takes into account the intervals or classes in which the data is grouped. It allows for the analysis and interpretation of data sets that are not presented as individual values.
How To Find/Calculate Mode?
To find the mode of a data set, follow these steps:
Step 1: Identify the value(s) that appear most frequently in the data set.
Step 2: If there is one value with the highest frequency, it is the mode. If there are multiple values with the same highest frequency, the data set is multimodal.
Let’s use an example to illustrate how to calculate the mode. Consider the following data set: 10, 20, 30, 20, 40, 30, 50.
Step 1: Identify the values that appear most frequently. In this data set, the values 20 and 30 both appear twice, which is the highest frequency.
Step 2: Since there are multiple values with the same highest frequency, the data set is multimodal. The mode is 20 and 30.
The mode provides insight into the most common value(s) in a data set. It is useful when there are repeated values and allows for a better understanding of the distribution of the data.
Mode Formula
The mode of a data set is the value that appears most frequently. It can be calculated using the following formula for grouped data:
Mode = l + [(f1 – f0) / (2f1 – f0 – f2)] × h
In this formula, l represents the lower limit of the modal class, f1 represents the frequency of the modal class, f0 represents the frequency of the class preceding the modal class, f2 represents the frequency of the class succeeding the modal class, and h represents the size of the class interval.
The mode formula allows for the calculation of the most frequently occurring value(s) in a data set, providing insights into the distribution and patterns of the data.
Mode of Grouped Data
Similar to the mean and median, the mode can also be calculated for grouped data. The approach and formula for calculating the mode of grouped data are different from those for individual values.
To calculate the mode of grouped data, the following formula is used:
Mode = l + [(f1 + f0) / (2f1 – f0 – f2)] × h
In this formula, l represents the lower limit of the modal class, f1 represents the frequency of the modal class, f0 represents the frequency of the class preceding the modal class, f2 represents the frequency of the class succeeding the modal class, and h represents the size of the class interval.
The mode of grouped data allows for the analysis and interpretation of data sets that are presented in intervals or classes, providing insights into the most frequently occurring value(s) within those intervals.
How To Find/Calculate Range?
To calculate the range of a data set, follow these steps:
Step 1: Identify the highest value and the lowest value in the data set.
Step 2: Subtract the lowest value from the highest value to obtain the range.
Let’s use an example to illustrate how to calculate the range. Consider the following data set: 10, 20, 30, 40, 50.
Step 1: Identify the highest value, which is 50, and the lowest value, which is 10.
Step 2: Subtract the lowest value from the highest value: 50 – 10 = 40.
Therefore, the range of the data set is 40.
The range provides a measure of the spread or variability of the data. It gives an idea of how the values are distributed between the highest and lowest values in the data set.
Range Formula
The range of a data set is calculated by subtracting the lowest value from the highest value:
Range = Highest Value – Lowest Value
In this formula, the highest value represents the largest value in the data set, and the lowest value represents the smallest value in the data set.
For example, let’s consider a data set of test scores: 80, 90, 70, 85, 95. The highest value is 95 and the lowest value is 70. Therefore, the range is 95 – 70 = 25.
The range formula is a simple way to calculate the spread or variability of the data, providing insights into how the values are distributed.
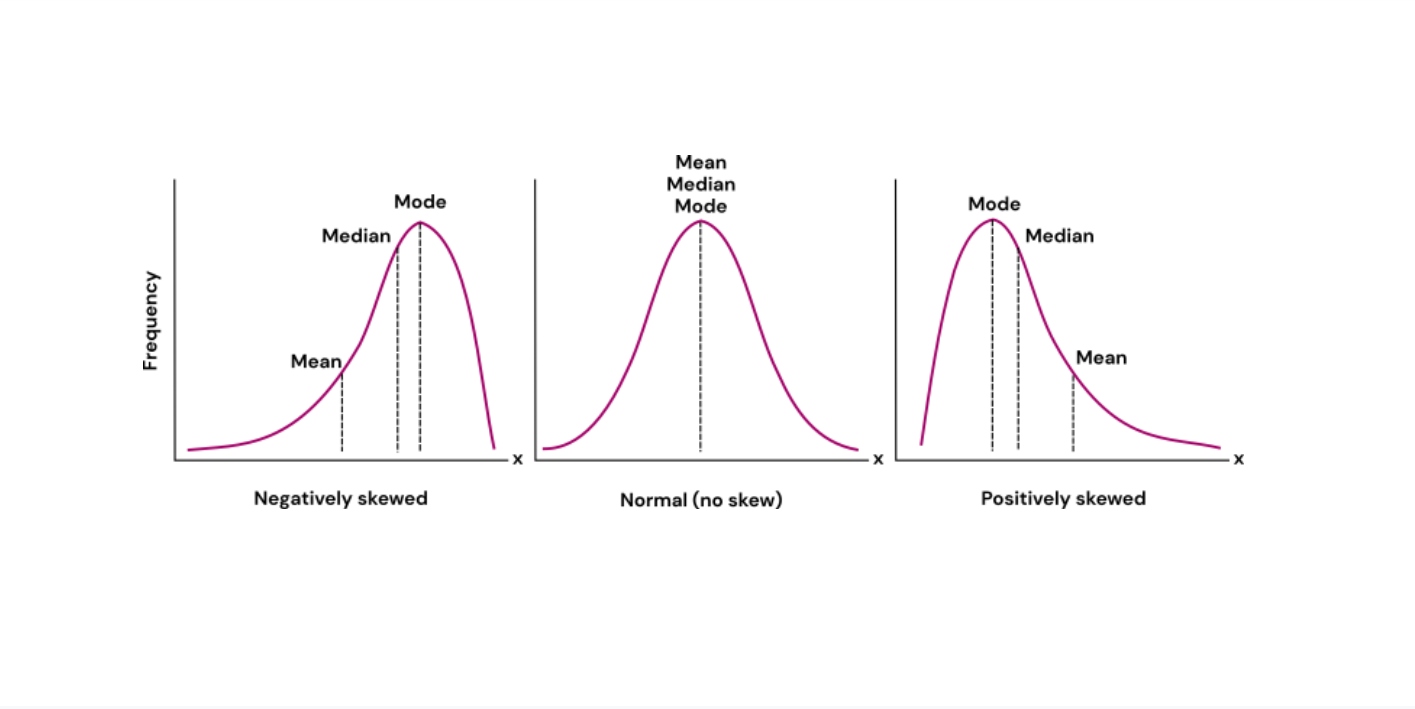
Relation Between Mean Median Mode
Mean, median, and mode are all measures of central tendency that provide different perspectives on a data set. While they represent different aspects of the data, there is a relationship between these measures.
For a unimodal, symmetric data set, the mean, median, and mode are approximately equal. In this case, the data is evenly distributed around the central value, resulting in similar values for the mean, median, and mode.
However, for a skewed or multimodal data set, the mean, median, and mode may differ. In a positively skewed data set, where the tail is on the right side, the mean is usually greater than the median, which is greater than the mode. In a negatively skewed data set, where the tail is on the left side, the mean is usually less than the median, which is less than the mode.
The relationship between mean, median, and mode can provide insights into the shape and distribution of the data. It helps researchers and analysts understand the characteristics of the data set and make informed decisions based on the central tendency measures.

Mean, Median, Mode (Table)
To summarize the concepts of mean, median, and mode, let’s refer to the following table:
| Measure of Central Tendency | Definition | Calculation |
|---|---|---|
| Mean | The average value of a data set | Sum of values / Number of values |
| Median | The middle value of a data set | Middle value when arranged in order |
| Mode | The most frequently occurring value in a data set | Value with the highest frequency |
The table provides a quick reference for understanding the definitions and calculations of mean, median, and mode. These measures of central tendency are fundamental tools in statistical analysis and play a crucial role in summarizing and interpreting data sets.
Mean Median Mode Formula
The relationship between mean, median, and mode can be expressed using the following formula:
Mode = 3 Median – 2 Mean
This formula highlights the relationship between the three measures of central tendency. The mode is approximately three times the median minus two times the mean.
While this formula provides a general relationship between the measures, it may not hold true for all data sets, especially when there are extreme values or outliers. It is important to consider the characteristics of the data set and interpret the measures of central tendency accordingly.
Difference Between Mean, Median, and Mode
Mean, median, and mode are measures of central tendency that provide different insights into a data set. Here are the key differences between these measures:
- Mean: The mean represents the average value of a data set. It is calculated by summing up all the values and dividing by the total number of values. The mean is influenced by extreme values and provides a measure of the overall “typical” value.
- Median: The median is the middle value of a data set. It is the value that separates the higher half from the lower half when the data is arranged in order. The median is not affected by extreme values and provides a measure of the central value.
- Mode: The mode is the value that appears most frequently in a data set. It represents the peak or the most common value in the data. A data set can have multiple modes or no mode at all.
The choice of measure depends on the characteristics of the data set and the specific requirements of the analysis. The mean is commonly used when there are no extreme values or outliers. The median is preferred when there are outliers or the data is not normally distributed. The mode is useful when there are repeated values.
Understanding the differences between mean, median, and mode allows researchers and analysts to choose the appropriate measure for their data analysis and interpretation.
Frequently Asked Questions About Mean, Median, and Mode
Q: What do mean, median, and mode represent?
A: Mean, median, and mode are measures of central tendency that represent the “typical” or representative value of a data set. They provide insights into the central value, the most common value, and the average value, respectively.
Q: Which measure of central tendency is influenced by extreme values?
A: The mean is influenced by extreme values because it takes into account all the values in the data set. A single extreme value can significantly impact the mean.
Q: When should I use the median instead of the mean?
A: The median is preferred when there are outliers or the data is not normally distributed. It provides a measure of central tendency that is not affected by extreme values.
Q: Can a data set have multiple modes?
A: Yes, a data set can have multiple modes. If there are two or more values with the same highest frequency, the data set is multimodal. If all values occur with the same frequency, there is no mode.
Q: Which measure of central tendency is the best representation of the data set?
A: The choice of measure depends on the characteristics of the data set and the specific requirements of the analysis. There is no single “best” measure of central tendency. It is important to consider the nature of the data and the research objectives when selecting a measure.
Q: How do I calculate the range of a data set?
A: The range is calculated by subtracting the lowest value from the highest value in a data set. It provides a measure of the spread or variability of the data.
These frequently asked questions provide answers to common queries about mean, median, and mode. Understanding these concepts and their applications helps in effectively analyzing and interpreting data sets.
Examples on Mean, Median, and Mode
Let’s go through some examples to illustrate the calculations of mean, median, and mode.
Example 1: Consider a data set of test scores: 80, 90, 70, 85, 95. Let’s calculate the mean, median, and mode.
To find the mean, add up all the values and divide by the total number of values: Mean = (80 + 90 + 70 + 85 + 95) / 5 = 420 / 5 = 84.
To find the median, arrange the values in ascending order: 70, 80, 85, 90, 95. Since there are five values, the median is the middle value, which is 85.
Since all values occur only once, there is no mode in this data set.
Therefore, the mean is 84, the median is 85, and there is no mode.
Example 2: Consider a data set of test scores: 80, 90, 70, 85, 90. Let’s calculate the mean, median, and mode.
To find the mean, add up all the values and divide by the total number of values: Mean = (80 + 90 + 70 + 85 + 90) / 5 = 415 / 5 = 83.
To find the median, arrange the values in ascending order: 70, 80, 85, 90, 90. Since there are five values, the median is the middle value, which is 85.
Since the value 90 appears twice, it is the mode of this data set.
Therefore, the mean is 83, the median is 85, and the mode is 90.
These examples demonstrate the calculations of mean, median, and mode for different data sets. These measures provide valuable insights into the central tendency of the data and help in analyzing and interpreting the data effectively.
How Kunduz Can Help You Learn Mean, Median, and Mode?
At Kunduz, we understand the importance of mastering concepts like mean, median, and mode. We offer a comprehensive range of educational resources, including tutorials, practice problems, and interactive exercises, to help you learn and understand these concepts.
Our online platform provides a user-friendly interface that allows you to explore and practice mean, median, and mode at your own pace. Our step-by-step explanations and real-life examples make learning engaging and enjoyable.
Whether you’re a student looking to improve your math skills or a professional seeking to enhance your statistical analysis abilities, Kunduz is your go-to resource. We are committed to providing high-quality educational content that empowers learners to excel in their studies and beyond.
Visit Kunduz today and embark on your journey to master mean, median, and mode. Let us guide you towards a deeper understanding of these essential concepts in statistics.
