In mathematics, the midpoint formula plays a crucial role in finding the point that lies halfway between two given points on a line segment. This formula is widely used in various fields, including geometry, economics, and physics. Understanding the concept of midpoint and how to calculate it using the midpoint formula is essential for solving problems related to coordinate geometry.
What is the Midpoint?
The midpoint refers to the center point of a line segment. It is the point that divides the line segment into two equal parts. In other words, the midpoint is equidistant from both endpoints of the line segment. This property makes the midpoint an essential point of reference when analyzing and working with line segments.
What is the Midpoint of a Line?
The midpoint of a line can be visualized as the point that lies exactly in the middle of the line. It is the point where the line can be bisected into two equal halves. This concept is particularly useful when studying and analyzing geometric shapes and their properties.
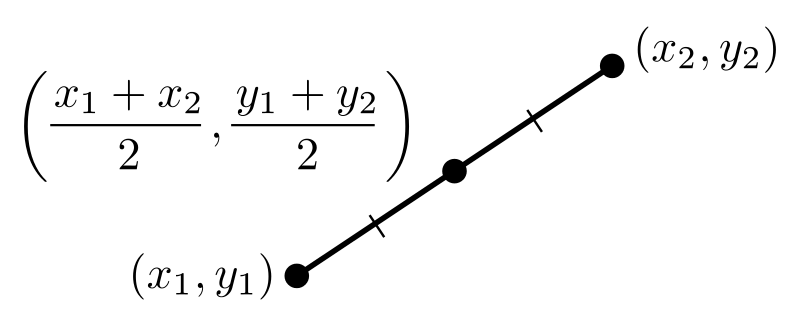
What is the Midpoint Formula?
The midpoint formula is a mathematical tool used to find the exact center point of a line segment. Given any two points, say A and C, the midpoint is a point B which is located halfway between points A and C.
The formula to find the midpoint of a line segment between two points (x1, y1) and (x2, y2) in a coordinate plane is:
M(x, y) = ((x1 + x2)/2, (y1 + y2)/2)
Midpoint Formula in Math
To better understand the midpoint formula, let’s break it down step by step. First, we need to find the average of the x-coordinates of the two given points. This gives us the x-coordinate of the midpoint. Next, we find the average of the y-coordinates of the two points to determine the y-coordinate of the midpoint. By combining these coordinates, we can calculate the exact midpoint of the line segment.
Derivation of Midpoint Formula
The midpoint formula can be derived by considering the concept of averaging the coordinates of two points. By taking the average of the x-coordinates and y-coordinates separately, we can determine the coordinates of the midpoint. This method ensures that the midpoint lies exactly halfway between the two given points.
How to Find a Midpoint?
To find the midpoint between two given points using the midpoint formula, follow these steps:
Step 1: Identify the coordinates of the two given points, which we’ll call (x1, y1) and (x2, y2).
Step 2: Apply the midpoint formula, plugging in the values of the coordinates into the formula.
Step 3: Simplify the formula by performing the necessary calculations.
Step 4: The result will give you the coordinates of the midpoint, which we’ll call (x, y).
By following these steps, you can easily find the midpoint between any two given points on a line segment.
Riemann Sums
In calculus, the midpoint formula is also used in the context of Riemann sums. Riemann sums are a method for approximating the area under a curve. By dividing the interval into smaller subintervals and using the midpoint formula to find the height of each rectangle, the Riemann sum provides an estimate of the area. This technique is widely used in integral calculus to solve various problems.
Formulas Related to Midpoint
The midpoint formula is closely related to other formulas in mathematics. Two notable formulas are the centroid of a triangle formula and the section formula.
Centroid of a Triangle Formula
The centroid of a triangle is the point of intersection of the medians of a triangle. The median is a line joining the vertex to the midpoint of the opposite side of the triangle. The centroid divides the median of the triangle in the ratio 2:1.
Section Formula
The section formula is beneficial to locate the coordinates of a point that divides a line segment joining two points in a given ratio. The point can be located between the points, or anywhere beyond the points, but on the same line.
How do you apply the Midpoint Formula?
To apply the midpoint formula, follow these steps:
Step 1: Identify the coordinates of the two endpoints of the line segment.
Step 2: Plug the values of the coordinates into the midpoint formula.
Step 3: Calculate the midpoint by evaluating the formula.
By following these steps, you can easily apply the midpoint formula to find the coordinates of the midpoint between two given points.
How to Calculate the Midpoint
To calculate the midpoint between two given points using the midpoint formula, follow these steps:
Step 1: Identify the coordinates of the two given points, which we’ll call (x1, y1) and (x2, y2).
Step 2: Plug the values of the coordinates into the midpoint formula.
Step 3: Simplify the formula by performing the necessary calculations.
Step 4: The result will give you the coordinates of the midpoint, which we’ll call (x, y).
By following these steps, you can easily calculate the midpoint between any two given points on a line segment.
Midpoint and Endpoint
The midpoint formula also allows us to find the coordinates of an endpoint if we know the coordinates of the other endpoint and the midpoint. This is particularly useful when working with line segments and trying to determine the missing endpoint.
To find the coordinates of the missing endpoint, follow these steps:
Step 1: Identify the coordinates of the known endpoint, which we’ll call (x1, y1), and the coordinates of the midpoint, which we’ll call (xM, yM).
Step 2: Plug the values of the known endpoint and the midpoint into the midpoint formula.
Step 3: Simplify the formula by performing the necessary calculations to solve for the missing endpoint.
By following these steps, you can find the coordinates of the missing endpoint using the midpoint formula.
How to Calculate Distance Between 2 Points
The distance between two points can be calculated using the distance formula:
d = √[(x2 – x1)² + (y2 – y1)²]
The formula is derived from the Pythagorean theorem, solving for the length of the hypotenuse.
Distance & Midpoint Formula Equation
The distance formula and the midpoint formula are closely related. They both involve the coordinates of two points and provide a way to calculate properties of a line segment.
The distance formula allows us to find the length of a line segment between two points, while the midpoint formula enables us to find the point that lies exactly halfway between the two given points.
By using these formulas, you can analyze and solve problems related to line segments, distances, and coordinates in various fields of mathematics and physics.
Midpoint of a Diagonal Line Example
In the case of a diagonal line segment, the midpoint formula is used to calculate the point that is equidistant from two given points on the line segment. This involves averaging the x and y coordinates of the two points.
Midpoint Method Formula in Economics
In economics, the midpoint method formula is used to calculate the price elasticity of demand. It is a method of calculating percentages using the midpoint between the initial and the final values, rather than the initial values.
Solved Examples on How to Use the Midpoint Formula
Example 1: Find the midpoint of the line segment joining the points (2, 4) and (-6, 8).
To find the midpoint, we apply the midpoint formula:

In this case, (x1, y1) = (2, 4) and (x2, y2) = (-6, 8). Plugging these values into the formula:

Simplifying the formula:

[ M(x, y) = (-2, 6) ]
Therefore, the midpoint of the line segment is (-2, 6).
Example 2: Find the missing endpoint of the line segment if the midpoint is (3, -1) and the other endpoint is (1, 5).
To find the missing endpoint, we apply the midpoint formula:

In this case, (xM, yM) = (3, -1) and (x1, y1) = (1, 5). Plugging these values into the formula:

Simplifying the formula:

Solving these equations, we find:
[ x2 = 5 ]
[ y2 = -7 ]
Therefore, the missing endpoint of the line segment is (5, -7).
How Kunduz Can Help You Learn Midpoint Formula?
At Kunduz, we understand the importance of mastering mathematical concepts like the midpoint formula. That’s why we offer comprehensive resources and personalized tutoring to help students excel in their math studies. Our experienced tutors are passionate about teaching and are dedicated to providing clear explanations and step-by-step guidance.
Whether you’re struggling with understanding the concept of midpoint or need assistance with solving complex problems using the midpoint formula, Kunduz is here to help. Our tutors will work closely with you, providing personalized support to ensure your success.
With Kunduz, learning the midpoint formula becomes an engaging and empowering experience. We believe that every student has the potential to excel in math, and our goal is to unlock that potential through personalized instruction and support.
Don’t let the midpoint formula intimidate you. Join Kunduz today and start your journey towards math mastery!
